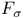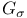Авторизация
Поиск по указателям
Goffman C., Nishiura T., Waterman D. — Homeomorphisms in Analysis
Обсудите книгу на научном форуме Нашли опечатку?
Название: Homeomorphisms in AnalysisАвторы: Goffman C., Nishiura T., Waterman D.Аннотация: This book features the interplay of two main branches of mathematics: topology and real analysis. The material of the book is largely contained in the research publications of the authors and their students from the past 50 years. Parts of analysis are touched upon in a unique way, for example, Lebesgue measurability, Baire classes of functions, differentiability, $C^n$ and $C^{\infty}$ functions, the Blumberg theorem, bounded variation in the sense of Cesari, and various theorems on Fourier series and generalized bounded variation of a function.
Язык: Рубрика: Математика /Анализ /Продвинутый анализ /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1998Количество страниц: 216Добавлена в каталог: 02.04.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Absolute essential supremum of f (ab. ess. supf) 160 161 Absolute measure 20 159 Alexander’s horned sphere 80 Antoine’s necklace 80 84 Approximation 78 Approximation, 78 79 Approximation, interpolation in measure 85 87 Area (nonparametric) 68 203 205 Area (nonparametric), area of f 69 Area (nonparametric), elementary area of g 68 Area (nonparametric), integral formula 68 Avdispahic 167 172 Avdispahic (theorem) 174 Baernstein 173 Baernstein — Waterman (theorem) 150 Baernstein, Waterman 152 Baire category theorem 187 Baire space 9 16 103 187 Banach 100 175 Banach Indicatrix Theorem 193 Bary 131 Berman, Brown, Cohn 49 Besicovitch 84 199 Bi-Lipschitzian 8 61 63 67 68 190 Bitopology 10 Blumberg 77 Blumberg (theorem) 9 99 104 Blumberg, property 9 104 Blumberg, set 106 Blumberg, set, simultaneous 106 108 Blumberg, set, strong 107 Blumberg, space 103 104 Bradford — Goffman (theorem) 9 99 Breckenridge, Nishiura 39 Brouwer 192 Bruckner (theorems) 8 38 Bruckner — Davies — Goffman (theorem) 17 20 Bruckner — Goffman (theorems) 21 29 Buczolich (theorem) 9 190 Category, almost continuous at x 100 Category, homogeneous second 99 102 Category, relative to E, first 99 Category, relative to E, heavy 100 Category, relative to E, second 99 100 Cell, projecting n-cell 81 Cell, topological n-cell 81 89 91 94 Cesari 38 39 70 176 177 Chanturiya (theorem) 174 Circle group $(T = \mathbb{R}/\pi\mathbb{Z}) 111 Completely metrizable space 187 188 Condition GW ((h)) 138—141 150 Condition UGW 149 150 152 153 Continuum Hypothesis 104 160 Convolution function 112 Convolution measure 127 Darboux property 41 56 Davenport (lemma) 124 Deformation 90—92 95 96 Deformation, capture 93 Deformation, precise partition 93 Denjoy property 43 47 density 189 Density topology 5 23 24 63 189 195 196 Density topology 8 9 104 Density-closure 8 195 Density-interior 8 Direction 90 93 Dirichlet kernel 112 Dirichlet — Jordan theorem 113 114 119 131 distribution 65 Distribution, n variables 70 Distribution, n variables, function 70 Distribution, n variables, measure 71 Distribution, n variables, measure representation of partial derivative 71 Distribution, n variables, partial derivative 71 Distribution, one variable, derivative 66 205 Distribution, one variable, function 66 205 Distribution, one variable, measure 66 Distribution, one variable, measure representation of derivative 66 Essential absolute continuity 67 Essential derivative 67 Essential length 65 Essential variation 65 67 194 195 Evans, Gariepy 206 Falconer 199 Federer 188 Fejer 117 Fejer — Lebesgue theorem 112 113 117 Fourier, 136 154 Fourier, coefficients 111 172 174 Fourier, conjugate, function 121 Fourier, conjugate, series 120 Fourier, modified partial sum 116 Fourier, multiple 177 Fourier, partial sum 111 Fourier, series (S(f), S(x;f)) 111 Frechet 205 Frechet (theorem) 205 Frechet equivalence 38 Function, n variables, approximately continuous 189 195 Function, n variables, Borel measurable 188 Function, n variables, linearly absolutely continuous (= absolutely continuous) 70 Function, n variables, linearly continuous 70 Function, n variables, Lipschitzian 68 69 Function, one variable, 15 159 Function, one variable, 172 174 Function, one variable, absolutely continuous 62 64 193 Function, one variable, absolutely essentially bounded 20 160 161 163 180 Function, one variable, absolutely GW 164 Function, one variable, absolutely integrable 160 161 183 Function, one variable, absolutely measurable 159 Function, one variable, absolutely regulated 162—164 183 Function, one variable, approximate derivative 54 Function, one variable, approximately continuous 23 25 62 63 Function, one variable, approximately differentiate 78 Function, one variable, Borel measurable 188 Function, one variable, bounded deviation 178 Function, one variable, bounded variation 192 Function, one variable, generalized bounded variation 167 Function, one variable, indicatrix 131 174 194 195 Function, one variable, Lipschitzian 63 Function, one variable, quasi-continuous 104 106—108 Function, one variable, regulated 194 Function, one variable, simple 14 Function, one variable, variation 21 Functions, 159 Functions, absolutely equivalent 159 162 178 Functions, classes of, 175 Functions, classes of, 175 Functions, classes of, 15 Functions, classes of, Baire 188 Functions, classes of, Baire, class 0 188 Functions, classes of, Baire, class 1 188 198 Functions, classes of, Baire, class 2 188 Functions, classes of, Borel class 1 197 198 Functions, classes of, Borel measurable 188 Functions, classes of, bounded variation (BV) 192 194 Functions, classes of, bounded variation, Cesari (BVC) 70 71 176 206 Functions, classes of, continuous, bounded variation (CBV) 21 193 Functions, classes of, Darboux, Baire class 1 41—43 45 47 Functions, classes of, differentiate, infinitely 35 Functions, classes of, differentiate, n-times continuously 30 Functions, classes of, generalized bounded variation, 177 Functions, classes of, generalized bounded variation, 176 177 Functions, classes of, generalized bounded variation, 172—174 Functions, classes of, generalized bounded variation, 167 171 Functions, classes of, generalized bounded variation, harmonic bounded variation (HBV) 168—171 173—175 177 Functions, classes of, generalized bounded variation, V[h] 173 178 Functions, classes of, GW 169 Functions, classes of, Lipschitz class 114 Functions, classes of, regulated (R(T)) 113 136 138 139 141 175 Functions, classes of, UGW 169 Functions, classes of, Zahorski 41 42 Functions, classes of, Zahorski 41 42 Functions, complementary 173 176 Garsia, Sawyer 175 Gleyzal 44 Gleyzal (theorem) 44 54 Goffman 70 78 80 88 168—170 173 176 Goffman (theorems) 71 79 83 84 86—88 Goffman — Liu (theorem) 71 Goffman — Neugebauer (theorem) 56 Goffman — Waterman (theorems) 138 177 196 Goffman, Neugebauer, Nishiura 195 Goffman, Pedrick 97 Goffman, Waterman 77 117 196 198 Goffman, Zink 77 Gorman, decomposition 5 Gorman, example 19 Gorman, sequence 5 Gorman, theorem 7 14 20 hadamard 178 Hardy 122 Haupt, Pauc 195 Hausdorff dimension, 199 Hausdorff measure 68 97 104 Hausdorff measure, 30 Hausdorff measure, 71 Hausdorff measure, 71 199 Hausdorff measure, 199 Hausdorff measure, 198 Hausdorff measure, counting 199 Hausdorff measure, outer 199 Hausdorff naive packing, 30 Hausdorff naive packing, 200 Hausdorff naive packing, 37 38 Hausdorff naive packing, 200 Hausdorff naive packing, 30 Hausdorff naive packing, 199 Hausdorff naive packing, 200 Hausdorff naive packing, rarefaction index 202 Hilbert transform (H[f]) 122 Homotopy 89 94 95 98 Integral formula, area 68 69 Integral formula, length 63 64 Integral mean value theorem 141 Interval function 44 47 54 Interval function (convergence of) 44 Interval function f([a, b]) = f(b) — f(a) 131 138 Jacobian (J(h, x)) 68 JORDAN 64 Jordan — Schoenflies (theorem) 80 81 84 Jurkat — Waterman (theorems) 121 Jurkat, Waterman 120 124 Kahane — Katznelson (theorem) 117 Kahane, Katznelson 117 124 Kahane, Zygmund 131 Laczkovich — Preiss (theorem) 31 37 Lebesgue ix 68 204 Lebesgue equivalence 3 21 65 Length (nonparametric) 63 203 Length (nonparametric), elementary length of g 63 203 Length (nonparametric), essential length of f (ess l(f, [0,1])) 63 203 length Levy 103 Lower semicontinuous functional 64 Lower semicontinuous functional of n variables functions, area 69 Lower semicontinuous functional of n variables functions, elementary area 69 204 Lower semicontinuous functional of n variables functions, variation 69 Lower semicontinuous of one variable functions, elementary length 64 204 Lower semicontinuous of one variable functions, essential variation 194 Lower semicontinuous of one variable functions, length 64 Lower semicontinuous of one variable functions, total variation 64 193 Lukes, Maly, Zajicek 10 Lusin (theorem) 77 78 84 86 104 Map, approximately continuous 197 Map, bi-Lipschitzian 189 190 Map, dilation 190 Map, Lipschitzian 189 190 199 Map, Lipschitzian, constant of f (Lip(f)) 189 Maps, classes of, bimeasurable 85—87 Maps, classes of, bimeasurable 85 Maps, classes of, self-homeomorphism (H[In]) 85—87 Maximoff (theorem) 41 56 Mean, (C,l) 112 Mean, Abel 113 121 Measurable boundary (upper, lower) 78 Measure, 95 Measure, equivalence 43 Measure, Lebesgue equivalence 89 98 Measure, Lebesgue — Stieltjes 91 Measure, Lebesgue-like 43 46 47 89 90 93 95 Measure, positive 43 Modulus of continuity 114 Modulus of continuity, integral 115 Neugebauer 43 57 104 106 Neugebauer (theorems) 45 46 108 Olevskii (theorem) 124 129 Oniani 121 Oscillation of f on E (osc(f; ?)) 162 Oskolkov 173 Oxtoby 15 20 97 160 Oxtoby, Ulam 97 Pal — Bohr theorem xii 111 117 120 121 Partition, boundary collection 94 Partition, mesh 94 Partition, n-cell 94 Partition, precise partition 95 Pierce — Waterman theorem 139 Point of almost continuity see “Category almost Point of almost continuity, density 8 63 189 190 195 Point of almost continuity, dispersion 8 63 189 190 Point of almost continuity, varying monotonicity 27 Preiss 41 47 56 Preiss (theorem) 43 Prus — Wisniowski 176 Radon — Nykodym derivative 67 Rarefaction index 202 Rarefaction index, 36 Representation 38 Riemann localization principle 177 Riemann mapping theorem 117 122 Riesz, F. and M. 122 Rogers 198 Saakyan 117 121 Saks — Sierpiriski (theorem) 77 78 Salem 117 131 Salem, theorem 132 Schramm, Waterman 172 Schwarz, example 203 Selection 43 46 47 Set, 103 Set, 15 159 Set, 15 159 Set, absolutely measurable 159 Set, analytic (= Suslin) 3 15 188 Set, Blumberg see “Blumberg set” Set, Borel, 188 195 Set, Borel, 188 Set, c-set 5 Set, closure of 187 Set, connected 196 Set, continuity set of f (C(f)) 106 Set, cozero-set 195 Set, density-closed 195 Set, density-open 5 195 Set, homogeneous second category 99 Set, hyper plane 90 91 Set, interior of 187 Set, k-flat 90 Set, porous 4 62 189
Реклама
 |
|
О проекте
|
|
О проекте



 -approximation in measure
-approximation in measure 











 ,
, 





 -absolutely measurable
-absolutely measurable  -bounded variation (
-bounded variation (




![$(C^{\infty}[0,1])$](/math_tex/a7409d539e4cee762917762aeac014a282.gif)
![$(C^n[0,1])$](/math_tex/a4f347285db3df6e4698a05df0c80cd182.gif)



 -bounded variation (ABV)
-bounded variation (ABV) 


![$H_1(v_f[K_f])$](/math_tex/24ab7e32bbc8a9f01fb3e25362c79e9682.gif)



 -cover
-cover ![$npH_1(v_f[K_f])$](/math_tex/02a4f32baaf580ae48a8ca42dfa7c2f582.gif)

![$npH_{\alpha}(v_f[K_f])$](/math_tex/5c90b17c6c8817e41db9773b998ca14a82.gif)

![$npH_{\frac1n}(v_f[K_f])$](/math_tex/e0407f3ec50beea7a6d538ff043d75df82.gif)


![$(E_1(g, [0,1]))$](/math_tex/14634cec1a6dc7f198066813503e46d882.gif)

![$(\mathcal{M}[I^n,I^m])$](/math_tex/89ccb5a68ff257eb2e1ea30e37c05eed82.gif)
 -admissible
-admissible 


![$\Lambda(v_f,[K_f])$](/math_tex/f6b871510ed7164e888bbf455da2351282.gif)
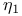 -set
-set