|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hewitt E., Ross K.A. — Abstract Harmonic Analysis (Vol. 2) |
|
|
 |
| Предметный указатель |
Measure(s), total variation of 169 I
Mela, J. F. 576
mesh 13 I
Metrizability of topological groups 70 I
Meyer, Y. 547 603 605
Milnor, J. W. 207
Minimal divisible extension of a group 419 I 445—447
Minkowski’s inequality 138 I
Mirkil, H. 603
Modular function 196 I
Modular function for 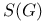 438 I 438 I
Modular function on closed normal subgroups 206 I
Monothetic group 85 I 390 407—409
Monothetic group, generators of 105 I 407 415
Monothetic group, largest 407 I
Monothetic semigroups 105 I
Moore, J. C. 208
Morgenthaler, G. W. 446
Mostow, G. D. 198 205 207
Mrowka, S. 99
Multilinear mapping 722
Multinomial coefficient 117
Multiplicative function 345 I
Multiplicative linear functional 474 I
Multiplicity of family of sets 15 I
Multiplicity of representations 18
Multipliers 368
Multipliers, isometric 389
Multipliers, table of 410—411
Murakami, S. 60
Murnaghan, F. D. 155
Mycielski, J. 69
n-dimensional space 3 I 15
Nagumo, M. 518
Naimark, M. A. 154 207 251 252 290 325 326 327 495 520
Nakamura, M. 325
Nakayama, T. 113 208 483
Namioka, I. 710
Narrow topology 549
Natural mapping 4 I
Neighborhood (always open) 9 I
Net 14 I
Neumann, J. von 60 113 114 290 312 322 323 326 366 518 549 574 680 693
Noble, M. E. 448
Nondiscrete topologies for Abelian groups 27 I
Nondiscrete topologies for Z 27 I
Nonmeasurable sets 226 I
Nonnegative linear functional 461 I
Nonnegative linear functional on 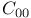 120 I 120 I
Nonnormal groups 74—76 I
Norm 453 I
Norm in 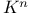 3 I 3 I
Norm in 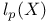 3 I 3 I
Norm in  135 I 135 I
Norm of linear function 454 I
Norm of multilinear mapping 722
Norm topology 454 I
Norm, 703
Norm, uniform 119 I 230
Normal algebra 484
Normal family of functions 495
Normal operator 467 I
Normal operator, existence of inverse 484 I
Normal subgroup 16 I
Normal topological group 16 I
Normality of locally compact groups 761
Normed  -algebra 313 I -algebra 313 I
Normed A -module 263
Normed algebra 469 I
Normed linear space 453 I
Normed linear space, reflexive 457 I
Normed linear space, weak topology 458 I
Normed linear space, weak-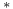 topology 458 I topology 458 I
Nowhere dense 456 I
Null function 124 I
Null set 124 I
Nyman, B. 521
Oberhettinger, F. 214
One-parameter subgroup 85 I
Open and closed subgroup 33—34 I 62
Open mapping theorems 710
Operations  180 180
Operators 452 I
Operators, adjoint 466 I
Operators, direct sum of 688
Operators, Hermitian 467 I
Operators, normal 467 I
Operators, positive-definite 467 I
Operators, projection 467 I
Operators, sublinear 631
Operators, sum of 468 I
Operators, unitary 467 I
Orbit 46 311
Ordered groups 24 I
Orlicz, W. 413
Orthogonal elements 465 I
Orthogonal group 7 I (see also “\mathfrak{D}(n)$”)
Orthogonal group, special 7 I (see also ““\mathfrak{S}\mathfrak{D}(n)$”)
Orthogonal matrix 7 I
Orthogonal set 465 I
Orthogonal sets 465 I
Orthogonality relations in 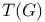 8 11 14 8 11 14
Orthonormal basis 465 I
Orthonormal set 465 I
Ovaert, J.-L. 290
p-adic integers 109 I (see also “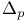 ”) ”)
p-adic number field 112 I (see also “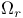 ”) ”)
p-adic numbers 109 I (see also “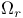 ”) ”)
p-primary group 439 I
p-rank of a group 444 I
P-topology 361 I
Paley, R. E. A. C. 413 414
Paracompact space 13 I
Paracompactness of locally compact groups 76 I
Parker, W. A. 448
Parseval, M. A. 250
Parseval’s identity 226
Parseval’s identity, generalizations 249
Partition of a set 2 I
Partitions of unity 9 —10 I 495
Permutation group 8 I
permutations 8 I
Permutations, transitive 46
Peter — Weyl theorem 24 81
Peter, F. 60 114 366 548
Phillips, K. L. 679
Phillips, R. S. 327
Pitt, H. R. 511 519 520 574
Pitt’s Tauberian theorems 511
Plancherel, M. 251 252
Plancherel’s theorem 226
Poisson summation formula 246
Pollard, H. 549 550
Pontryagin — van Kampen duality theorem 378 I
Pontryagin — van Kampen duality theorem, uniqueness of T 424 I
Positive functionals 316 I
Positive functionals on 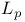 357 357
Positive functionals, continuity of 270 274
Positive functionals, discontinuous 357
Positive functionals, extensible 317 I
Positive functionals, nonextensible 331 I
Positive linear functional, strictly 461 I
Positive-definite functions 253 161
Positive-definite functions, 1-integrally 275
Positive-definite functions, decomposition theorem 260
Positive-definite functions, extensions 363
Positive-definite functions, p-integrally 290
Positive-definite functions, pointwise limits of 280 288 301 302
Positive-definite matrix 683
Positive-definite operator 467 I
| Positive-definite operator, spectrum is nonnegative 484 I
Positive-definite operator, square root of 485 I 691
Pospisil, B. 99
POVZNER, A. 251 325 550
primary group 439 I
Product of characters 355 I
Product of complex measures 182 I
Product of functionals 152 I 159
Product of groups 6 I
Product of measures 1 52 I
Product of sets 2—3 I
Product of topological groups 52 I
Product of topological groups, character group of 362—365 I
Projection 54 I
Projection operator 467 I
Projection-valued measure 316
Projective limit 56 I
Projective limit, compact groups 102
Proper ideal of an algebra 469 I
Proper subgroup 4 I
Property 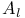 480 480
Property  481 481
Pseudomeasures 361
Pure independent set 448 I
Pure subgroups 447 I 395
Purely discontinuous measure 269 I
Quasi-inverses 471 I
Quasi-inverses, form open set 472 I
Quaternion group 52 (see also “Generalized quaternion group  ”) ”)
Quaternions of norm 1 I52
Quaternions, Haar measure on 210 I
Quotient group 4 I 40
Quotient group, character group of 365 I
Quotient space 4 I 452
Quotient space, homogeneity of 37 I
Quotient space, topology of 36 I
r-adic integers 109 I (see also “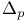 ”) ”)
r-adic numbers 109 I (see also “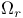 ”) ”)
r-iold transitive 46
RAAA preface
Radon — Nikodym theorem 144 I
Raikov, D. A. 289 290 291 325
Rajagopalan, M. 448 469
Rank of a group 444 I
Rao, M. M. 252
Real algebra 469 I
Real characters 390 I 393
Real characters, extensibility of 391 I
Real linear space 452 I
Real matrix 7 I
Real n-dimensional space 3 I
Real-character group 390 I
Reduce 323 I
Reduced group 440 I
Reduced word 8 I
Reducible representation 323 I
Reducible set of operators 323 I
refinement 13 I
Reflexive space 457 I
Regular algebra 484
Regular ideal 475 I
Regular left ideal 474 I
Regular measure 127 I
Regular representation 342 I 36 58 473
Regular topological space 9 I
Reiner, I. 103
Reiter, H. J. 327 433 517 520 533 539
Reiter’s theorem 529
Relatively bounded linear functional 461 I
Relatively invariant functionals 203 I
Relatively invariant functionals, examples 212 I
Representation space 312 I
Representation(s) of a group 312 I
Representation(s) of a semigroup 312 I
Representation(s) of an algebra 312 I
Representation(s) of an algebra with unit 313 I
Representation(s) of finite groups 47
Representation(s), character of 13
Representation(s), conjugate 17 58
Representation(s), contained in 18
Representation(s), continuous 341 I
Representation(s), cyclic 315 I
Representation(s), decomposition of 19
Representation(s), direct sum of 18
Representation(s), equivalent 314 I 2
Representation(s), extension of 29
Representation(s), identity 3
Representation(s), invariant subspace under 312 I
Representation(s), irreducible 323 I
Representation(s), multiplicity 18
Representation(s), reducible 323 I
Representation(s), regular 342 I 36 58 473
Representation(s), restriction of 29
Representation(s), strongly continuous 335 I
Representation(s), sufficiently many 343 I
Representation(s), summand of 18
Representation(s), tensor product of 20
Representation(s), weakly continuous 335 I
Representation(s), weakly measurable 335 I
Representative functions 5
Restriction algebra 485
Restriction of representations 29
Richards, I. 602
Rickert, N. W. 291 469 567
Rider, D. 147 152 153 414 415 442 447 448
Rieffel, M. A. 287 290 414
Riemann — Lebesgue lemma 81
Riesz products 426 448
Riesz — Thorin convexity theorem 722
Riesz — Thorin convexity theorem, applied 76 226—228
Riesz, F. 251 252 290 325 326 445 448
Riesz, M. 252 413
Right Haar integral 195 I (see also “Left Haar integral”)
Right Haar measure 195 I (see also “Left Haar measure”)
Right unit relative to I 474 —475 I (see also “Left unit relative to I”)
Ring of sets 118 I
Rolewicz, S. 576
Rosenthal, H. P. 437 576 604 605
Ross, K. A. 208 291 629 679
Rudin — Shapiro polynomials 429
Rudin, W. 238 250 251 252 253 290 326 327 429 437 446 447 448 513 533 548 552 570 574 576 602 603
Ryll — Nardzewski, C. 576
Saeki, S. 516 601
Sakai, S. 415
Saks, S. 218
Salem, R. 290 446 551 575 576 603 604
Sankaran, S. 325
Sapiro, Z. Ya. 154
Scalar field 452 I
Schatten, R. 113 683
Schoenberg, I. J. 327
Schur, I. 59 60 153 289 483
Schur’s lemma 6
Schwartz, J. T. 114 153 543
Schwartz, L. 253 533 551 602 603
Schwartz’s example 533
Schwarz’s inequality 464 I
Second category 456 I
Second character group 376 I
Second isomorphism theorem for groups 51
Second isomorphism theorem for topological groups 45 I
Sections 153 I
Segal, I. E. 60 114 290 430 447 483 521 548 602
Self-dual groups 422 I
Self-representation 47 115
Semicharacter 345 I
Semicontinuous functions 121 I
Semidirect product of groups 6—7 I
Semidirect product of topological groups 58 —59 I
Semidirect product, Haar measure on 210 I
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



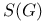
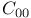
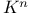
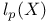

 -algebra
-algebra 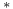 topology
topology 
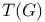
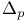 ”)
”)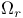 ”)
”)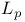
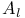

 ”)
”)