|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hewitt E., Ross K.A. — Abstract Harmonic Analysis (Vol. 2) |
|
|
 |
| Предметный указатель |
 -set 552 -set 552
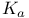 -set 552 -set 552
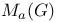 269 I (see also “ 269 I (see also “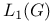 ”) ”)
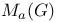 , isomorphic with , isomorphic with 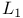 272 I 272 I
 -mesh 13 I -mesh 13 I
 -topology 360 I -topology 360 I
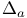 109 I 416—417 109 I 416—417
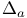 , character group of 402 I , character group of 402 I
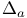 , Haar measure on 202 I , Haar measure on 202 I
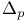 109 I 109 I
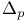 , automorphism group of 434 I , automorphism group of 434 I
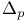 , minimal divisible extension of 419 I , minimal divisible extension of 419 I
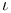 -almost everywhere 124 I -almost everywhere 124 I
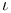 -measurable function 125 I -measurable function 125 I
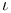 -measurable set 125 I -measurable set 125 I
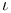 -null function 124 I -null function 124 I
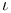 -null set 124 I -null set 124 I
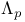 set 420 set 420
 (rational numbers) 3 I (rational numbers) 3 I
 , character group of 404 I 414 , character group of 404 I 414
 (real line) 3 I (real line) 3 I
 is open continuous homomorph of totally disconnected group 50 I is open continuous homomorph of totally disconnected group 50 I
 , automorphism group of 433 I , automorphism group of 433 I
 , character group is R 367 I , character group is R 367 I
 , compact connected topology for 415 I , compact connected topology for 415 I
 , continuous homomorphisms of 370 I , continuous homomorphisms of 370 I
 , Haar measure on 198 I , Haar measure on 198 I
 , invariant mean for , invariant mean for 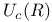 256 I 256 I
 , invariant means for , invariant means for 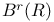 240 I 240 I
 , topologies in 27 I , topologies in 27 I
 3 I 3 I
 , automorphism group of 434 I , automorphism group of 434 I
 , characterized 104 I , characterized 104 I
 , closed subgroups of 92 I , closed subgroups of 92 I
 (integers) 3 I (integers) 3 I
 , character group is T 366 I , character group is T 366 I
 , invariant mean for , invariant mean for 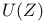 256 I 256 I
 , nondiscrete topology for 27 I , nondiscrete topology for 27 I
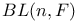 7 I 7 I
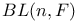 has inequivalent uniform structures 28—29 I has inequivalent uniform structures 28—29 I
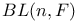 is locally Euclidean 29—31 I is locally Euclidean 29—31 I
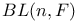 , Haar measure on 201 I 209 , Haar measure on 201 I 209
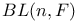 , left invariant metric on 78 I , left invariant metric on 78 I
 , representations of 151 , representations of 151
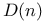 7 I 7 I
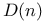 is compact 29 I is compact 29 I
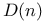 is locally Euclidean 29—31 I is locally Euclidean 29—31 I
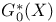 as convolution algebra 265 I as convolution algebra 265 I
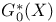 , adjoint operation in 299 I , adjoint operation in 299 I
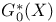 , equivalent with M(G) 269 I , equivalent with M(G) 269 I
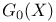 119 I 119 I
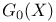 , characterized as Banach algebra 481 I , characterized as Banach algebra 481 I
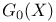 , closed ideals in 483 I , closed ideals in 483 I
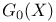 , conjugate space of 170 I 175 , conjugate space of 170 I 175
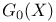 , multiplicative linear functionals of 484 I , multiplicative linear functionals of 484 I
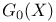 , structure space is X 484 I , structure space is X 484 I
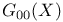 119 I 119 I
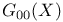 , nonnegative linear functionals on 120 I , nonnegative linear functionals on 120 I
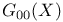 , unbounded linear functionals on 167 I , unbounded linear functionals on 167 I
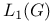 has approximate unit 303 I has approximate unit 303 I
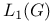 has no unit 303 I has no unit 303 I
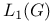 , all , all  -representations 294 -representations 294
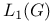 , and , and 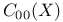 573 573
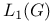 , center of 85 109 , center of 85 109
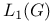 , commutative if and only if G is 302 I , commutative if and only if G is 302 I
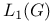 , Ditkin’s condition 501 , Ditkin’s condition 501
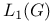 , factorization in 271 515 , factorization in 271 515
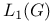 , ideals characterized 303 I , ideals characterized 303 I
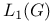 , isomorphic with , isomorphic with 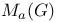 272 I 272 I
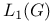 , spectral synthesis fails 597 , spectral synthesis fails 597
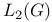 , invariant subspaces 237 , invariant subspaces 237
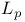 conjecture 469 471 conjecture 469 471
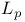 Fourier transform 225 227 Fourier transform 225 227
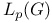 -maximal function 606 607 -maximal function 606 607
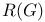 260 330 338 260 330 338
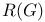 , as convolution algebra 352 , as convolution algebra 352
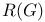 , Ditkin’s condition 344 , Ditkin’s condition 344
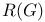 , spectral synthesis fails 597 , spectral synthesis fails 597
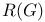 , structure space 340 , structure space 340
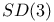 , representations of 136—141 , representations of 136—141
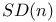 71 71
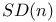 is compact 29 I is compact 29 I
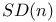 is locally Euclidean 29—31 I is locally Euclidean 29—31 I
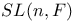 7 I 7 I
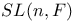 has inequivalent uniform structures 28—29 I has inequivalent uniform structures 28—29 I
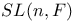 has no finite-dimensional unitary representations 350 I has no finite-dimensional unitary representations 350 I
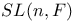 is locally Euclidean 29—31 I is locally Euclidean 29—31 I
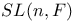 , homomorphisms into , homomorphisms into 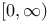 212—213 I 212—213 I
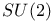 , Haar measure on 134 , Haar measure on 134
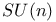 71 71
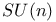 , representations of 125—136 , representations of 125—136
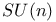 is compact 29 I is compact 29 I
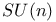 is locally Euclidean 29—31 I is locally Euclidean 29—31 I
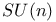 , Hewitt and Ross, Abstract harmonic analysis vol II , Hewitt and Ross, Abstract harmonic analysis vol II
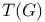 (trigonometric polynomials) 5 211 (trigonometric polynomials) 5 211
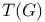 (trigonometric polynomials) is dense in (trigonometric polynomials) is dense in  23 23
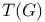 (trigonometric polynomials) is dense in (trigonometric polynomials) is dense in 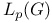 211 211
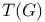 (trigonometric polynomials) is Krein algebra 163 (trigonometric polynomials) is Krein algebra 163
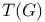 (trigonometric polynomials), invariant subspaces 204 473 (trigonometric polynomials), invariant subspaces 204 473
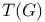 (trigonometric polynomials), linear functionals on 157 161 178—187 (trigonometric polynomials), linear functionals on 157 161 178—187
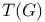 (trigonometric polynomials), orthogonality relations 8 11 14 (trigonometric polynomials), orthogonality relations 8 11 14
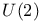 , representations of 150 , representations of 150
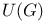 247 I 302 247 I 302
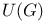 , existence of invariant means 250 I , existence of invariant means 250 I
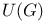 , uniqueness of invariant means 252 I , uniqueness of invariant means 252 I
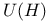 115 (see also “ 115 (see also “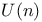 ”) ”)
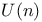 7 I 7 I
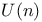 is arcwise connected 64 I is arcwise connected 64 I
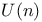 is compact 29 I is compact 29 I
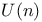 is locally Euclidean 29—31 I is locally Euclidean 29—31 I
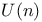 , closed subgroups 101 194 663 , closed subgroups 101 194 663
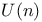 , integrals on 115—124 146 , integrals on 115—124 146
 -functions 259 I -functions 259 I
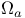 108 I 108 I
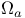 , character group of 400 I , character group of 400 I
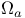 , closed subgroups 116 I , closed subgroups 116 I
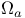 , Haar measure on 202—203 I , Haar measure on 202—203 I
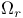 109 I 109 I
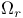 , automorphism group of 433 I , automorphism group of 433 I
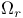 , character group is , character group is 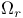 400 I 400 I
 2 (see also “Dual object”) 2 (see also “Dual object”)
 -algebra of sets 118 I -algebra of sets 118 I
 -bounded set 93 -bounded set 93
 -compact spaces 111 -compact spaces 111
 -compact spaces, product of 13 —14 I -compact spaces, product of 13 —14 I
 -finite set function 118 I -finite set function 118 I
 -locally finite 13 I -locally finite 13 I
 -ring of sets 118 I -ring of sets 118 I
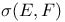 topology 717 topology 717
 -representation 314 I -representation 314 I
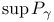 632 632
 -mesh 13 I -mesh 13 I
0-dimensional group, small subgroups of 62 I
0-dimensional space 11 I
a-adic integers 109 I (see also “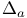 ”) ”)
a-adic numbers 109 I (see also “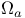 ”) ”)
a-adic solenoid 114 I
Abelian group see “Group”
Abelian group, nondiscrete topologies 27 I
Absolutely continuous measure 180 I 269
Absolutely convergent Fourier series 330
Abstract Tauberian theorem 499
Act disjointedly 719
Additive function 452 I
Adjoint homomorphism 392 I
Adjoint homomorphism, generalized 203
Adjoint in 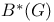 310 I 310 I
Adjoint in 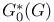 299 I 299 I
Adjoint in 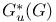 310 I 310 I
Adjoint in an algebra 313 I
| Adjoint in M(G) 300 I
Adjoint operator 466 I 711 712
Agmon, S. 521
Akemann, C. A. 113 414 447
Alaoglu’s theorem 458 I
Algebra 469 I
Algebra of sets 118 I
Algebra with adjoint operation 313 I
Algebra,  -algebra 313 I -algebra 313 I
Algebra, convolution 263 I
Algebra, homomorphism 470 I
Algebra, imbedded in algebra with unit 470 I
Almost everywhere 124 I
Almost periodic compactification 311
Almost periodic function 247 I (see also “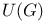 ”) ”)
Alternating group 46
Ambrose, W. 326
Amitsur, A. S. 474
Analytic functions operating in algebras 490 603
Annihilator of 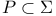 62 62
Annihilator of 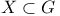 365 I 64 365 I 64
Annihilator, generalized 202
Anti-symmetric tensors 148
Approximate unit 303 I
Approximate unit for 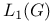 303 I 107 303 I 107
Approximate unit for compact groups 88 273 286 335
Approximate unit for LCA groups 298
Approximate unit, bounded 87
Approximation theorems 431—432 I 435
Arbitrarily small sets 62 I
Arcwise connected space 111
Artin, E. 143
Automorphism group 426—429 I
Automorphism group, examples 433 I
Automorphism group, inner automorphism subgroup 439 I
Automorphism group, modular function of 438 I
Automorphism group, non locally compact 435 I
Automorphism, inner 4 I
Automorphism, topological 426 I 208
Babenko, K. I. 630
Baire category theorem 42 I 456
Baire measurable function 118 I
Baire sets 118 I
Baire sets and Haar measure 280 I
Balanced neighborhood 453 I
Banach  -algebra 313 I -algebra 313 I
Banach A -module 263
Banach algebra 469 I
Banach algebra in  484 484
Banach algebra in 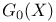 , where X is the structure space 489 , where X is the structure space 489
Banach fields, characterized 473 I
Banach modules in  451 502 451 502
Banach modules in  , spectral synthesis fails 600 , spectral synthesis fails 600
Banach space 455 I
Banach space, reflexive 457 I
Banach space, weak topology 458 I
Banach space, weak-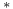 topology 458 I topology 458 I
Banach — Steinhaus theorem 456 I
Banach, S. 435 446 447
Bari, N. K. 250 366
Basis of a group 442 I
Basis of a linear space 681
Basis of a measure space 215 I
Basis, orthonormal 465 I
Belong locally 495
Bernstein, S. 441
Berry, A. C. 251 327
Beurling, A. 519 521 522 549 550 551 601 605
Bieberbach, L. 445
Bilinear functional 453 I
Bilinear functional, bounded 468 I
Bird 210
Birkhoff, G. 6 45 683
Blocks of Krein algebra 162
Bochner, S. 206 250 251 289 325 326 327 413 448 520 549
Bochner’s theorem 293 160
Boerner, H. 153 155
Bohr compactification 430 I 302
Bohr, H. 312 448 519
Boolean  -homomorphism 316 -homomorphism 316
Borel measurable function 118 I
Borel sets 118 I
Boundary 497
Bounded bilinear functional 468 I
Bounded left approximate unit 87 (see also “Approximate unit”)
Bounded linear function 454 I
Bounded linear function, relatively 461 I
Bounded order 439 I
Bounded order, characterized 449 I
Bourbaki, N. 115
Brainerd, B. 414 434
Bunyakovskii’s inequality 137 I
Burckel, R. B. 310 399 726
Burckhardt, H. 250
Burnside, W. 54 59 60 480
Calderon sets 513
Cancellation laws 98—99 I
Cancellation semigroup 258 I
Caratheodory outer measure 123 I
Caratheodory, C. 325
Cardinal number of character groups 382 I 396
Cardinal number of dual objects 43 61 99
Cardinal number of nondiscrete locally compact groups 31 I
Cardinal number, notation for 2 I
Carleman, T. 251 435 520
Carleson set 575
Carleson, L. 574 575
Cartan, E. 153 548
Cartan, H. 250 251 253 309 310 327
Cartesian product of sets 2 I
Category, Baire 456 I
Category, theorem of Baire 42 I 456
Cauchy — Bunyakovskii — Schwarz inequality 464 I
Cauchy’s inequality 137 I
Cayley, A. 156
Cech, E. 99
Center of 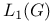 85 109 85 109
Center of a semigroup 84
Center of a topological group 46 I 65 4291
Center of an algebra 84
Central element 84
Central functions 84
Central measures 84
Chandrasekharan, K. 520
Character group 355 I
Character group and structure space of 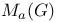 358—361 I 358—361 I
Character group of 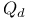 404 I 414 404 I 414
Character group of 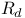 405 I 405 I
Character group of 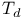 405 I 405 I
Character group of 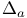 402 I 402 I
Character group of 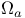 400 I 400 I
Character group of 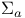 403 I 403 I
Character group of closed subgroup 380 I
Character group of finite group 367 I
Character group of local direct product 373 I
Character group of products 362—365 I
Character group of quotient group 365 I
Character group of R 367 I
Character group of T 366 I
Character group of weak direct product 364 I
Character group of Z 366 I
Character group with only one element 350 I 370
Character group,  -topology of 360 I -topology of 360 I
Character group, P-topology of 361 I
Character group, topologically isomorphic with the group 422 I
Character of a measure space 215 I
Character of a measure space and dimension of 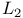 225 I 225 I
Character of a representation 13
Character(s) (of a group) 345 I
Character(s),  -measurable implies continuous 346 I -measurable implies continuous 346 I
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -set
-set 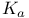 -set
-set 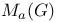
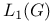 ”)
”)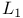
 -mesh
-mesh  -topology
-topology 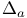
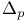
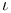 -almost everywhere
-almost everywhere 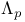 set
set  (rational numbers)
(rational numbers)  (real line)
(real line) 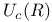
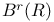

 (integers)
(integers) 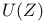
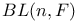
 , representations of
, representations of 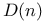
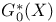 as convolution algebra
as convolution algebra 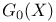
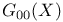
 -representations
-representations 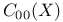
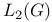 , invariant subspaces
, invariant subspaces 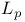 conjecture
conjecture 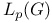 -maximal function
-maximal function 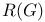
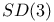 , representations of
, representations of 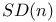
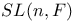
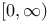
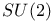 , Haar measure on
, Haar measure on 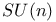
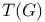 (trigonometric polynomials)
(trigonometric polynomials) 
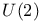 , representations of
, representations of 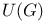
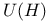
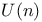 ”)
”) -functions
-functions 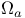
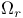

 -algebra of sets
-algebra of sets 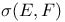 topology
topology 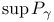
 -mesh
-mesh 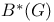
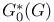
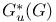
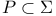
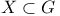


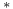 topology
topology 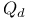
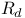
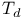
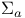
 -topology of
-topology of 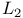
 -measurable implies continuous
-measurable implies continuous