Авторизация
Поиск по указателям
Hewitt E., Ross K.A. — Abstract Harmonic Analysis (Vol. 1)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Abstract Harmonic Analysis (Vol. 1)Авторы: Hewitt E., Ross K.A. Аннотация: Abstract theory remains an indispensable foundation for the study of concrete cases. It shows what the general picture should look like and provides results that are useful again and again. Despite this, however, there are few, if any introductory texts that present a unified picture of the general abstract theory.A Course in Abstract Harmonic Analysis offers a concise, readable introduction to Fourier analysis on groups and unitary representation theory. After a brief review of the relevant parts of Banach algebra theory and spectral theory, the book proceeds to the basic facts about locally compact groups, Haar measure, and unitary representations, including the Gelfand-Raikov existence theorem. The author devotes two chapters to analysis on Abelian groups and compact groups, then explores induced representations, featuring the imprimitivity theorem and its applications. The book concludes with an informal discussion of some further aspects of the representation theory of non-compact, non-Abelian groups.
Язык: Рубрика: Математика /Анализ /Продвинутый анализ /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: Second EditionГод издания: 1979Количество страниц: 519Добавлена в каталог: 02.04.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Lorentz, G. G. 245 Los, J. 425 Lower semicontinuous function 121 Luthar, I. S. 245 Lyubarskii, G.Ya. 261 M(G) 269 M(G) = 273 M(G) is conjugate space of 170 M(G), 272 M(G), 271 M(G), 270 M(G), 273 M(G), 1-dimensional ideals of 309—310 M(G), adjoint operation in 300 M(G), commutative if and only if G is 302 Maak, W. 257 259 261 425 Macbeath, A.M. 229 Mackey, G. W. 229 398 421 425 Mapping 2 Markov, A. A. 32 51 83 104 106 Marriage lemma 248 Matrix (special types defined) 7 Matrix group 7 (see also “Linear group”) Maximal ideal space 478 Mean 230 (see also “Invariant means”) Measurable function 118 125 Measurable representation, weakly 335 Measurable set 125 Measure space, basis of 215 Measure space, character of 215 Measure space, complete 216 Measure space, extension of 216 Measure(s) 118 Measure(s), absolutely continuous 180 269 Measure(s), Caratheodory outer 123 Measure(s), concentrated on a set 180 Measure(s), continuous 269 Measure(s), convolution of 266 Measure(s), Haar 194 (see also “Haar measure”) Measure(s), invariant finitely additive 242—245 Measure(s), inversion invariant 185 Measure(s), left invariant 185 Measure(s), product of 152 Measure(s), product of complex 182 Measure(s), purely discontinuous 269 Measure(s), regular 127 Measure(s), singular 180 269 Measure(s), support of 124 Measure(s), total variation of 169 mesh 13 Metrizability of topological groups 70 Michael, E.A. 83 Michelow, J. 113 Minimal divisible extension of a group 419 445—447 Minkowski’s inequality 138 Modular function 196 Modular function for 438 Modular function on closed normal subgroups 206 Monothetic group 85 390 407—409 Monothetic group, generators of 105 407 415 Monothetic group, largest 407 Monothetic semigroups 105 Montgomery, D. 32 51 66 76 83 106 Multiplicative function 345 Multiplicative linear functional 474 Multiplicity of family of sets 15 Munn, W. D. 282 Mycielski, J. 66 n-dimensional space, compact Hausdorff 15 n-dimensional space, complex and real 3 Nachbin, L. 354 Naimark, M.A. 135 166 334 353 354 Nakayama, T. 83 425 Natural mapping 4 Neighborhood (always open) 9 Net 14 Neumann, J. von 26 32 117 134 214 243 245 283 349 354 425 Nikodym, O.M. 150 Nondiscrete topologies for Abelian groups 27 Nondiscrete topologies for Z 27 Nonmeasurable sets 226 Nonnegative linear functional 461 Nonnegative linear functional on 120 Nonnormal groups 74—76 Norm 453 Norm in 3 Norm in 3 Norm in 135 Norm of linear function 454 Norm topology 454 Norm, uniform 119 230 Normal operator 467 Normal operator, existence of inverse 484 Normal subgroup 16 Normal topological group 16 Normality of locally compact groups 76 Normed 313 Normed algebra 469 Normed linear space 453 Normed linear space, reflexive 457 Normed linear space, weak topology 458 Normed linear space, weak- 458 Nowhere dense 456 Null function 124 Null set 124 Numakura, K. 106 Nussbaum, A. E. 399 Olmsted, J.M.H. 104 One-parameter subgroup 85 Open and closed subgroups 33—34 62 Operators 452 Operators, adjoint 466 Operators, Hermitian 467 Operators, normal 467 Operators, positive-definite 467 Operators, projection 467 Operators, sum of 468 Operators, unitary 467 Ordered groups 24 Orthogonal elements 465 Orthogonal group 7 (see also “ Orthogonal group, special 7 (see also “ Orthogonal matrix 7 Orthogonal set 465 Orthogonal sets 465 Orthonormal basis 465 Orthonormal set 465 Oxtoby, J.C. 215 229 p-adic integers 109 (see also “ p-adic number field 112 (see also “ p-adic numbers 109 (see also “ p-primary group 439 p-rank of a group 444 P-topology 361 Paley, R.E.A.C. 375 Paracompact space 13 Paracompactncss of locally compact groups 76 Partition of a set 2 Partitions of unity 9—10 Pasynkov, B. 398 Peres, J. 282 Permutation group 8 permutations 8 Peter, F. 213 283 311 353 354 375 Pierce, R. S. 413 425 449 Pitt, H.R. 282 Pontryagin — van Kampen duality theorem 378 Pontryagin — van Kampen duality theorem, uniqueness of T 424 Pontryagin, L. S. 32 51 60 80 83 103 106 354 375 397 398 399 424 Positive functional 316 Positive functional, extensible 317 Positive functional, nonextensible 331 Positive linear functional, strictly 461 Positive-definite operator 467 Positive-definite operator, spectrum is nonnegative 484 Positive-definite operator, square root of 484 Preston, G.C. 399 primary group 439 Product of characters 355 Product of complex measures 182 Product of functionals 152 159 Product of groups 6 Product of measures 152 Product of sets 2—3 Product of topological groups 52 Product of topological groups, character group of 362—365 Projection 54 Projection operator 467 Projective limit 56 Proper ideal, of an algebra 469 Proper subgroup 4 Prufer, H. 117 Pure independent set 448 Pure subgroups 447 395 Purely discontinuous measure 269 Quasi-inverse(s) 471 Quasi-inverse(s), form open set 472 Quaternions, Haar measure on 210 Quotient group 4 40 Quotient group, character group of 365 Quotient space 4 452 Quotient space, homogeneity of 37 Quotient space, topology of 36 r-adic integers 109 (see also “ r-adic numbers 109 (see also “ Radon — Nikodym theorem 144 Radon, J. 150 Raikov, D.A. 214 311 334 353 354 375 398 Raimi, R. A. 245 Rank of a group 444 Real algebra 469 Real characters 390 393 Real characters, extensibility of 391 Real linear space 452 Real matrix 7 Real n-dimensional space 3 Real-character group 390 Reduce 323 Reduced group 440 Reduced word 8 Reducible representation 323 Reducible set of operators 323 refinement 13 Reflexive space 457 Regular ideal 475 Regular left ideal 474 Regular measure 127 Regular representation 342 Regular topological space 9 Relatively bounded linear functional 461 Relatively invariant functionals 203 Relatively invariant functionals, examples 212 Representation space 313 Representation(s) of a group 312 Representation(s) of a semigroup 312 Representation(s) of an algebra 312 Representation(s) of an algebra with unit 313 Representation(s), continuous 341 Representation(s), cyclic 315 Representation(s), equivalent 314 Representation(s), invariant subspace under 313 Representation(s), irreducible 323 Representation(s), reducible 323 Representation(s), regular 342 Representation(s), strongly continuous 335 Representation(s), sufficiently many 343 Representation(s), weakly continuous 335 Representation(s), weakly measurable 335 Ricabarra, R. 375 Richardson, R.W. 94 Rickart, C. E. 334 Riesz, F. 134 150 Right Haar integral 195 (see also “Left Haar integral”) Right Haar measure 195 (see also “Left Haar measure”) Right unit relative to I 474—475 (see also “Left unit relative to I”) Ring of sets 118 Riss, J. 398 Robertson, W. 372 Robison, G.B. 237 Rosen, W. G. 215 Rudin, W. 184 425 Ryll-Nardzewski, C. 393 398 Saks, S. 166 Samelson, H. 415 425 Scalar field 452 SCHONEBORN, H. 399 Schreier, O. 31 64 67 Schur, I. 213 Schur’s lemma 324 Schwartz, J.T. 149 166 Schwarz, S. 215 354 Schwarz’s inequality 464 Second category 456 Second character group 376 Second isomorphism theorem for groups 5 Second isomorphism theorem for topological groups 45 Sections 153 Segal, I.E. 3H 334 353 354 Self-dual groups 422 Semicharacter 345 Semicontinuous functions 121 Semidirect product of groups 6—7 Semidirect product of topological groups 58—59 Semidirect product, Haar measure on 210 Semigroup 4 Semigroup, cancellation 258 Semigroup, topological 98 233 Separate points 151 Shiga, K. 353 Signum (sgn) 3 Silverman, R. J. 245 Simple algebra 469 Simple semigroup 100—101 Singular measure 180 269 Skew-Hermitian matrix 7 Skew-symmetric matrix 7 Smith, M.F. 370 399 Solenoidal groups 85 409—410 Solenoidal groups, a-adic 114 Solenoidal groups, largest 410 Special linear group 7 (see also “ Special orthogonal group 7 (see also “ Special unitary group 7 (see also “ Spectral theorem 488—491 Spectral theorem for Hermitian operators 491 Spectral theorem, applied 325 Spectrum 476 Spectrum is compact nonvoid 477 Square root of positive-definite operator 484 Sreider, Yu. A. 311 Steinhaus, H. 150 Stone — Weierstrass theorem 151 281—282 Stone, A.H. 83 Strictly positive linear functional 461 Stromberg, K. R. 397 Stronger topology 9 Strongly continuous representation 335 Struble, R. A. 261 Structure space 477—478 Structure theorem for locally compact, compactly generated Abelian groups 90
Реклама
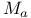is closed ideal 
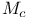is closed ideal 
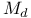is closed subalgebra 
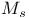is closed linear subspace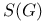 
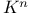
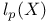
-algebra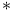 
topology 
”)
”)
”)
”)
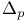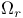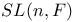F)$"/>”)
”)
”)
|
|
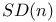О проекте