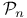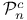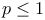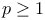|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Borwein P, Erdelyi T — Polynomials and polynomial inequalities |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
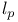 norm 6 48 471 norm 6 48 471
Abel, Niels Henrik 3 61
Algorithms 356—371
Algorithms for Chebyshev polynomials 371
Algorithms for counting zeros 364—370
Algorithms for polynomial evaluations 363
Algorithms for reversion of power series 362
Algorithms, evaluation of 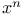 363 363
Algorithms, fast Fourier transform 359
Algorithms, fast polynomial division 362
Algorithms, fast polynomial expansion 363
Algorithms, fast polynomial multiplication 361
Algorithms, interpolation 360
Algorithms, Newton’s method 362 364—367
Algorithms, Remez 371
Algorithms, zero finding for polynomials 366—370
Alternation set 93
Alternation theorem 94
Apolar polynomials 23 24 25
Arc length of algebraic polynomials 31
Arc length of trigonometric polynomials 35
Berman’s formula 166
Bernstein factor 145 150 152 322—328
Bernstein polynomials 163—164
Bernstein — Szego inequality 231 245 259 321—323
Bernstein — Szego inequality for entire functions of exponential type 245
Bernstein — Szego inequality for rational functions on  323 323
Bernstein — Szego inequality for rational functions on K 322
Bernstein — Szego inequality for rational functions on [—1,1] 322
Bernstein — Szego inequality for trigonometric polynomials 232
Bernstein-type inequality for Chebyshev spaces 206
Bernstein-type inequality for constrained polynomials 420—447
Bernstein-type inequality for entire functions of exponential type 245
Bernstein-type inequality for exponential sums 289
Bernstein-type inequality for generalized polynomials 392—416
Bernstein-type inequality for generalized polynomials in  401—417 401—417
Bernstein-type inequality for higher derivatives 258
Bernstein-type inequality for nondense Miintz spaces 213 310
Bernstein-type inequality for polynomials 232—233 390
Bernstein-type inequality for polynomials in  235 390 401—417 235 390 401—417
Bernstein-type inequality for products of Miintz spaces 317
Bernstein-type inequality for rational functions on  323 329 323 329
Bernstein-type inequality for rational functions on D 324
Bernstein-type inequality for rational functions on K 322 327
Bernstein-type inequality for rational functions on [—1,1] 323 327
Bernstein-type inequality for self-reciprocal polynomials 339
Bernstein-type inequality for trigonometric polynomials 232
Bernstein-type inequality, bounded 178 182 213—214
Bernstein-type inequality, unbounded 154 206—217
Bernstein-type inequality, weighted 257
Bessel’s inequality 46
Best approximation 94
Best approximation to 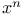 99 99
Best approximation to 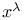 , a problem of Lorentz 108 , a problem of Lorentz 108
Best approximation, uniqueness 98
Best approximationby rationals 99
Binomial coefficient 62
Blaschke product 190 324
Blumenthal’s theorem 78
Bombieri’s norm 274
Bounded Bernstein-type inequality see “Bernstein-type inequality”
Bounded Chebyshev-type inequality see “Chebyshev-type inequality”
Bounded linear functionals 50
Budan — Fourier theorem 369
Cardano, Girolamo 3
Cartan’s lemma 350
Cauchy determinant 106
Cauchy indices 367
Cauchy — Schwarz inequality 42
Cauchy — Schwarz inequality for sequences 46
Cauchy’s integral formula 14
Cesaro means 165
Chebyshev constants 39
Chebyshev polynomials in Chebyshev spaces 114—125
Chebyshev polynomials in rational spaces see “Chebyshev rationals”
Chebyshev polynomials, algorithms for 371
Chebyshev polynomials, best approximation to 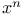 30 30
Chebyshev polynomials, composition, characterization 33
Chebyshev polynomials, explicit formulas 30 32
Chebyshev polynomials, orthogonality 32
Chebyshev polynomials, reducibility 36
Chebyshev polynomials, second kind 37
Chebyshev polynomials, three-term recursion 32
Chebyshev polynomials, trigonometric on subintervals 235
Chebyshev polynomials, uniqueness 118
Chebyshev rationals 139—153
Chebyshev rationals and orthogonality 147
Chebyshev rationals in algebraic rational spaces 142
Chebyshev rationals in trigonometric rational spaces 143
Chebyshev rationals of the first and second kind 141
Chebyshev rationals on the real line 151
Chebyshev rationals, derivative formulas 146
Chebyshev rationals, partial fraction representation 144
Chebyshev space 92
Chebyshev space, dimension on the circle 100
Chebyshev space, functions with prescribed sign changes 100
Chebyshev system 91—100
Chebyshev system, extended complete 97
Chebyshev, P.L. 31
Chebyshev-type inequality for entire functions of exponential type 245
Chebyshev-type inequality, bounded 179 182
Chebyshev-type inequality, explicit bounds via Paley — Weiner theorem 196
Chebyshev’s inequality 235 390
Christoffel function 74
Christoffel function for Miintz spaces 195
Christoffel numbers 67
Christoffel — Darboux formula 60
Coefficient bounds for polynomials in special bases 124
Coefficient bounds in nondense rational spaces 153
Coefficient bounds of Markov 248
Comparison theorem 103 120 122 183
Completeness 48 79
Complexity concerns 356—371
Consecutive zeros of p' 26
Constrained polynomials 417—447
Constrained polynomials,  inequalities 422 inequalities 422
Constrained polynomials, Bernstein-type inequality 420 425 427
Constrained polynomials, Markov-type inequality 417—447
Constrained polynomials, Nikolskii-type 444
Constrained polynomials, Remez-type 443—445
Constrained polynomials, Schur-type 436—437
Cotes numbers 67
Cubic equations 4
de la Vallee Poussin theorem 99
Denseness 154—226
Denseness of Markov spaces 206—217
Denseness of Miintz polynomials 171—205
Denseness of Miintz rationals 218—226
Denseness of polynomials 154—170
Derivatives of Markov systems 112
Descartes system 100—113
Descartes system, examples 103
Descartes system, lexicographic properties 103
Descartes’ Rule of Signs 22 102
Divide and conquer 358
Division of polynomials 15 362
d’Alembert, Jean le Rond 13
Elementary symmetric function 5
Enestrom — Kakeya theorem 12
Erdos inequality 431
Erdos — Turan inequality 435
Euler, Leonhard 13
Evaluation of 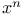 363 363
Exponential sums see “Miintz polynomials”
Exponential sums with nonnegative exponents 294
Exponential sums, a problem of Lorentz 291
Exponential sums, Bernstein-type inequality 291
Exponential sums, Markov-type inequality 294
Exponential sums, Nikolskii-type inequality 289
Exponential sums, Turan’s inequality 295
| Exponential type 196 245
Extended complete Chebyshev system 97
Factor inequalities 260—274
Factor inequalities, via Mahler’s measure 271—273
Factorization 10 36
Fast Fourier Transform 359
Favards theorem 73
Fejer gap 27—28
Fejer operators 164
Fejer’s theorem 165
Fekete point 38
Fekete polynomial 38
Ferrari, Ludovico 3
Ferro, Scipione del 3
Fourier coefficient 53
Fourier series 53
Fundamental theorem of algebra 3
Gamma function 63
Gauss — Jacobi quadrature 67 75
Gauss — Lucas Theorem 18
Gauss, Carl Friedrich 13
Gaussian hypergeometric series 62
Gegenbauer polynomials 65
Generalized polynomials,  inequalities 401—407 inequalities 401—407
Generalized polynomials, Bernstein-type inequality 399 407
Generalized polynomials, Markov-type inequality 399 407
Generalized polynomials, Nikolskii-type inequality 394—395
Generalized polynomials, Remez-type inequality 393—394 414
Generalized polynomials, Schur-type inequality 395
Generalized polynomials, weighted inequalites 407
Girard, Albert 13
Grace’s complex version of Rolle’s theorem 25
Grace’s theorem 18
Gram — Schmidt 44
Gram’s lemma 176
Haar space 92
Haar system 92
Halley’s method 365
Hardy space 189
Helly’s convergence theorem 71
Helly’s selection theorem 71
Hermite interpolation 9
Hermite polynomials 57
Hermite polynomials, explicit formulas 65
Hilbert space 42
Holder’s Inequality 17 49
Horner’s rule 8
Hypergeometric differential equation 63
Hypergeometric functions 62
Identity Theorem 15
Inequalities for Miintz polynomials see “Miintz polynomials”
Inequalities, Bernstein — Szego inequality see “Bernstein — Szego inequality”
Inequalities, Bernstein-type see “Bernstein-type inequality”
Inequalities, Bessel’s see “Bessel’s inequality”
Inequalities, bounded Bernstein-type see “Bounded Bernstein-type inequality”
Inequalities, bounded Chebyshev-type see “Bounded Chebyshev-type inequality”
Inequalities, Cauchy — Schwarz see “Cauchy — Schwarz inequality”
Inequalities, Chebyshev-type see “Chebyshev-type inequality”
Inequalities, for factors see “Factor inequalities”
Inequalities, Holder’s see “Holder’s inequality”
Inequalities, Lax-type see “Lax”
Inequalities, Markov-type see “Markov-type inequality”
Inequalities, metric see “Metric inequalities”
Inequalities, Minkowski’s see “Minkowski’s inequality”
Inequalities, Nikolskii-type see “Nikolskii-type inequality”
Inequalities, Remez-type see “Remez-type inequality”
Inequalities, Russak’s see “Russak”
Inequalities, Schur-type see “Schur-type inequality”
Inequalities, triangle see “Triangle inequality”
Inequalities, unbounded Bernstein-type see “Unbounded Bernstein-type inequality”
Inner product 41
Inner product space 41
Integer-valued polynomials 10
Interpolation, Hermite see “Hermite interpolation”
Interpolation, Lagrange see “Lagrange interpolation”
Interpolation, Newton see “Newton interpolation”
Jacobi polynomials 57 63
Jacobi polynomials, explicit formulas 63
Jensen circles 19
Jensen’s formula 187
Jensen’s Inequality 414
Jensen’s theorem 19
Kernel function 47 132
Kolmogorov’s inequality 285
Korovkin’s theorems 163
Lacunary spaces 308
Lacunary spaces, quasi-Chebyshev polynomials 316
Lagrange interpolation 8
Laguerre polynomials 57 66 130
Laguerre polynomials, explicit formulas 66
Laguerre’s Theorem 20
Lax-type inequality 438
Lax-type inequality for rationals 329
Lax-type inequality on a half-plane 338
Lax-type inequality, Malik’s extension 438
Legendre polynomials 57
Lemniscates of constant modulus 352—353
Lexicographic properties 116
Lexicographic properties for Miintz polynomials 120 314
Lexicographic properties for Muntz — Legendre polynomials 136
Lexicographic properties for sinh systems 122
Liouville’s theorem 15
Logarithmic capacity 38
Lorentz degree 82
Lorentz degree for polynomials 86
Lorentz degree for trigonometric polynomials 89
Lorentz’s problem 108 291
Lucas’ Theorem 18
m-distribution 57
Mahler’s measure 271
Mairhuber theorem 98
Markov system 100
Markov system, closure of nondense 211
Markov system, derivative of 112
Markov — Stieltjes inequality 76
Markov-type inequality for 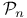 233 233
Markov-type inequality for 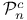 255 255
Markov-type inequality for constrained polynomials 417—447
Markov-type inequality for constrained polynomials in  422 428—429 422 428—429
Markov-type inequality for exponential sums 276—280 294—295
Markov-type inequality for generalized polynomials 399—407 445
Markov-type inequality for generalized polynomials in  401—407 401—407
Markov-type inequality for higher derivatives 248—260
Markov-type inequality for monotone polynomials 439—441
Markov-type inequality for Muntz polynomials 276—279 287—288
Markov-type inequality for Muntz polynomials in  279—280 279—280
Markov-type inequality for nonnegative polynomials 420 439
Markov-type inequality for rational functions 336
Markov-type inequality for self-reciprocal polynomials 339
Markov-type inequality for trigonometric polynomials on subintervals 242—245
Markov-type inequality in the complex plane 235
Markov-type inequality, weighted 442—443
Maximum principal 15
Mergelyan’s theorem 170
Mesh of zeros 155
Metric inequalities 344—355
Metric inequalities for polynomials 345—346
Metric inequalities for rational functions 347—349
Metric inequalities in  , , 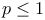 52 52
Minkowski’s inequality in  , , 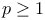 49 49
moment 57
Moment problem 70
Monotone operator theorem 163
Multiplication of polynomials 361
Muntz polynomials, bound for smallest zero 313
Muntz polynomials, bounded Bernstein-type inequality 178 182 213 310 317
Muntz polynomials, lexicographic properties of zeros 116 120
Muntz polynomials, Newman’s inequality 276 301
Muntz polynomials, Newman’s inequality in  279 279
Muntz polynomials, Newman’s problem 317
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



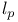 norm
norm 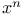


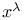 , a problem of Lorentz
, a problem of Lorentz