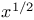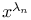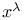|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Borwein P, Erdelyi T — Polynomials and polynomial inequalities |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Muntz polynomials, Nikolskii-type inequality 281 298 317
Muntz polynomials, positive zeros 22
Muntz polynomials, Remez-type inequality 304 307 316
Muntz polynomials, where the sup norm lives 301
Muntz rationals 218—226
Muntz rationals, denseness 218
Muntz space 125—126
Muntz space, lexicographic properties of zeros 120
Muntz space, products of 222 316
Muntz space, quotients of 218—226
Muntz system 125—136
Muntz system, closure 171—205
Muntz system, nondense 303—319
Muntz — Legendre polynomials 125—138
Muntz — Legendre polynomials, definition 126
Muntz — Legendre polynomials, differential recursion 129
Muntz — Legendre polynomials, global estimate of zeros 136
Muntz — Legendre polynomials, integral recursion 132
Muntz — Legendre polynomials, lexicographic properties of zeros 133—136
Muntz — Legendre polynomials, orthogonality 127 132
Muntz — Legendre polynomials, orthonormality 128
Muntz — Legendre polynomials, Rodrigues-type formula 128 131
Muntz — Legendre polynomials, zeros of 133
Muntz’s theorem 171—205
Muntz’s theorem in ![$L_2[0,1]$](/math_tex/9995872b7fae100e1a05b0003beffe9a82.gif) 171 171
Muntz’s theorem in 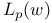 311 311
Muntz’s theorem in ![$L_p[0,l]$](/math_tex/82342a38bfb55fd7a67523e248f2080f82.gif) 172 172
Muntz’s theorem in ![$L_p[a, b]$](/math_tex/68bc2bc72c9fabc3bd8cc413097bfb0082.gif) 186 186
Muntz’s theorem in C[0,1] 171
Muntz’s theorem in C[a, b] 180 184
Muntz’s theorem on sets of positive measure 303
Muntz’s theorem, another proof 176 192
Muntz’s theorem, closure of span in 178 181 185
Newman’s conjecture on denseness of products 316
Newman’s conjecture on denseness of quotients 220 223
Newman’s inequality 275—279
Newman’s inequality for Muntz polynomials 276
Newman’s inequality for Muntz polynomials in  279 279
Newman’s inequality on positive intervals 301
Newman’s inequality, an improvement 287
Newton Interpolation 10
Newton’s identities 5
Newton’s method 362 364—367
Newton’s method for 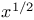 365 365
Newton’s method in many variables 366
Nikolskii-type inequality for constrained polynomials 444
Nikolskii-type inequality for exponential sums 289
Nikolskii-type inequality for generalized polynomials 394 395
Nikolskii-type inequality for Muntz polynomials 281 298 317
Nikolskii-type inequality for products of Muntz spaces 317
Nondense Muntz spaces 303—319
Nonnegative polynomials 70 85 417 420
Nonnegative trigonometric polynomials 85 409
Norms 471
Norms,  see “ see “ norm” norm”
Norms, supremum see “Supremum norm”
Orthogonal collection 43
Orthogonal functions 41—56
Orthogonal polynomials 57—79
Orthogonal polynomials as continued fractions 79
Orthogonal polynomials as determinants 76
Orthogonal polynomials, characterization of compact support 77
Orthogonal polynomials, Gegenbauer see “Gegenbauer polynomials”
Orthogonal polynomials, Hermite see “Hermite polynomials”
Orthogonal polynomials, interlacing of zeros 61
Orthogonal polynomials, Jacobi see “Jacobi polynomials”
Orthogonal polynomials, Laguerre see “Laguerre polynomials”
Orthogonal polynomials, Legendre see “Legendre polynomials”
Orthogonal polynomials, Muntz — Legendre see “Muntz — Legendre polynomials”
Orthogonal polynomials, simple real zeros 61
Orthogonal polynomials, ultraspherical see “Ultraspherical polynomials”
Orthogonal rational functions 147
Orthonormal set 43
Paley — Weiner theorem 196
Parallelogram law 42
Parseval’s identity 48
Partial fraction decomposition 7 144
Pellet’s theorem 16
Polar derivative 20
Polynomials as sums of squares 85 348
Polynomials in 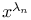 167 167
Polynomials with integer coefficients 169
Polynomials with nonnegative coefficients 79—90 417
Polynomials with real roots 345 347—348
Polynomials, Bernstein see “Bernstein polynomials”
Polynomials, Chebyshev see “Chebyshev polynomials”
Polynomials, Gegenbauer see “Gegenbauer polynomials”
Polynomials, generalized see “Generalized polynomials”
Polynomials, growth in the complex plane 239
Polynomials, Hermite see “Hermite polynomials”
Polynomials, integer valued see “Integer valued polynomials”
Polynomials, Jacobi see “Jacobi polynomials”
Polynomials, Laguerre see “Laguerre polynomials”
Polynomials, Legendre see “Legendre polynomials”
Polynomials, Muntz see “Muntz polynomial”
Polynomials, Muntz — Legendre see “Muntz — Legendre polynomials”
Polynomials, number of real roots 17 137
Polynomials, symmetric 5
Polynomials, trigonometric see “Trigonometric polynomial”
Polynomials, ultraspherical see “Ultraspherical polynomials”
Products of Muntz spaces 222 316
Quadratic equations 4
| Quartic equations 4
Quasi-Chebyshev polynomials 316 342
Railway track theorem 98
Rakhmanov’s theorem 78
Rational functions, algebraic 139
Rational functions, Chebyshev polynomials of 139—153
Rational functions, coefficient bounds 153
Rational functions, inequalities see “Inequalities”
Rational functions, trigonometric 139
Rational spaces of algebraic rational functions 139—153 320—321
Rational spaces of trigonometric rational functions 139—153 320—321
Recursive bounds 359
Remez-type inequality for algebraic polynomials 228
Remez-type inequality for constrained polynomials 443 445
Remez-type inequality for generalized polynomials 393 394
Remez-type inequality for generalized polynomials in  401—402 401—402
Remez-type inequality for Muntz spaces 307
Remez-type inequality for nondense Muntz spaces 304
Remez-type inequality for products of Muntz spaces 316
Remez-type inequality for trigonometric polynomials 230
Remez-type inequality, pointwise 414
Remez’s algorithm 371
Reproducing kernel 47 132
Reversion of power series 362
Riemann — Lebesgue lemma 54
Riesz representation theorem 50
Riesz — Fischer theorem 50
Riesz’s identity 390
Riesz’s lemma 237
Rising factorial 62
Rolle’s Theorem 25
Rouche’s Theorem 14 16
Russak’s inequalities 336
Salem numbers 6
Schur-type inequality for algebraic polynomials 233
Schur-type inequality for constrained polynomials 436—437
Schur-type inequality for generalized polynomials 395
Schur-type inequality for rational functions 337
Schur-type inequality for trigonometric polynomials 238
Schur’s Theorem 17
Self-reciprocal polynomials 339
Self-reciprocal polynomials, quasi-Chebyshev polynomials 342
Somorjai’s theorem 218
Space, Chebyshev see “Chebyshev space”
Space, Descartes see “Descartes space”
Space, Haar see “Haar space”
Space, Muntz see “Muntz space”
Space, rational see “Rational space”
Stieltjes’ theorem 78
Stone — Weierstrass theorem 161
Sums of squares of polynomials 85 348
Supremum norm 6 29 471
Symmetric function 5
Symmetric polynomial 5
Szego’s inequality 391
Szego’s theorem 23 235
Tartaglia, Niccolo 3
Tchebychev see “Chebyshev”
Three-term recursion 59
Totally positive kernels 110
Transfinite diameter 38
Triangle inequality 42
Trigonometric polynomial 2
Trigonometric polynomials of longest arc length 35
Turan’s inequality 434
Turan’s inequality for exponential sums 295
Ultraspherical polynomials 65
Unbounded Bernstein-type inequality 206—217
Unbounded Bernstein-type inequality, characterization of denseness 207
Unicity theorem 15
Vandermonde determinant 38 103
Variation diminishing property 111
Videnskii’s inequalities 242—245
Walsh’s two circle theorem 20
Weierstrass’ theorem 154—170
Weierstrass’ theorem for Markov systems 155
Weierstrass’ theorem for polynomials 159
Weierstrass’ theorem for polynomials in 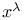 167 167
Weierstrass’ theorem for polynomials with integer coefficients 169
Weierstrass’ theorem for trigonometric polynomials 165
Weierstrass’ theorem in  169 169
Weierstrass’ theorem on arcs 170
Weierstrass’ theorem, Stone — Weierstrass theorem 161
wronskian 22
zeros 11—18
Zeros in a disk 369
Zeros in an interval 368
Zeros in Chebyshev spaces 99
Zeros of Chebyshev polynomials 34 116 120 122
Zeros of derivatives of polynomials 18—28
Zeros of integrals of polynomials 24
Zeros of Muntz polynomials 120
Zeros of Muntz-Legendre polynomials 133—136
Zeros of orthogonal polynomials 61
Zeros, algorithms for finding 364—367
Zeros, complexity of 367
Zeros, counting by winding number 370
Zeros, localizing 367
Zeros, maximum number at one 137
Zeros, maximum number of positive 17
Zolotarev 35
Zoomers 218
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



![$L_2[0,1]$](/math_tex/9995872b7fae100e1a05b0003beffe9a82.gif)
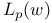
![$L_p[0,l]$](/math_tex/82342a38bfb55fd7a67523e248f2080f82.gif)
![$L_p[a, b]$](/math_tex/68bc2bc72c9fabc3bd8cc413097bfb0082.gif)