|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rickart C.E. — General Theory of Banach Algebras |
|
|
 |
| Предметный указатель |
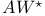 -algebras 84 289—290 -algebras 84 289—290
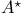 -algebras 181 -algebras 181
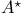 -algebras, continuity of homomorphisms into (4.1.20) 188 -algebras, continuity of homomorphisms into (4.1.20) 188
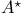 -algebras, non-symmetric A -algebras, non-symmetric A -algebra 324 -algebra 324
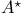 -algebras, representation on Hilbert space (4.8.12) 244 -algebras, representation on Hilbert space (4.8.12) 244
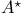 -algebras, uniqueness of norm 188 -algebras, uniqueness of norm 188
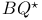 -algebras 194 -algebras 194
 -algebras 3 180 ( 4.9) 239—260 -algebras 3 180 ( 4.9) 239—260
 -algebras, adjunction of an identity (4.1.13) 186 -algebras, adjunction of an identity (4.1.13) 186
 -algebras, annihilator -algebras, annihilator  -algebras (4.10.14) 267 (4.10.20) -algebras (4.10.14) 267 (4.10.20)
 -algebras, approximate identity (4.8.14) 245 -algebras, approximate identity (4.8.14) 245
 -algebras, closed 2-sided ideals are -algebras, closed 2-sided ideals are  -ideals (4.9.2) 249 -ideals (4.9.2) 249
 -algebras, dual -algebras, dual  -algebras (4.10.25) 271 -algebras (4.10.25) 271
 -algebras, isometric isomorphisms are -algebras, isometric isomorphisms are  -isomorphisms (4.8.19)248 -isomorphisms (4.8.19)248
 -algebras, operational calculus (4.8.7) 241 -algebras, operational calculus (4.8.7) 241
 -algebras, representation as -algebras, representation as 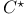 -algebras (4.8.11)244 -algebras (4.8.11)244
 -algebras, structure of ideals (4.9.6) 251 (4.9.8) (4.9.9) (4.9.13) -algebras, structure of ideals (4.9.6) 251 (4.9.8) (4.9.9) (4.9.13)
 -algebras, structure space properties 256—259 -algebras, structure space properties 256—259
 -algebras, symmetry (4.8.9) 243 -algebras, symmetry (4.8.9) 243
 -algebras, topological implies strict irreducibility (4.9.10)253 -algebras, topological implies strict irreducibility (4.9.10)253
 -algebras, uniqueness of the involution (4.8.18) 247 -algebras, uniqueness of the involution (4.8.18) 247
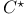 -algebra 181 -algebra 181
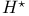 -algebras 272—276 287 -algebras 272—276 287
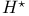 -algebras, right -algebras, right 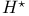 -algebras 276 -algebras 276
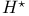 -algebras, Wedderburn structure theorems (4.10.29) 273 (4.10.31) (4.10.32) -algebras, Wedderburn structure theorems (4.10.29) 273 (4.10.31) (4.10.32)
 -algebras (A.2.2) 296—298 -algebras (A.2.2) 296—298
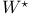 -algebras ( -algebras (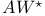 -algebras) 84 96 289—290 -algebras) 84 96 289—290
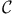 -boundary 132 -boundary 132
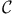 -set (minimal) 132 -set (minimal) 132
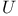 -boundary 142 -boundary 142
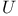 -topology 110 -topology 110
 -algebras 178 (see also “Star algebras” “Algebras -algebras 178 (see also “Star algebras” “Algebras
 -algebras with minimal ideals ( -algebras with minimal ideals (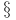 4.10) 260—276 4.10) 260—276
 -homomorphism 180 -homomorphism 180
 -ideal 179 -ideal 179
 -isomorphism 180 -isomorphism 180
 -normed algebra 180 -normed algebra 180
 -radical 210 225—230 (4.7.15) -radical 210 225—230 (4.7.15)
 -radical, Kelley — Vaught characterization (4.6.11)228 -radical, Kelley — Vaught characterization (4.6.11)228
 -representations (4.3.3) 196 -representations (4.3.3) 196
 -representations, associated with hermitian functional (4.3.7) 201 -representations, associated with hermitian functional (4.3.7) 201
 -representations, associated with positive functional ( -representations, associated with positive functional (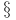 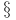 4.5 4.6) 4.5 4.6)
 -representations, cyclic 205 -representations, cyclic 205
 -representations, direct sum of (4.3.4) 198 -representations, direct sum of (4.3.4) 198
 -representations, essential 205 (4.10.24) -representations, essential 205 (4.10.24)
 -representations, extension of (4.7.20) 237 -representations, extension of (4.7.20) 237
 -representations, irreducible 205 (4.4.9) ( (4.10.24) -representations, irreducible 205 (4.4.9) ( (4.10.24)
 -representations, of a -representations, of a  -normed algebra on a self-dual space (4.3.9) 202 -normed algebra on a self-dual space (4.3.9) 202
 -representations, on Hilbert space ( -representations, on Hilbert space (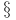 4.4) 205—212 217 4.4) 205—212 217
 -representations, unitary equivalence 205 -representations, unitary equivalence 205
 -semi-simplicity (4.4.9) 210 322 -semi-simplicity (4.4.9) 210 322
 -semi-simplicity, implies -semi-simplicity, implies 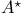 -algebra (4.6.10) 226 -algebra (4.6.10) 226
 -subalgebras 178 -subalgebras 178
 -subalgebras, which contain (quasi-) inverses (4.1.9) 185 -subalgebras, which contain (quasi-) inverses (4.1.9) 185
Absolute value of hermitian elements 243
Absolutely convergent Fourier series (A.2.3) 298—300
Adjoint in an 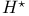 -algebra 272 -algebra 272
Adjoint of an operator on a self-dual space 196
Adjoint of an operator w.r.t. a bilinear form 63
Adjunction of an identity 3 4
Adjunction of an identity, to a  -algebra (4.1.13) 186 -algebra (4.1.13) 186
Admissible positive functional 213
Adverse (= quasi-inverse) 19
Algebra of operators (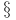 A.l) 277—292 (A.3.6) A.l) 277—292 (A.3.6)
Algebra of power series (A.2.12) 317—318
Algebra of sequences 26
Algebra of set functions (A.2.10) 312—316
Algebra with involution (=  -algebra) 178 -algebra) 178
Algebra with minimal ideals 67—70 ( 96—107 (
Algebra without an involution 306
Algebra, generated by a set of elements 112
Algebraic polyhedron 151
Almost invariant functions 330
Almost periodic functions (A.3.5) 331
Annihilator algebras (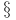 2.8) 96—107 2.8) 96—107
Annihilator algebras,  -algebras 266 287 289 -algebras 266 287 289
Annihilator algebras, B -algebras (4.10.20) 269 -algebras (4.10.20) 269
Annihilator algebras, necessary and sufficient condition (2.8.23) 104
Annihilator ideals 96
Anti-symmetric algebras 304
Approximate identity 3
Approximate identity in 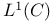 321 321
Approximate identity in a B -algebra (4.8.14) 245 -algebra (4.8.14) 245
Auxiliary norm 181 186
Baer rings 290
Banach algebra 2
Banach algebra of power series 317
Banach — Stone Theorem 248
Belong to A (near a point, at  , locally) 88—90 , locally) 88—90
Bilinear form 62
Bilinear form, non-degeneracy 62
Bilinear form, scalar product 195
Bohr compactification 331
Bound of a bilinear form (2.4.8) 62
Bound of a scalar product (4.3.1) 194
Boundary-value algebra 304
Bounded complete lattice of continuous functions 294
Canonical mapping and representation of the carrier space 113
Carrier space (3.1.3) 110
Carrier space, approximation by finitely generated algebras (3.4.6) 153
Carrier space, canonical representation of 113
Carrier space, homeomorphism induced by an involution 189
Carrier space, of an algebra with one generator (3.4.5) 152
Carrier space, of an algebra with several generators 153 308
Carrier space, of subdirect sums 128—131
Carrier space, of the complexiflcation (3.1.4) 111
Carrier space, representations of (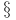 3.4) 149—156 3.4) 149—156
Carrier space, topology determined by system of generators 112
Cauchy integral formula 158
Cauchy integral formula, Herve generalization 160
Cauchy integral formula, Weil generalization 159
Cauchy — Schwartz inequality 195 213
CCR-algebras 284
Center of a normed algebra 35 61 71 85 86
Central and weakly central algebras (2.7.6) 86
centralizer 211
Characterizations of 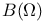 295 295
Characterizations of 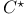 -algebras (4.8.11) 244 -algebras (4.8.11) 244
Characterizations of 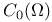 (4.2.2) 190 (4.2.2) 190
Characterizations of  280 280
Characters of a group 325 330
Characters of a group, generalized 330
Circle operation 16
Commutative  -algebras ( -algebras ( 4.2) 189—194 4.2) 189—194
Commutative subset of an algebra 34 (1.6.14)
Commutativity modulo the radical 120
Compact groups 320 330
Compact operators (4.10.17) 268 (4.10.20) (A.1.2)
Completely continuous (algebra) 284
Completely continuous (algebra), operators (= compact operators) 283
Completely regular algebras ( 2.7) 83—96 ( (A.2.3—A.2.5) 2.7) 83—96 ( (A.2.3—A.2.5)
Complex algebras 2
Complexification of a real normed algebra ( 1.3) 5—9 1.3) 5—9
Composition series 284
Cone 227
Continuity of the spectrum (1.6.17) 36 282
Continuous at zero (2.7.31)95
Continuous homomorphisms (2.5.16) 74 (2.5.17) (4.1.20)
Continuous involution 180 (4.1.15)
Continuous subdirect sum 177
Continuously generated subalgebra 165—167 (3.7.4)
Convex set of positive functionals (4.6.2) 222
Convolution algebras (A.2.10—A.2.11) 312—316 (A.3.1-A.3.9)
Cross norm 287
Cyclic subalgebra (strictly, topologically) 47
Cyclic subspace w.r.t. a representation 206
Cyclic vector (strictly, topologically) 47
Decomposable algebra 167—169
Difference space (algebra) 44 144
Direct sum, decomposition 167
| Direct sum, normed full direct sum 77 256
Direct sum, of  -algebras 271—272 -algebras 271—272
Direct sum, of  -representations (4.3.4) 198 (4.4.7) (4.4.8) (4.10.25) 284 “Subdirect -representations (4.3.4) 198 (4.4.7) (4.4.8) (4.10.25) 284 “Subdirect
Direct sum, of cyclic representations (4.4.8) 209
Direct sum, of ideals 46 (2.8.15) (4.10.12) (4.10.14) (4.10.31)
Direct topological sum of ideals 46
Disc algebra 23 303
Division algebras 38—40
Divisors of zero see “Topological divisors of zero”
Dual algebras (2.8.1) 76 (2.8.27 2.8.28) (2.8.29) (4.10.20)269 (4.10.25) (4.10.26) 330
Dual mapping 116 175
Dual vector spaces 62—67
Ecto-ideal 318
Endo-ideal 318
Equivalence of holomorphic functions on  157 157
Equivalence of normed self-dual vector spaces 195
Equivalence of representations (algebraic, topological) 47
Equivalence, unitary equivalence 205—209
Essential  -representation 205 (4.4.8) -representation 205 (4.4.8)
Existence of an identity in a commutative Banach algebra (3.6.6) 169
Exponential function 13
Extreme points 223 225 229 235 251 254
Extremely disconnected space 294
Finitely generated algebras 153
Frobenius’ theorem 40
Full subalgebra generated by a set of elements 291
Functionals see “Hermitian functional” “Positive
Functions of bounded variation (A.2.5) 302—303
Functions of class 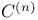 (A.2.4) 300—302 (A.2.4) 300—302
Functions, belong to 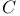 on a set (3.2.19) 127 on a set (3.2.19) 127
Functions, belong to A (near a point, at oo, locally) (2.7.13) 88
Functions, which operate on 51 167
Fundamental isomorphism theorem (2.5.19) 76
Fundamental isomorphism theorem for  -algebras 263 (4.10.9) -algebras 263 (4.10.9)
GCR-algebras 284
Gelfand representation theorem (3.1.20) 119
Gelfand — Naimark Theorems (4.2.2) 190 (4.8.11)244
Generalized analytic functions 148
Generalized divisors of zero 27
Generators of an Algebra (subalgebra) 112
Germ of a holomorphic function 157
Group algebras (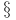 A.3) 318—332 A.3) 318—332
Group algebras, commutative (A.3.2) 325—328
Group algebras, compact groups (A.3.4) 330—331
Group algebras, involution in 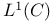 322 322
Group algebras, non-symmetric group algebras 324—325
Group algebras, of operators (A.3.6) 331—332
Group algebras, semi-simplicity of 323
Group of regular (quasi-regular) elements (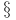 1.4) 9—19 1.4) 9—19
Group of regular (quasi-regular) elements, boundary consists of topological divisors of zero (1.5.4) 22
Group of regular (quasi-regular) elements, number of components (1.4.14) 15 294 314
Group of regular (quasi-regular) elements, principal component (1.4.9) 13 (1.4.10) 19
Haar measure 319
Hausdorff structure space 82 83
Hermitian components of elements in a  -algebra 179 -algebra 179
Hermitian components of functionals on a  -algebra (4.3.6) 200 -algebra (4.3.6) 200
Hermitian elements 178
Hermitian elements, absolute value of 243
Hermitian elements, partial ordering of 231
Hermitian elements, positive and negative parts of 243
Hermitian functional 198
Hermitian functional, associated  -representation (4.3.7) 201 -representation (4.3.7) 201
Hermitian functional, included in another 220
Hermitian functional, not a linear combination of positive functionals 305
Hermitian involution (4.1.6) 184
Holomorphic functions (A.2.6 A.2.7)
Holomorphic on  157 157
Holomorphically generated subalgebra 164
Holomorphically generated subalgebra,  -holomorphically generated subalgebra 165 -holomorphically generated subalgebra 165
Homomorphisms,  -homomorphism 180 -homomorphism 180
Homomorphisms, extensions of (3.3.26) 147 156 163
Homomorphisms, into the complex field 109
Homomorphisms, natural homomorphism 44
Homomorphisms, of function algebras into Banach algebras (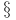 3.5) 156—167 3.5) 156—167
Hull (2.6.2) 78 81 (3.1.14) 116
Hull, compact hulls (2.6.4 2.6.5) (2.7.10) (3.6.7) (3.6.14)
Hull-kernel topology 78
Hull-kernel topology, not equivalent to 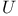 -topology 115 304 -topology 115 304
Hull-kernel topology, of the carrier space 115
Hull-kernel topology, of the structure spaces 78 82
Ideals (left, right 2-sided proper) 41
Ideals, contained in modular ideals (2.7.25) 91 (4.2.6) 327
Ideals, dense in the algebra (4.2.6) 194
Ideals, in 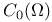 (4.2.4) 193 (4.2.4) 193
Ideals, intersections of maximal modular ideals 327
Ideals, intersections of primary ideals 302
Idempotents 35 71 118 261 294 295
Idempotents, given by a decomposition of carrier space (3.6.3) 168
Idempotents, minimal (2.1.7) 45 261
Idempotents, modulo the radical (2.3.9) 58
Idempotents, orthogonal (maximal family) (2.1.7) 45 266
Idempotents, SBI-rings 58
Integral operators 285
Invariant, almost invariant functions 330
Invariant, family of functions on a group 319
Invariant, functional (integral) 319 (see also “Representations” “
Inverse (left, right) 9
Inverse (left, right), continuity of (1.4.8) 13
Inverse (left, right), relative inverse 96
Inverse (left, right), series representation of (1.4.4) 12 (see also “Quasi-inverse”)
Involution 178
Involution,  -condition 180 -condition 180
Involution, an algebra with no involution 306
Involution, continuity (local) 180 (4.1.5)
Involution, hermitian (4.1.6) 184
Involution, in a symmetric algebra (4.1.5) 233
Involution, in an algebra of operators 264
Involution, uniqueness in a  -algebra (4.8.18) 247 296 -algebra (4.8.18) 247 296
Irreducibility of representations 48 (4.4.9) 221—224
Irreducibility, equivalent to 1-fold transitivity 60
Irreducibility, strictly irreducible 48
Irreducibility, strpngly irreducible 264
Irreducibility, topologically irreducible 48 205 (4.4.12)211
Isomorphism of group algebras 322
Joint spectrum 150
Kadison theorem (4.9.10) 253
Kelley — Vaught characterization of  -radical (4.6.11)228 -radical (4.6.11)228
Krein extension theorem 227
Krein — Millman theorem 225 229 252
Left (right) primitive ideals 179
Linear functional see “Hermitian functionals” “Positive
Liouville theorem 40
Local continuity 180
Local identities 170
Logarithm of elements in a Banach algebra 14
Matrix algebra (full) 275
Matrix algebra (full), representation of simple 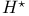 -algebra (4.10.32) 275 -algebra (4.10.32) 275
Matrix Units (complete system) (4.10.21) 269 270
Maximal (-closed, modular) ideals 42—43 (2.8.5) (2.8.7) (3.1.2)
Maximal ideal space 82 120
Maximal subalgebras 305 306
Maximal subalgebras, commutative (1.6.14) 35
Maximal subalgebras, normal (4.1.3) 182
Maximizing set 132
Maximum Modulus Principle 132
Maximum modulus principle, local 148
Maximum point (unique) 141 (3.3.17)
Maximum set for a function (special) 138
Mazur — Gelfand theorem 1 (1.7.1) 40
Meso-ideal 318
Metric ring 3
Minimal 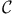 -set (special) 132 139 -set (special) 132 139
Minimal (-closed) ideals 41 43 46 98 99 262 267
Minimal boundary 142
Modular ideals 42 47
Multiplicative condition 2
N-algebra (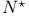 -algebra) 92—93 (2.7.30) 300—303 326 -algebra) 92—93 (2.7.30) 300—303 326
Natural embedding 120—123
Natural homomorphism 44
Nil ideal see “Topologically nil ideal”
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -algebras
-algebras 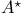 -algebras
-algebras  -algebra
-algebra 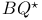 -algebras
-algebras  -algebras
-algebras 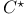 -algebras
-algebras 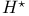 -algebras
-algebras  -algebras
-algebras 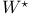 -algebras (
-algebras (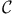 -boundary
-boundary 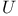 -boundary
-boundary 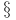 4.10) 260—276
4.10) 260—276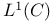
 , locally)
, locally) 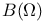
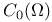
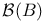

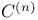
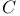 on a set
on a set  -holomorphically generated subalgebra
-holomorphically generated subalgebra 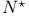 -algebra)
-algebra)