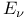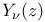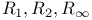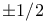|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Олвер Ф. — Введение в асимптотику и специальные функции |
|
|
 |
| Предметный указатель |
Абель 14
Абеля теорема о непрерывности степенного ряда 42
Абеля тождество 182
Айнс 240 296
Ангора функция 112 135
Асимптотика 43
Асимптотическая переменная 29
Асимптотическая последовательность 40
Асимптотическая сумма 38
Асимптотическая шкала 40
Асимптотические приближения см. «Асимптотическое разложение асимптотические
Асимптотические решения дифференциальных уравнений см. «Дифференциальные уравнения»
Асимптотические соотношения 15—19 40
Асимптотическое поведение степенного ряда на границе круга сходимости 42
Асимптотическое разложение 15 12 «Асимптотика» «Дифференциальные
Асимптотическое разложение интегралов 90—95 100—100 139—146 «Лапласа «Метод «Метод
Асимптотическое разложение обобщенное 41 46 153
Асимптотическое разложение составное 153
Асимптотическое разложение, граничная постоянная 16 18 29
Асимптотическое разложение, до N-го члена 30
Асимптотическое разложение, единственность 30
Асимптотическое разложение, история 14 46
Асимптотическое разложение, операции 33—37
Асимптотическое разложение, определение Пуанкаре 14 29 40 137
Асимптотическое разложение, основные свойства 29—32
Асимптотическое разложение, сходимость 31 32
Асимптотическое разложение, функции с заданными асимптотическими разложениями 37—39 46
Асимптотическое разложение, экспоненциально малые члены 104——105 126 137
Асимптотическое решение дифференциальных уравнений см. «Дифференциальные уравнения»
Б. А. (British Association for the Advancement of Science) 173
Барнс 84
Бахман 15
Берг 46
Бесселя уравнение 79
Бесселя уравнение модифицированное 83
Бесселя уравнение неоднородное 352
Бесселя уравнение, численно удовлетворительные решения 309—310 356
Бесселя функции 78 80 310 «Ганкеля «Модифицированные
Бесселя функции мнимого аргумента 83
Бесселя функции первого, второго, третьего рода 309
Бесселя функции полуцелого порядка 82 309 312
Бесселя функции при больших значениях аргумента 169 310 345
Бесселя функции производные по порядку 311 313
Бесселя функции, аналитическое продолжение 80 314
Бесселя функции, вронскиан 312
Бесселя функции, графики 311
Бесселя функции, дифференциальное уравнение 79
Бесселя функции, интеграл Бесселя 78
Бесселя функции, интеграл Пуассона 83
Бесселя функции, интегралы 82 83 313 356 357
Бесселя функции, интегралы Мелера — Сонина 312
Бесселя функции, интегралы Шлефли 81
Бесселя функции, интегральные представления 78—82 312 355 356
Бесселя функции, история 356
Бесселя функции, нули 273 313—320 356
Бесселя функции, оценки 82
Бесселя функции, производящая функция 79
Бесселя функции, рекуррентные формулы 81
Бесселя функции, ряды 78 80
Бесселя функции, связь с вырожденной гипергеометрической функцией 327
Бесселя функции, теорема сложения Неймана 82
Бесселя функции, формулы связи 305 306 309—312
Бета-функция 53 54
Блайстейн 137 138
Бриллюэн 291
Бромуич 12 34 46
Буркхардт 137
Бухгольц 356
Бэкхум 112
Вазов 356
Ван-дер-Корпут 43
Вариационный оператор 43
Вариация 43—45
Вариация, сходимость в особой точке 256—258
Ватсон 46 88 96 137 195 206 240 291 315 319 325 344 345 356
Ватсона лемма для действительных переменных 95
Ватсона лемма для интегралов по петле 156
Ватсона лемма для комплексных переменных 146
Ватсона лемма, история 137
Ватсона лемма, оценки остатка 118—122 137 149—151
Вебер 135
Вебера дифференциальное уравнение 188 264 273
Вебера функции параболического цилиндра см. «Функции параболического цилиндра»
Вебера функция 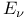 135 135
Вебера функция 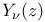 245 (см. также «Функции Бесселя») 245 (см. также «Функции Бесселя»)
Вентцель 291
Вероятностей интеграл 62 89
Вероятностей интеграл дополнительный 62
Вероятностей интеграл, асимптотическое разложение 91 146
Вероятностей интеграл, связь с гамма-функцией 65
Весовая функция 65
ВКБ-метод 291—292
Войн 138
Вполне монотонная функция 93 95
Вронскиан 181
Выделенная точка 17 40
Вырожденная гипергеометрическая функция 326 (см. также «Лагерра полиномы» «Уиттекера
Вырожденная гипергеометрическая функция при больших значениях аргумента 328—330
Вырожденная гипергеометрическая функция, вронскиан 327 331
Вырожденная гипергеометрическая функция, зависимость от параметров 326
Вырожденная гипергеометрическая функция, интегральные представления 327—329
Вырожденная гипергеометрическая функция, история 356
Вырожденная гипергеометрическая функция, преобразования Куммера 328 329
Вырожденная гипергеометрическая функция, рекуррентные формулы 328 332
Вырожденное гипергеометрическое уравнение 325 (см. также «Уиттекера уравнение»)
Вырожденное гипергеометрическое уравнение с показателями, отличающимися на целое число 331
Вырожденное гипергеометрическое уравнение, асимптотические решения 328
Вырожденное гипергеометрическое уравнение, формулы связи для решений 329—332
Вырожденное гипергеометрическое уравнение, численно удовлетворительные решения 332
Гамма-функция 47 (см. также «Гамма-функция неполная» «Пси-функция»)
Гамма-функция неполная 64 89 131
Гамма-функция неполная, асимптотическое разложение 90—91 94—95 143—146 174
Гамма-функция неполная, дополнительная 64 65
Гамма-функция неполная, оценки 91 95 174
Гамма-функция неполная, связь с гипергеометрической функцией 95
Гамма-функция, асимптотическое разложение 113—117 143
Гамма-функция, интеграл Ганкеля по петле 54—55
Гамма-функция, интеграл Похгаммера по петле 56
Гамма-функция, интегралы Эйлера 47 53
Гамма-функция, история 64
Гамма-функция, минимум 57
Гамма-функция, особые точки 49
Гамма-функция, предельная формула Эйлера 50
Гамма-функция, представление в виде произведения 51
Гамма-функция, разложение в z = 1 88
Гамма-функция, рекуррентная формула 48
Гамма-функция, формула отражения 52
Гамма-функция, формула удвоения 52
Гамма-функция, формула умножения 52
Ганкель 54 172
Ганкеля разложения 304
Ганкеля разложения, оценки остатка 341—344
Ганкеля функции 303
Ганкеля функции полуцелого порядка 303
Ганкеля функции при больших значениях аргумента 304—306 341—345
Ганкеля функции, аналитическое продолжение 304
Ганкеля функции, вронскианы 309
Ганкеля функции, интегралы Ганкеля 308
Ганкеля функции, интегралы Зоммерфельда 308
Ганкеля функции, оценки 346
Ганкеля функции, рекуррентные формулы 308
Ганкеля функции, связь с функциями Бесселя 305 306 309
Ганс 292
Гаусс 205
Геллер 89
Гипергеометрическая функция 202 (см. также «Гипергеометрическое уравнение»)
Гипергеометрическая функция обобщенная 213 240
Гипергеометрическая функция поведение в z = 1 204 209—210
Гипергеометрическая функция при больших значениях аргумента 211
Гипергеометрическая функция смежная 206 225
| Гипергеометрическая функция, асимптотическое разложение при больших значениях параметров 206—207
Гипергеометрическая функция, зависимость от параметров 203
Гипергеометрическая функция, интеграл Похгаммера по петле 206
Гипергеометрическая функция, интегральные представления 204 206
Гипергеометрическая функция, история 240—241
Гипергеометрическая функция, квадратичное преобразование 212
Гипергеометрическая функция, особые точки 203
Гипергеометрическая функция, производные 206
Гипергеометрическая функция, связь с элементарными функциями 203 205
Гипергеометрический ряд 202
Гипергеометрическое уравнение 198
Гипергеометрическое уравнение обобщенное 213
Гипергеометрическое уравнение, второе решение при с = -1, -2, ... 212—213
Гипергеометрическое уравнение, формулы связи для решений 209—212
Главное значение интеграла 58 59
Гобсон 234 241
Грин 291 292
Гудвин 63
Гудвина — Стейтона интеграл 63 150
Де Брейн 40 46 177
Де Кок 138
Дебай 173 177
Джеффрис 263 291
Джоунс, Д.С. 137 175
Джоунс, Э.Л. 322
Дзета-функция 84—88
Дигамма-функция 56
Дифференциальные уравнения см. «Связи формулы» «Иррегулярные «ЛГ-приближение» «Особые
Дифференциальные уравнения с параметром см. «Связи формулы» «ЛГ-приближение» «Особенности
Дифференциальные уравнения с параметром, асимптотические решения 259—264 266—269 287
Дифференциальные уравнения с параметром, голоморфность решений 185 187 302
Дифференциальные уравнения с параметром, непрерывность решений 183 185
Дифференциальные уравнения с параметром, нули решений 270—273
Дифференциальные уравнения с параметром, оценки остатков для асимптотических решении 259—261 206
Дифференциальные уравнения с параметром, собственные знамения 274 292
Дифференциальные уравнения с параметром, собственные решения 274 276
Дифференциальные уравнения с параметром, собственные решения функции 274
Дифференциальные уравнения с простым полюсом 266—270 (см. также «Особые точки дифференциальных уравнений»)
Дифференциальные уравнения с тремя особыми точками 199
Дифференциальные уравнения, метод Коши для теорем существования 189
Дифференциальные уравнения, метод Пикара для теорем существования 181
Дифференциальные уравнения, метод последовательных приближений 181 208
Дифференциальные уравнения, нормальный ряд 285
Дифференциальные уравнения, нули решений 270—273
Дифференциальные уравнения, обыкновенная точка 189 195
Дифференциальные уравнения, подчиненные решения 197 254
Дифференциальные уравнения, решения доминирующие 197 254
Дифференциальные уравнения, решения линейная независимость 181 186 196
Дифференциальные уравнения, решения локальное поведение 242
Дифференциальные уравнения, решения неоднородные 182 346—351
Дифференциальные уравнения, решения нормальные 295
Дифференциальные уравнения, решения осцилляторного типа 243
Дифференциальные уравнения, решения субнормальные 296
Дифференциальные уравнения, решения фундаментальные 181—186
Дифференциальные уравнения, решения численно удовлетворительные 196—198 286
Дифференциальные уравнения, теоремы существования для действительных переменных 178—188 240
Дифференциальные уравнения, тождество Кейли 245
Дуги 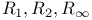 188 188
Евграфов, М.А. 111
Жордана неравенство 59
Задачи на собственные значения 274—278
Интегральная показательная функция 56—59 89
Интегральная показательная функция дополнительная 58
Интегральная показательная функция обобщенная 61
Интегральная показательная функция, асимптотическое разложение 146 291
Интегральная показательная функция, связь с гамма-функцией 65
Интегральные уравнения 278—281 292
Интегральный косинус 60 61
Интегральный косинус, асимптотическое разложение 91
Интегральный косинус, преобразование Лапласа 61
Интегральный логарифм 59 88
Интегральный синус 59
Интегральный синус, асимптотическое разложение 91
Интегральный синус, преобразование Лапласа 61
Интегрирование рядов асимптотических 34—35
Интегрирование рядов сходящихся 176
Иррегулярные особые точки 189 (см. также «Особые точки дифференциальных уравнений»)
Иррегулярные особые точки на бесконечности 195—196
Иррегулярные особые точки неоднородных уравнений 346—351
Иррегулярные особые точки, асимптотические решения 251—255 286—287 296—302
Иррегулярные особые точки, история 356
Иррегулярные особые точки, ЛГ-приближение 294
Иррегулярные особые точки, нормальные решения 295
Иррегулярные особые точки, оценки остатков для асимптотических решений 284 340 356
Иррегулярные особые точки, ранг 189 196
Иррегулярные особые точки, характеристическое значение 295
Иррегулярные особые точки, характеристическое уравнение 295
Казаринов 356
Калоджеро 268
Каратеодори 240
Карлеман 46
Карлини 291
Кельвин 137
Кельвина функции 84
Кертис 296
Клаузен 214
Кон 292
Коппель 259
Копсон 36 83 157 160 177
Кохран 322
Крамерс 201
Кронекера символ 60
Куммера функция 326 (см. также «Вырожденная гипергеометрическая функция»)
Лагерра полиномы 69 71 74
Лагерра полиномы, связь с вырожденными гипергеометрическими функциями 332
Лайнисс 137
Лангер 292
Ландау 15
Лаплас 107
Лапласа интегралы 92
Лапласа интегралы, аналитическое продолжение 141—142
Лапласа интегралы, асимптотическое разложение 92—95 139—143
Лапласа метод 107 113
Лапласа метод для контурных интегралов 158—162
Лапласа метод, история 137
Лапласа метод, оценки остатка 120 127 137 174—175
Лапласа метод, примеры 110—112 115—117 165—168
Лапласа метод, связь с методом стационарной фазы 128
Лапласа преобразование 146
Лапласа преобразование, абсцисса сходимости 147
ЛГ-приближение в особых точках 256—259 261—264 266
ЛГ-приближение для комплексных переменных 286
ЛГ-приближение, асимптотические свойства 251—264 286—287
ЛГ-приближение, история 291— 292
ЛГ-приближение, одно обобщение 266—270
ЛГ-приближение, оценки остатка 246 250 205—266 267 286
ЛГ-приближение, производная остатка по параметру 276
ЛГ-приближение, условие точности 246
ЛГ-функции 244
Лежандра полиномы 68 (см. также «Феррерса функции» «Лежандра
Лежандра полиномы при большом значении степени 112 165—167
Лежандра полиномы, дифференциальное уравнение 72
Лежандра полиномы, интеграл Лапласа 74
Лежандра полиномы, интеграл Шлефли 72
Лежандра полиномы, оценка 74
Лежандра полиномы, производящая функция 72
Лежандра полиномы, рекуррентные формулы 71 74
Лежандра полиномы, формула Родрига 69
Лежандра уравнение 214
Лежандра функции 215 221 «Присоединенное
Лежандра функции на разрезе 235
Лежандра функции порядка или степени, равных 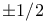 219—220 219—220
Лежандра функции при большом значении степени 263
Лежандра функции целого порядка 228 235
Лежандра функции, аналитическое продолжение 227
Лежандра функции, вронскианы 218
Лежандра функции, интеграл Гейне 234
Лежандра функции, интеграл Неймана 232
Лежандра функции, интегральные представления 221 224—228 230—232
Лежандра функции, история 240—241
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте