Авторизация
Поиск по указателям
Isham C. — Modern Differential Geometry for Physicists
Обсудите книгу на научном форуме Нашли опечатку?
Название: Modern Differential Geometry for PhysicistsАвтор: Isham C. Аннотация: These lecture notes are the content of an introductory course on modern, co-ordinate-free differential geometry which is taken by first-year theoretical physics PhD students, or by students attending the one-year MSc course, "Fundamental Fields and Forces" at Imperial College. The book is concerned entirely with mathematics proper, although the emphasis and detailed topics have been chosen bearing in mind the way in which differential geometry is applied to modern theoretical physics. This includes not only the traditional area of general relativity but also the theory of Yang-Mills fields, nonlinear sigma models and other types of nonlinear field systems that feature in modern quantum field theory. This edition of the text contains an additional chapter that introduces some of the basic ideas of general topology needed in differential geometry. A number of small corrections and additions have also been made. The volume is divided into four parts. The first provides an introduction to general topology, the second covers introductory co-ordinate-free differential geometry, the third examines geometrical aspects of the theory of Lie groups and Lie group actions on manifolds, and the fourth provides an introduction to the theory of fibre bundles. In the introduction to differential geometry the author lays considerable stress on the basic ideas of "tangent space structure", which he develops from several different points of view - some geometrical, others more algebraic.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1999Количество страниц: 306Добавлена в каталог: 23.11.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
233 81 162 226 11 160 142 218 5 9 62 125 272 48 204 154 180 127 143 78 105 250 94 94 9 159 171 150 98 116 130 180 233 162 150 65 68 229 74 123 123 133 5 74 121 254 191 63 24 97 99 98 142 4 26 24 101 248 171 223 16 24 224 98 204 192 34 26 219 4 188 229 79 222 188 5 5 110 135 142 142 171 171 137 135 135 219 126 53 5 5 5 15 34 234 95 75 218 233 4 8 135 80 127 263 133 121 269 87 34 (E, 202 a 146 A 5 A 6 a 19 a 18 Accumulation point 47 Adjoint map 162 Anti-homomorphism 152 Associated bundle 233 Associated bundle, automorphism group of 239 Associated bundle, local isomorphism between pair of 237 Associated bundle, map between pair of 237 Associated bundle, trivial 237 Bd(A) 12 Bianchi identity 274 Billiard-ball hairy 101 Boolean algebra 20 42 Boundary of a set 12 Boundary point 12 31 Bundle 202 Bundle 204 Bundle base space 202 Bundle cross-section of see "Cross-section" Bundle etale 212 Bundle fibre 204 Bundle fibre over x 202 Bundle G 220 Bundle isomorphism between a pair of 215 Bundle local isomorphism between a pair of 215 Bundle locally trivial 216 Bundle M-map 215 Bundle map 214 Bundle map, composition of pair of 215 Bundle normal 210 Bundle normal, of an embedding 249 Bundle of tensors 236 Bundle product 204 Bundle projection map of 202 Bundle pull-back 217 Bundle restriction to subset of base space 213 Bundle sub 213 Bundle total space 202 Bundle trivial 216 Bundle universal 219 228 232 Canonical 110 Cartan structural equation 272 Cartan — Maurer equation 173 Cartan — Maurer form 173 257 Cartesian product 6 36 64 Characteristic class 219 231 Closed set 13 31 35 Closure 53 Collection of subsets coarser than 26 Commutation relations affine 111 Compact space 47 Connection affine sum of pair of 256 Connection local representative of 256 Connection principal bundle in 254 Coordinate chart 61 Coordinate chart, atlas of 62 Coordinate chart, domain of 61 Coordinate functions 63 coordinates 63 Cotangent bundle 123 Cotangent space 123 Cotangent vector 123 Covariant derivative 269 270 Covering space 210 Cross-section 200 207 241 Cross-section, associated bundle of 246 Cross-section, local representative of 247 Cross-section, principal bundle of 230 Cross-section, product bundle of 207 Cross-section, pull-back of 218 Cross-section, tangent bundle of 98 Curvature two-form 272 Curve, definition of 73 Curve, horizontal lift of 263 Curve, tangent pair of 73 d(x,y) 6 deRham complex 141 171 DeRham's theorem 217 Derivation at a point 80 Derivation of the ring 99 Derivation, components of 84 df 131 Diff( 70 Diffeomorphism, definition of 70 Diffeomorphism, group of 70 224 229 Diffeomorphism, one-parameter group of 111 Differentiable manifold 62 Differentiable manifold, complex 63 Differentiable manifold, infinite-dimensional 63 Differential structure 62 Directed set 46 Directional derivative 75 Dual vector space 121 Dual vector space, dual basis of 121 Dual vector space, dual map between pair of 121 E( 204 Eilenberg — MacLane space 228 Equivalence exact sequence 255 exp A 165 Exponential map 165 Ext(A) 12 Exterior derivative covariant 272 Exterior derivative, function of 131 Exterior of a set 12 Exterior point 12 31 f:A 6 Filter base 29 47 50 Filter base, convergence with respect to 30 Filter, definition of 29 Filter, subbase 31 Filter, ultra 45 Finer than 26 First countable space see "Topology first Function 69 Function continuous 49 Function diagonal 95 Function differentiable 70 Function distance 5 Function equivariant 178 Function inverse set 48 Function smooth 70 Function, homotopic pair of 145 218 Function, local representative of 69 G-product 232 Gauge group 16 224 229 231 258 Gauge orbit 16 Gauge transformation 224 226 239 258 GL(n, 153 GL(n, 152 Gribov effect 231 Group action 52 Group action, orbit of 52 Group Lorentz 157 Group, action on a set 175 Group, action on a set, free 179 Group, action on a set, kernel of 179 Group, action on a set, orbit of 180 Group, action on a set, orbit space of 182 Group, action on a set, stability group of 180 Group, action on a set, transitive 179 Group, adjoint representation of 168 Group, cohomology 201 217 219 229 232 242 Group, general linear, complex 284 Group, general linear, real 152 Group, holonomy 267 Group, homotopy 228 229 242 246 Group, left translation of 150 Group, orthogonal 155 Group, orthogonal special 157 Group, partial 113 Group, right translation of 150 Group, special linear 154 Group, special unitary 157 Group, spin 225 Group, topological 151 Group, unitary 157 Hausdorff space see "Topology Hausdorff" Heyting algebra 42 Homeomorphism 51 Homotopic functions see "Function homotopic Hopf bundle 222 hor( 255 Horizontal subspace 268 Instanton 201 222 226 243 Int(A) 12 Integral curve see "Vector field integral Interior of a set 12 Interior point 12 31 Intuitionistic logic 42 Isotropy group see "Group action stability Jacobi identity 103 Jacobian matrix 88 K( 228 Kaluza — Klein theory 201 Klein bottle 205 L(G) 158 Lattice a topology as an example 40 Lattice anti-atomic 45 Lattice atomic 44 Lattice complete 19 41 Lattice distributive 19 41 Lattice example of closed linear subspaces of a Hilbert space 22 Lattice structure on space of topologies 43 Lattice, definition of 19 Lattice, null element in 19
Реклама
 |
|
О проекте
|
|
О проекте



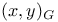
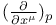 f
f 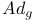
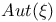
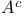
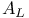
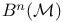
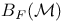
![$C([a,b],\mathds{R})$](/math_tex/8f7586121b509ceb78994bec1d8e733582.gif)

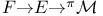
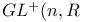 )
) 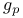
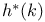
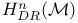
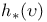
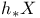
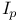
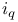
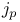
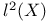
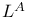
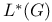
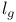
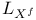
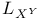
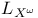
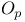
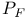
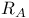
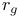
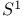
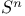
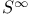
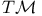
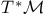
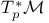
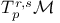
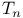
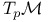
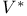
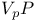
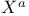
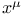
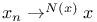
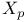
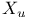
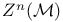
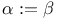
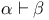

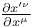
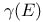
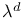
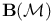
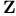
![$\mathcal{F}([a,b],\mathds{R})$](/math_tex/eb9d48e7e996cd6c19213928b58dea3d82.gif)
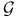
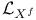
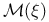
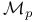
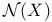
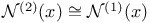
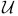 F
F 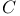
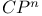
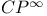
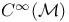
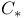
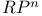
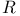
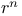
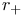
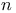 -form
-form 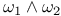
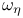
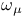
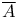
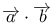
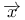
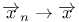
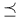
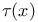
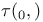
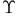
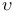 (f)
(f) 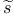 (x)
(x) 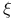 [F]
[F] 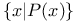
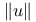
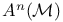
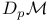
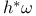
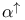
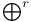 V
V 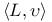
 )
)  b
b  B
B  B
B  b
b  b
b 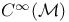
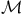 )
)  B
B 
 )
)  ,n)
,n)