Авторизация
Поиск по указателям
Fritsch R., Piccinini R. — Cellular Structures in Topology (Cambridge Studies in Advanced Mathematics 19)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Cellular Structures in Topology (Cambridge Studies in Advanced Mathematics 19)Авторы: Fritsch R., Piccinini R. Аннотация: This book describes the construction and the properties of CW-complexes. These spaces are important because firstly they are the correct framework for homotopy theory, and secondly most spaces that arise in pure mathematics are of this type. The authors discuss the foundations and also developments, for example, the theory of finite CW-complexes, CW-complexes in relation to the theory of fibrations, and Milnor's work on spaces of the type of CW-complexes. They establish very clearly the relationship between CW-complexes and the theory of simplicial complexes, which is developed in great detail. Exercises are provided throughout the book; some are straightforward, others extend the text in a non-trivial way. For the latter; further reference is given for their solution. Each chapter ends with a section sketching the historical development. An appendix gives basic results from topology, homology and homotopy theory. These features will aid graduate students, who can use the work as a course text. As a contemporary reference work it will be essential reading for the more specialized workers in algebraic topology and homotopy theory.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1990Количество страниц: 336Добавлена в каталог: 22.11.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
20 (Geometric) standard n-simplex 93 2-category 133 Absolute neighbourhood retract (ANR) 281 Acyclic fibration 178 Acyclic models 286 Adams, J.F. (1930-1989) 88 Addition law (L3) 263 Adjoint (of a simplicial map) 157 Adjoint functor generating principle 303 Adjunction of n-cells 12 Adjunction space 258 Admissible pair (of maps) 292 Affine embedding 91 Affinely independent 89 Alder, M.D. 127 Alexander, J.W. (1888-1971) 131 Alexandroff, P.S. (1896-1983) 131 Allaud, G. 272 Anodyne extension 172 Approximation 68 Associated simplicial set (to an ordered simplicial complex) 152 Attaching (simplicial) 144 Attaching map 12 259 Attaching space 258 Axiom of Choice 31 Axiom of Countable Choice 31 Axiom of multiple choice 31 Ball 1 Barratt, M. 131 222 Barycentre 92 Barycentric coordinates 90 Barycentric refinement of a covering 248 Barycentric subdivision 111 Base (of a euclidean cone) 92 Base (of a Kan fibration) 171 Base space (of a fibration) 255 Based homotopy 286 Based map 286 Borges, C.R. 33 304 305 Borovikov, V. 131 Borsuk, K. (1905-1982) 282 283 Boundary (of standard p-simplex) 142 Bouquet of spheres 18 Bourbaki, N. 252 303 Brouwer theorem 300 302 Brown, R. 54 88 242 251 252 259 266 271 279 298 299 Canonical CW-structure of a ball 24 Canonical simplicial map 200 Cantor set (middle third set) 224 252 Carrier 23 90 98 112 Cartesian product 241 Category of finite ordinals 132 Category of n-ads with type of CW-n-ads 230 Category of presimplicial sets PSiSets 165 Category of simplices functor 141 Category of simplicial sets SiSets 139 Category of small categories 141 Category of spaces with type of CW-complexes TCW 223 Category of topological spaces Top 241 Category of weak Hausdorff k-spaces wHk(Top) 243 Cauty, R. 33 Ceder, J.G. 250 Cell (closed, open, regular) 11 Cell complex 51 Cell path-connected 41 Cell subcomplex 51 Cellular approximation theorem 73 Cellular map 56 Cellular map of (relative) CW-complexes 56 Cellular partial map 62 Chain complex functor 284 Characteristic map 12 259 Classifying set 192 Closed cofibration 251 Closed n-cell 11 Closed regular n-cell 11 Closure finite 40 52 Cogluing theorem 270 Collar 20 Collaring 19 Columbus, G. (1451-1506) 2 Compact-open topology 241 Compactly closed 242 Compatible sequence of maps 273 Complementary face 89 Complete weak homotopy equivalence 231 Composable (pair) 139 Cone 269 Cone (Euclidean) 92 Cone (of a presimplicial set) 167 Cone functor (of presimplicial sets) 167 Connected simplicial set 194 Convenient 242 Convex covering 118 Convexely independent subfamily 95 Coproducts of CW-complexes 57 Coreflective subcategory 152 Cosimplicial map 146 Cosimplicial object (in a category) 138 Cosimplicial set 146 Countable CW-complex 40 Countable family 248 Countable simplicial complex 121 Covering 248 Covering dimension 299 Covering projection 256 Covering space 256 Covering transformation 291 Cross-section 270 cube 96 Curtis, E.B. 220 CW-complex 22 CW-complex of finite dimension 46 CW-complex of finite type 40 CW-n-ad 230 CW-structure 22 Degeneracy operator 135 Degenerate simplex 144 Degree 90 Determined (by a family of subspaces) 246 Diameter (of a geometric simplex) 91 Dimension (of a CW-complex) 46 Dimension (of a Euclidean complex) 100 Dimension (of a minimal pair) 149 Dimension (of a simplex) 139 Dimension (of a simplicial set) 146 Dimension (of an operator) 132 Dimension and embedding 46 Directly equivalent pairs 149 Dold, A. 131 272 Domination 288 Dowker, C.H. (1912-1982) 87 131 Dugundji extension theorem 281 Dugundji, J. (1919-1965) 54 242 248 249 253 302 Dunce hat 152 Dydack, J. 225 239 Dyer, E. 55 267 Eckmann, B. 292 EDGE 89 Eggs of Columbus 2 Eilenberg — MacLane spaces 87 193 Eilenberg — Zilber lemma 145 Eilenberg — Zilber property 149 Eilenberg, S. 55 87 131 197 220 221 267 285 286 ELCX-n-ad 232 ELCX-space 118 ELCX-subspace 119 Elementary degeneracy operator 135 Elementary expansion 65 Elementary face operator 133 Engelking, R. 54 299 300 302 Equi locally convex space (ELCX-space) 118 Equi locally convex structure (ELCX-structure) 118 Equi locally convex subspace (ELCX-subspace) 119 Equiconnecting homotopy 118 Euclidean complex 97 Euclidean realization of a simplicial complex 122 Evaluation map 241 Expanding sequence 273 Exponential law 243 Extension functor 212 Face (of a simplex) 89 110 Face operator 133 Fat realization 166 Fibration 171 254 Fibre 143 Fibre (of a fibration) 255 Fibre homotopic (simplices are-) 181 Fibre homotopy 255 Fibre homotopy (of simplices) 181 Fibre homotopy equivalence 255 Fibre map 255 Figure-eight 287 Filling of horns 171 Filtration (of a space) 22 Final topology 246 Finite CW-complex 40 Finite dimensional CW-complex 46 Finite dimensional simplicial complex 121 Finite euclidean complex 97 Finite ordinals (category) 132 Finite presentation (of groups) 81 Finite simplicial complex 121 Finite type (CW-complexes) 40 Finney, R.L. 127 Folklore, J. 54 Forgetting degeneracies 165 Fox, R.H. (1913-1973) 131 Frechet space 26 27 55 Freudenthal, H. 54 Freyd, P. 221 Fritsch, R. 197 198 221 222 Function n-ad 234 Fundamental group 287 Fundamental group of a CW-complex 78 Fundamental groupoid 298 Gabriel, P. 198 220 221 222 247 284 285 304 Gale, D. 242 Generator (of a simplicial set) 144 Geoghegan, R. 225 239 Geometric realization 112 139 Geometric realization (of a simplicial map) 121 140 Geometric realization functor 121 140 153 Giever, J.B. 221 Global set (of a Euclidean cone) 92 Gluing theorem 266 Groupoid 298 Gugenheim, V. 220 Hanai, S. 27 Hanner, O. 131 Hauptvermutung 112 131 Heath, P.R. 271 304 Hilbert cube 48 302 Hilton, P.J. 170 283 290 291 292 Homology 284 Homology functor 284 Homotopy addition theorem 297 Homotopy equivalence of pairs 278 Homotopy extension property 250 Homotopy groups 287 Homotopy groups of maps 292 Homotopy lifting property 254 Homotopy sequence of a fibration 297 Homotopy sequence of maps 293 Homotopy type 266 Horizontal composition law (L1) 262 Horn 170 Hu, S. 54 Hurewicz fibration 185 255 Hurewicz, W. (1904-1957) 301 Hyman, D.M. 54 Identity operators 133 Increasing the connectivity of maps 83 Induced 142 143 Infinite ball 2 Infinite collar 27 Infinite projective space 25 Infinite simplex 114 Infinite sphere 2 Initial topology 248 Interior (of a simplex) 89 Invariance of domain (theorem) 302 inversion 6 Isomorphic simplicial complexes 111 k-horn 170 k-ification 242 k-simplex 89 110 k-space 242 Kamps, H. 271 287 Kan condition 221 Kan fibration 171 Kan set 172 Kan, D.M. 197 198 220 221 222 303 Kaplan, S. 249 Kelley, J.L. i 245 Kodama, Y. 221 Kolmogorov, A.N. (1903-1989?) 131 Kuratowski — Wojdyslawski embedding theorem 281 Lamotke, K. 197 220 221 222 284 Latch, D.M. 197 221 LEC-spaces 253 Lefschetz, S. (1884-1972) i Lens space 169 170 Lewis, L.G., jr 266 Lifting property 254 Lifting theorem 291 Lillig, J. 252 Lindeloef space 50 Link 101 Local vertex ordering 111 Locally contractible space 28 Locally equiconnected spaces (LEC) 253 Locally finite CW-complexes 40 Locally finite family 248 Locally finite partition of unity 249 Locally finite simplicial, complex 121 Locally path-connected 29 Locally trivial map 163 271 Locally trivial simplicial map 143 Loop space 256 Lundell, A.T. 51 55 62 131 m-connected map 295 M-equivalence 295 MacLane, S. i 87 287 220 283 Map (simplicial) induced from 143 Map induced from 258 Mapping cone 269 Mapping cylinder 264 Mapping space 241 Mapping track 270 Mardesic, S. 281 Massey, W.S. 88 299 Mather, M.R. 131 May, J.P. 220 McCord, M.C. 244 247 Menger — Noebeling theorem 302 Menger, K. (1902-1985) 302 Metric topology 113 Metzler, W. 131
Реклама
 |
|
О проекте
|
|
О проекте



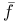 -collar
-collar