|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bonahon F. Ч Low-Dimensional Geometry: From Euclidean Surfaces to Hyperbolic Knots (Student Mathematical Library: Ias Park City Mathematical Subseries) |
|
|
 |
| ѕредметный указатель |
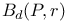 , a ball in a metric space 4 , a ball in a metric space 4
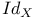 , the identity map of X 357 , the identity map of X 357
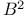 , the disk model for the hyperbolic plane 36 36Ч39 43 44 101 158Ч160 209 212 216 223 , the disk model for the hyperbolic plane 36 36Ч39 43 44 101 158Ч160 209 212 216 223
 , the set of all complex numbers 356 361Ч364 , the set of all complex numbers 356 361Ч364
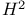 , the hyperbolic plane 11 11Ч46 , the hyperbolic plane 11 11Ч46
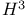 , the 3-dimensional hyperbolic space 227 227Ч240 , the 3-dimensional hyperbolic space 227 227Ч240
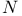 , the set of all positive integers 356 , the set of all positive integers 356
 , the set of all rational numbers 356 , the set of all rational numbers 356
 , the set of all real numbers 356 , the set of all real numbers 356
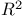 , the euclidean plane 1Ч10 357 , the euclidean plane 1Ч10 357
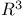 , the 3-dimensional euclidean space 4 357 , the 3-dimensional euclidean space 4 357
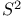 , the 2-dimensional sphere 47 , the 2-dimensional sphere 47
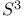 , the 3-dimensional sphere 343 351 , the 3-dimensional sphere 343 351
 , the set of all integers 356 , the set of all integers 356
Absolute value 23 362
Action of a group 185 185Ч205 248
Adjacent tiles 137 137Ч146 261
Alexander, James Waddell II (1888-1971) 318
Antilinear fractional map 27 27Ч33 38 186 231Ч235
Antipodal points 49 102
Arc length see "Length"
Area 131
Area, hyperbolic area 43 43Ч44
Area, spherical area 53 182
Ball, ball in 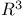 5 344 5 344
Ball, ball in a metric space 4 42Ч43 68Ч79 240 262
Ball, ball model for the hyperbolic space 236 240
Belong to 355
Bijection 5 90 185 357
Bijective 357
Bonahon, Francis iii
Bonnet, Pierre Ossian (1819-1892) 131
Boundary, boundary of a manifold 348
Boundary, boundary point 152
Bounded 62 81 152 152 161
Brock, Jeffrey F. 283
Bromberg, Kenneth W. 282
Busemann, Busemann function 178 183
Busemann, Busemann, Herbert (1905-1994) 178
Canary, Richard D. 283
Cannon, James W. 302
Canonical tile 143 143Ч146
Cauchy, Cauchy sequence 135 182
Cauchy, Cauchy, Augustin (1789-1857) 182 211
Cayley, Arthur (1821-1895) 45
Center, center of a horocircle 172 214
Center, center of a horosphere 234
Cerf, Jean 318
circle 5 17Ч22 32Ч33 38 48 85Ч87 172 207Ч212 230 288 317
Circle, great circle 48 129
Circle, great circle arc 49 50Ч51
Closed, closed curve 49 316
Closed, closed geodesic 49 127Ч129 204
Closed, closed subset 62 80 152 152Ч154 250Ч251 257Ч258 286
Compact metric space 150 150 154 182 203 251 348
Companion knot 321
Complement 356
Complement, knot complement 293Ч313 319Ч340 352Ч354
Complete, complete geodesic 21
Complete, complete metric space 135 147Ч155 174 182 183 203 230 260 311 322 325 341 346 348
Complex number 6 11 23 361 361Ч364
Complex number, complex conjugate 6 23 44 362
Complex number, complex exponential 242 364 362 364
composition 6 15 28 42 51 52 185 186 357
Cone 86
Cone, surface with cone singularities 87 125Ч126 136 192 205 342
conjugate see "Complex conjugate"
Connected 64 341
Continued fraction 224
Continuous function 4 8 9 61 90 151 302 360
Convergence 4 135 147Ч155 360
Convergence, limit at infinity 361 360Ч361
Convergence, toward infinity 361 360Ч361
Convex, euclidean polygon 62
Convex, hyperbolic polygon 82
Convex, spherical polygon 82
Crossratio 44Ч45
Differential map 29 29Ч38 40 49Ч50 229Ч230 317
Dihedral angle 235 259 259Ч265 290
Dihedron 235
Dirichlet, Dirichlet domain 198 197Ч201
Dirichlet, Lejeune Dirichlet, Gustav (1805-1859) 198
Discontinuity domain 286Ч287
Discontinuous group action 189 189Ч197 203Ч205 248 254 260 268 280Ч283 286 313
Discrete walk 58 58Ч60 69Ч79 85Ч86
Disjoint sets 356
Disk, disk in the plane 5
Disk, disk model for the hyperbolic plane 36 36Ч39 43 44 101 158Ч160 209 212 216 223
Disk, disk sector 72 86 205
Distance, distance function 3
Distance, euclidean distance 2 1Ч3 8 340
Distance, hyperbolic distance 12 12Ч14 37 39 44 45 228
Distance, signed distance 218Ч220 253 253Ч254
Distance, spherical distance 48 343
Domino diagram 225 291
Dumas, David 282
Dunne, Edward G. xv
Earle, Clifford J. 280
Edge of a hyperbolic polyhedron 258 258Ч265
Edge of a polygon 61 61Ч83 257
Edge, edge cycle 172 172Ч181
Element of a set 355
Elliptic isometry 41 239 240
Empty set 355
Epstein, David B.A. 340
Equivalence class 84
Equivalence relation 84
Essential surface 343Ч346
Essential surface, essential Klein bottle 345
Essential surface, essential projective plane 344
Essential surface, essential sphere 344
Essential surface, essential torus 344
Euclidean, euclidean distance 2 3 340
Euclidean, euclidean geodesic 3 21
Euclidean, euclidean isometries 5Ч7 39
Euclidean, euclidean length 2 48
Euclidean, euclidean metric 67 340
Euclidean, euclidean norm 33
Euclidean, euclidean plane 1Ч10
Euclidean, euclidean polygon 61 61Ч66 183
Euclidean, euclidean space 340 349
Euclidean, euclidean surface 67 89Ч97 103Ч104 341 343
Euclidean, euclidean triangle 125
Euler, Euler characteristic 131
Euler, Euler exponential notation 6 362
Euler, Euler, Leonhard (1707-1783) 131 362
Exceptional fiber 347
Exponential, complex exponential 242 364 362Ч364
Exterior point 152
Face of a polyhedron 258 257Ч265 334Ч340
Farey, crooked Farey tessellation 243 241Ч247 265Ч265 279 291Ч297
Farey, Farey circle packing 210 207Ч226
Farey, Farey series 223
Farey, Farey sum 209
Farey, Farey tessellation 210 207Ч226
Farey, Farey, John (1766-1826) 210
Fiber 347
Fibration see "Seifert fibration"
Fields medal 322 350
Figure-eight knot 303 293Ч313 352 353
Finite volume 324
fix 358
Fixed point 358
Ford, Ford circles 212
Ford, Ford domain 331 326Ч340
Ford, Ford, Lester Randolph (1886-1967) 212 340
Free group action 192 264 280Ч282 297 352
Fuchs, Lazarus Immanuel (1833-1902) 284
Fuchsian group 255 252Ч257 280 283Ч284
Fuchsian group, fuchsian group of the first type 256
| Fuchsian group, fuchsian group of the second type 256
Fuchsian group, twisted fuchsian group 288
Function 357
Fundamental domain 192 185Ч205 259 259Ч269 296Ч298
Gauss Ч Bonnet formula 131
Gauss, Johann Carl Friedrich (1777-1855) 131
Generate transformation group generated by bijections 135Ч136 186 194 260
Genus 97 129
Geodesic 21
Geodesic, closed geodesic 49 127Ч129 204
Geodesic, complete geodesic 21
Geodesic, euclidean geodesic 3 21
Geodesic, hyperbolic geodesic 17 22 230
Geodesic, spherical geodesic 49Ч51
Geometric structure 349
Gordon, Cameron McA. 340
Great circle 48 129
Great circle arc 49
Group 185 185Ч205
Group, abstract group 202
Group, fuchsian group 255 252Ч257 280 283Ч284
Group, group action 185 185Ч205
Group, group of isometries 186
Group, isometry group 186
Group, kleinian group 248 241Ч302 326Ч340
Group, tiling group 136 135Ч184 212Ч222 259
Group, transformation group 185 185Ч205
Haken, Wolfgang 350
Hamilton, Richard S. 350
Haros, C. 211
Hatcher, Allen E. 318
Hiatt, Christopher xvi
Homeomorphic 90
Homeomorphism 41 90 91 96Ч98 126 129 130 182 270 288 303Ч311 317Ч319 325
Homogeneous 7 15Ч16 34Ч36 49Ч50 128 129 230 349
Homothety 15 28 40 228 239 286
Horizontal translation 15 28 41 228 239
Horocircle 172 172Ч181 214Ч222 290
Horocycle 172
Horocyclic isometry 172 172Ч176 221Ч222
Horodisk 178 178Ч180 256
Horosphere 234 234Ч235 260Ч265 268 298 331Ч332
Howe, Roger E. xv
Hyperbolic, hyperbolic area 43 43Ч44
Hyperbolic, hyperbolic disk 42
Hyperbolic, hyperbolic distance 12 12Ч14 37 39 44 45 228
Hyperbolic, hyperbolic geodesic 17 22 230
Hyperbolic, hyperbolic isometry 14Ч17 25 23Ч27 40 232 231Ч231 234 238 239
Hyperbolic, hyperbolic knot 322 322Ч340
Hyperbolic, hyperbolic length 11 17Ч22 33Ч34 227 230
Hyperbolic, hyperbolic metric 12 12Ч14 37 39 44 45 82 228
Hyperbolic, hyperbolic norm 33 33Ч36 228 229
Hyperbolic, hyperbolic plane 11 11Ч46 234
Hyperbolic, hyperbolic polygon 80
Hyperbolic, hyperbolic reflection 15 240
Hyperbolic, hyperbolic rotation 40
Hyperbolic, hyperbolic space 227 227Ч240 349
Hyperbolic, hyperbolic surface 82 102 341Ч343
Hyperbolic, hyperbolic triangle 43 98 125 130
Hyperbolic, hyperbolic volume 240 353
Ideal, ideal polygon 116
Ideal, ideal vertex 116 170 170Ч180 257 258 257Ч265
identity map 185 357
Image 357
Imaginary part 11 362
Infimum (pl. infima) 359 358Ч360
Infinite limit 361 360Ч361
Infinity, limit at infinity 361 360Ч361
Infinity, vertex at infinity 170 170Ч180 257 258 257Ч265
Injective 357
Interior, interior of a manifold 348
Interior, interior point 152
Intersection 356
Inverse map 185 357
Inversion across a circle 16 16Ч17 28 28 42
Inversion across a sphere 229 237
Isometric, isometric extension 233 231Ч233 236
Isometric, isometric group action 186
Isometric, locally isometric 67
Isometry 5
Isometry, elliptic isometry 41 239
Isometry, euclidean isometries 5 7 39
Isometry, group of isometries 186
Isometry, horocyclic isometry 172 172Ч176 221Ч222
Isometry, hyperbolic isometry 14Ч17 25 23Ч27 40 232 231Ч234 238 239
Isometry, isometry group 186
Isometry, loxodromic isometry 40 239
Isometry, parabolic isometry 41 239 327
Isometry, spherical isometries 50
Isomorphic knots 317
Isotopic knots 316
Isotopy 316
Isotropic 7 34Ч36 49Ч50 230 349
Jaco, William H. 321 350
Jacobian 238 317
Johannson, Klaus 321 350
Klein, Klein bottle 95 93Ч95 128 341
Klein, Klein bottle, essential Klein bottle 345
Klein, Klein, Felix (1849-1925) 45 95 284
Kleinian group 248 241Ч302 326Ч340
Kneser, Hellmuth (1898-1973) 350
Knot 316
Knot, companion knot 321
Knot, figure-eight knot 303
Knot, hyperbolic knot 322 322Ч340
Knot, knot complement 293Ч313 319Ч340 352Ч354
Knot, satellite knot 321
Knot, torus knot 319
Knot, trefoil knot 319
Knot, unknot 317
Length, euclidean length 2 48
Length, hyperbolic length 11 17Ч22 33Ч34 227 230
Length, length in a metric space 3 9 87 127
Length, length of a discrete walk 58
Length, length of a sequence 135 147Ч155
LIMIT 4 135 147Ч155
Limit, limit at infinity 361 360 361
Limit, limit point 248
Limit, limit set 248 247Ч252 255Ч256 270Ч279 299Ч302
Linear fractional map 27 27 33 38 186 231Ч235
Linear groups 202
Listing, Johann Benedict (1808-1882) 104
Little, Charles N. 337
Locally finite 134 145 197 259 261 333 334
Locally isometric 67 82 83
Loxodromic isometry 40 239
Luecke, John 340
Manifold 340 340Ч351
MAP 357
Marden, Albert 296
Maximum (pl. maxima) 358 358Ч360
McMullen, Curtis T. 322
Metric 3
Metric, euclidean metric 67 340
Metric, hyperbolic metric 12 12Ч14 37 39 44 45
Metric, metric function 3
Metric, metric space 3 3Ч5 58Ч61 134Ч135 150Ч155
Metric, path metric 9 63 81 82
Metric, product metric 8 344
Metric, quotient metric 61 58 61 141Ч143 187Ч189
Metric, spherical metric 48 343
Milnor, John W. 350
Minimum (pl. minima) 358 358Ч360
Minsky, Yair N. 282 283
Moduli space 342
Modulus (pl. moduli) 23 362
Moebius strip 341
Moebius, Moebius group 237
Moebius, Moebius strip 104 103Ч104
Moebius, Moebius transformation 237
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



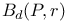 , a ball in a metric space
, a ball in a metric space 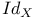 , the identity map of X
, the identity map of X 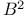 , the disk model for the hyperbolic plane
, the disk model for the hyperbolic plane  , the set of all complex numbers
, the set of all complex numbers 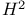 , the hyperbolic plane
, the hyperbolic plane 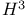 , the 3-dimensional hyperbolic space
, the 3-dimensional hyperbolic space 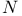 , the set of all positive integers
, the set of all positive integers  , the set of all rational numbers
, the set of all rational numbers  , the set of all real numbers
, the set of all real numbers 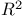 , the euclidean plane
, the euclidean plane 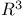 , the 3-dimensional euclidean space
, the 3-dimensional euclidean space 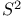 , the 2-dimensional sphere
, the 2-dimensional sphere 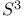 , the 3-dimensional sphere
, the 3-dimensional sphere  , the set of all integers
, the set of all integers