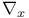|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Snygg J. Ч Clifford algebra: a computational tool for physicists |
|
|
 |
| ѕредметный указатель |
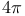 periodicity of rotation operator 11Ч12 periodicity of rotation operator 11Ч12
1-forms 50 51
1-vector 5 42
2-vector 5
3-vector 5
4-momentum 37
4-momentum, conservation of 40
Abramowitz, Milton 191
Abstract indices 89
Adair, Thomas W. III 38
Adams, John Couch, prediction of Neptune 126
Adler, Ronald 217
Albert, Abraham Adrian 308
Algebra 5 42
Algebra, associative 42
Algebra, generators of 295
Anderson, Carl D., discovery of positron 181
Angle of precession for spinning top 14
Areal velocity 118
Associated Legendre functions 191
Associative algebra 42
Atiyah, Michael F. 294
Axial vector (pseudo-vector) 8
Bazin, Maurice 217
Bianchi identity for a Yang Ч Mills field 145
Bianchi identity in computation of Kerr metric 280Ч282
Bianchi identity, proof of 323Ч324
Biorthogonal bases for a vector space 47Ч48 70Ч74
Bivector, simple unit space-space 309
Bivector, simple unit space-time 309Ч310
Bohr radius 214
Bohr, Niels, criticism of Dirac's antiparticle 181
Bolker, Ethan 11
Boost 29Ч32
Bott, Raoul H. 294
Bound charges and currents 141Ч142
Boyer Ч Lindquist coordinates 246 248
Boyer, Robert H. 242
c-Hermitian 171
c-unitary Clifford numbers 171 301Ч306
c-unitary groups, classification of 301Ч306
Canonical form for solutions of Dirac's equation 185Ч189
Cartan, Elie, theorem on rotations and reflections 9
Chandrasekhar, Subrahmanyan 247
Charge conjugate of a Clifford number 178Ч179 185 202
Christoffel symbols 76Ч78 86Ч88
Christoffel symbols, formula for 87
Christoffel symbols, transformation of 88
Clifford algebra, for 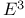 3Ч5 3Ч5
Clifford algebras 3Ч5 41Ч42 288
Clifford algebras for pseudo-Euclidean spaces 43
Clifford algebras, complex 42 288
Clifford algebras, construction of 288Ч294
Clifford algebras, real 42 288
Clifford algebras, singular 76
Clifford algebras, universal 44 288
Clifford number 5 42
Clifford number, complex 42
Clifford number, index free 88
Clifford number, real 42
Clifford number, simple 309
Clifford reverse 57Ч58 307
Clifford, William Kingdon 41
Closed p-vector 134
Codifferential operator 130Ч137
Comma notation 88
Commutator coefficients 91Ч92
Complex Clifford algebras 42 288
Complex Clifford number 42
Complex conjugate of a Clifford number 171
Complex reverse of a Clifford number 171
Complex scalar product for Clifford numbers 171
Components of a contravariant tensor of order one 51
Components of a covariant tensor of order one or two 51
Components of a mixed tensor of order two 51Ч52
Confluent hypergeometric function 208Ч211
Conformal tensor 250Ч251
Conjugate, complex, of a Clifford number 171
Connection coefficients 90Ч91
Connections for Yang Ч Mills field 144
Contracted Christoffel symbol 132Ч133
Contracted tensor 90
Contravariant tensor, components of 51
Convection current 175
Converse of Poincare lemma 133Ч134
Coordinate system of Dirac matrices 45
Cosmological constant 149
Covariant derivative of a Dirac matrix 89Ч90
Covariant derivative of a tensor component 89
Covariant tensor, components of 51
Cowan, Clyde, discovery of neutrino 37
Current 1-vector 139Ч141
Curvature 2-form 101
Curvature 2-form as an infinitesimal rotation operator 104Ч110
Cyclotron and Migma chamber 154Ч162
Cylindrical coordinates 53
Degenerate metric 104
Derivative operator 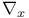 86Ч89 86Ч89
Derivative operator 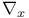 for m-dimensional spaces embedded in n-dimensional spaces 75Ч79 for m-dimensional spaces embedded in n-dimensional spaces 75Ч79
Dieudonne, Jean, theorem on rotations and reflections 9
Differential forms 50Ч51
Dipole, electric and magnetic of free electron 184
Dirac matrices 41
Dirac matrices, coordinate system of 45
Dirac matrices, lower index 48
Dirac matrices, orthonormal system of, for Euclidean spaces 41
Dirac matrices, orthonormal system of, for pseudo-Euclidean spaces 42Ч44
Dirac matrices, upper index 48
Dirac's equation for hydrogen-like atoms 204Ч216
Dirac's equation for the electron 170Ч216
Dirac, Paul A.M. 41 170
Dirac, Paul A.M., introduction of Dirac matrices 41
Dirac, Paul A.M., prediction of positrons 181
Direct product 295
Direct sum 293Ч294
Dual vector space 51
Duality rotation 311
Eddington, Arthur S. 170 283 286
Eddington, Arthur S., his form of the Schwarzschild metric 283 286
Einstein, Albert 26 27 127
Einstein, Albert, field equations cast in form of a Yang Ч Mills field xv 149Ч154
Einstein, Albert, General Theory of Relativity 111
Einstein, Albert, Special Theory of Relativity 25Ч40
Electric dipole of a free electron 184
Electromagnetic-momentum tensor 143
Energy-momentum tensor 149
Euler Ч Lagrange equations for the motion of a planet according to Newton's theory 117Ч123
Euler Ч Lagrange equations for the motion of a planet according to the Schwarzschild metric 123Ч127
Euler Ч Lagrange equations for the rotating top 18
Exterior derivative d 130Ч137
Exterior product 55
Faraday 2-vector 138
Faraday tensor 138Ч141
Field strength tensor for a Yang Ч Mills field 144
Fine structure constant 205
Flanders, Harley 58 131 136
Fock Ч Ivanenko 2-vectors, applications of xivЧxv
Fock Ч Ivanenko 2-vectors, computation of curvature 2-forms 101Ч103
Fock Ч Ivanenko 2-vectors, computation of Schwarzschild metric 111Ч116
Fock Ч Ivanenko 2-vectors, definition and formula for 93Ч94
Fock Ч Ivanenko 2-vectors, history of introduction of 171
Fock, Vladimir A. xiv 93 171 178
Franz, Walter 170
Free charges and currents 141Ч142
Friedman metric 103Ч104 116
Galle, Johann Gottfried, discovery of Neptune 126
Gallilean transformation 26
Gauge potential for Yang Ч Mills field xv 144
Gauss's theorem 169
Gaussian curvature for more general surfaces 65
| Gaussian curvature of a sphere 62
Gaussian curvature, surfaces with negative curvature 66Ч67
Gaussian curvature, surfaces with zero curvature 65Ч67
General linear group 305
Generalized Kronecker delta symbol 54
Generalized Laguerre polynomials 210 214
Generalized Stoke's theorem 161Ч169
Generators of an algebra 295
Geodesic 60Ч61 81Ч82
Geodesic, triangle 61
Georgi, Howard 287
Glauber, Roy J. 170
Goldstein, Herbert 23
Gordon decomposition 173Ч175
Gordon, Morton M. 154
Gordon, Walter 173
Graham, Alexander 291
Guess and check method 116
Guggenheimer, Heinrich W. 131
Hamilton, William 7Ч8
Herlt, E. 264
Hestenes, David 57 311
Hodge star operator 136Ч137
Hydrogen atom, energy levels of, from Dirac's equation 209Ч211
Hydrogen atom, energy levels of, from Schroedinger's equation 212
Index free Clifford number 53 88
Index lowering operator 52
Index raising operator 52
Inertial mass 37
Internal current 174Ч175
Isotropic vector 76
Itzykson, Claude 179
Ivanenko, Dimitrii xiv 93 171
J, normalized pseudo-scalar 134Ч136
Jackson, John David 191
Jacobi identities 96
Johnson, David A. 154
Kaluza, Theodor 44
Kepler's first law 121
Kepler's second law 118
Kepler's third law 122Ч123
Kerr metric 217Ч249 272Ч286
Kerr, Roy P. 217
Kramer, D. 250 264
Kronecker delta symbol, generalized 54
Kronecker product 291 295
Kummer's differential equation 208
Kummer's function 208Ч211
Laguerre generalized polynomials 210Ч211 214Ч215
Laplacian operator in cylindrical coordinates 53
Laplacian operator in Euclidean coordinates 52
Laplacian operator in spherical coordinates 53
Leibniz property 86 89
Lense Ч Thirring line element 246Ч247
Lense, Von J. 246
Leverrier, Urbain Jean Joseph, precession of Mercury 127
Leverrier, Urbain Jean Joseph, prediction of Neptune 126
Light-like eigenvector of a Lorentz transformation 321Ч322
Light-like plane 322
Light-like vector 76 321Ч322
Lindquist, Richard W. 242
Lorentz contraction 32Ч34
Lorentz force 138 142
Lorentz transformation 26 308
Lorentz transformation, restricted 308
Lorentz, Hendrik 25Ч26
Lounesto, Pertti 294Ч295
Lower index Dirac matrices 48
Lune 61
MacCallum, M. 264
Maglich, Bogdan, his migma chamber 154Ч161
Magnetic dipole of a free electron 184
Magnus, Wilhelm 209 214Ч215
Margenau, Henry 237
Martin, Paul C. 170
Mass, inertial 37
Mass, rest 37
Maxwell's equations 137Ч144
Maxwell's equations and special relativity 25
Mercury, precession of 117Ч127
Metric tensor 47
Metric tensor, degenerate 104
Michelson, Albert A. 25
Migma chamber of Bogdan Maglich 154Ч161
Minkowski space 27Ч29
Misner, Charles W. 116
Mixed tensor 51
Mixed tensor, alignment of indices 51
Moment of inertia coefficients for spinning top 18Ч23
Morley, Edward W. 25
Murphy, George Moseley 237
n-dimensional orthonormal Euclidean system of Dirac matrices 41
Neptune, discovery of 126
Neutrino, prediction and discovery of 37
Newcomb, Simon, precession of Mercury 127
Non-singular metric 50 see
Normalized pseudo-scalar J 134Ч136
Notation for coordinate Dirac matrices 45
Notation for non-coordinate Dirac matrices 45
Null eigenvectors of a Lorentz transformation 322
Null plane 267
Null rotation 321
Nutation of a spinning top 22
Oberhettinger, Fritz 209 214Ч215
Oblate spherical coordinates 237Ч240
Orthochronous Lorentz transformation 256Ч257
Orthonormal system of Dirac matrices for Euclidean spaces 41
Orthonormal system of Dirac matrices for pseudo-Euclidean spaces 42Ч44
p-tangent vector 42
p-vector 42
Palatini action 150
Parallel transport 62Ч65 80Ч83
Pauli matrices 10
Pauli, Wolfgang, criticism of Dirac's antiparticle 181
Pauli, Wolfgang, postulation of neutrino 37
Penrose, Roger xiv 89 97 322
Petrov matrix 250Ч255
Petrov's canonical forms 250Ч263
Petrov's canonical forms, summary 263
Petrov, Aleksei Zinoveivich 250
phase velocity 184
Planetary motion, according to Newton's theory 117Ч123
Planetary motion, according to the Schwarzschild metric 123Ч127
Poincare lemma 133Ч134
Poincare lemma, converse of 133
Poincare, Henri, special relativity 26
Porteous, Ian R. 43 294 297
Position vector 45
Precession for rotating top, angle of 14
Precession for rotating top, rate of 22Ч23
Precession of the perihelion for Mercury 117Ч127
Principal null congruence 248
Principal null directions 266Ч277
Proca, Alexandre 170
Projection operators 313 323
Projection operators for Dirac's equation for electron 183
Proper time interval 36
Pseudo-Euclidean space 42Ч43
Pseudo-scalar 9
Pseudo-scalar, normalized 134Ч136
Pseudo-vector 8
Quaternions 7Ч8
Real Clifford algebra 42
Real Clifford number 42
Regular point 70
Reines, Frederick, discovery of neutrino 37
Rest mass 37
Restricted Lorentz transformation 308
Restricted Lorentz transformation, exponential representation of 314Ч323
Reverse of a Clifford number, complex 171
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 periodicity of rotation operator
periodicity of rotation operator