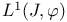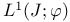|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gripenberg G., Londen S.O., Staffans O. — Volterra integral and functional equations |
|
|
 |
| Предметный указатель |
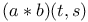 19[1.3.9] 226 228[9.2.3] 228[9.2.4] 243[9.5.3] 250[9.6.7] 19[1.3.9] 226 228[9.2.3] 228[9.2.4] 243[9.5.3] 250[9.6.7]
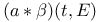 294[10.3.5] 294[10.3.5]
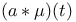 293[10.3.4] 293[10.3.4]
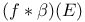 292[10.3.2] 292[10.3.2]
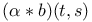 294[10.3.5] 294[10.3.5]
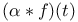 285[10.2.2] 287[10.2.3] 292[10.3.2] 285[10.2.2] 287[10.2.3] 292[10.3.2]
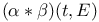 20[1.3.10] 287 287[10.2.3] 294[10.3.5] 20[1.3.10] 287 287[10.2.3] 294[10.3.5]
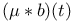 293[10.3.4] 293[10.3.4]
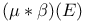 285[10.2.2] 287[10.2.3] 285[10.2.2] 287[10.2.3]
 496 496
![$adj[\nu]$](/math_tex/40c3129bb8a2d872eb300c59fd55e85882.gif) 124 135 124 135
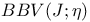 , , 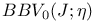 116 116
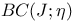 , , 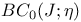 116 315[11.2.3] 316[11.2.4] 116 315[11.2.3] 316[11.2.4]
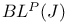 , , 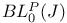 xviii 73 xviii 73
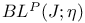 , , 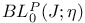 115 116 115 116
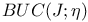 116 116
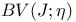 116 116
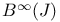 , , 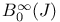 , , 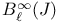 , , 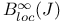 xviii xviii
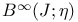 , , 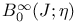 116 116
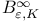 361 361
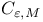 348 348
![$det[\nu]$](/math_tex/420168ffa7afc847e6ec4e4c5ad8227182.gif) 124 135 124 135
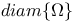 xxi 346 xxi 346
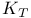 353 358[12.2.9] 353 358[12.2.9]
 -anti-accretive type see "Kernel Lp-anti-accretive -anti-accretive type see "Kernel Lp-anti-accretive
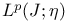 115 115
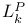 357 361 357 361
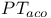 516[16.5.4] see anti-coercive 516[16.5.4] see anti-coercive
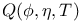 xxii xxii
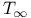 348 348
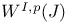 xix xix
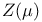 see "Kernel Fourier see "Kernel Fourier
![$[\nu,\phi]$](/math_tex/21d98b9c87009b74c0bbd0696f5e399182.gif) xxi xxi
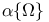 346 379 346 379
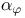 120[4.4.1] 120[4.4.1]
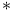 -product xxi see -product xxi see
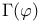 , , 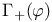 , , 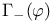 453[15.2.1] see set" 453[15.2.1] see set"
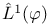 , locally in , locally in 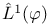 199[7.3.1] 199[7.3.2] 199[7.3.1] 199[7.3.2]
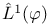 , locally in , locally in 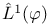 at at  199[7.3.1] 199[7.3.1]
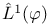 -smooth of order p 200[7.3.5] 200[7.3.7] -smooth of order p 200[7.3.5] 200[7.3.7]
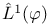 -zero of order p 200[7.3.6] 200[7.3.7] -zero of order p 200[7.3.6] 200[7.3.7]
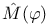 , locally in , locally in 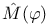 199[7.3.3] 200[7.3.4] 199[7.3.3] 200[7.3.4]
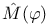 , locally in , locally in 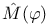 at at  199[7.3.3] 199[7.3.3]
 , , 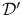 xix 527 527—530 xix 527 527—530
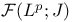 227[9.2.2] 227[9.2.2]
 227[9.2.2] see " 227[9.2.2] see "
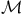 see "Kernel nonconvolution see "Kernel nonconvolution
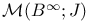 284[10.2.1] 284[10.2.1]
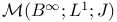 292[10.3.1] 292[10.3.1]
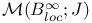 290[10.2.11] 290[10.2.11]
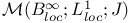 295[10.3.6] 295[10.3.6]
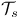 xvii xvii
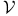 see "Kernel" see "Kernel"
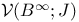 242[9.5.1] 242[9.5.1]
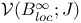 242[9.5.1] 242[9.5.1]
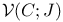 242[9.5.2] 242[9.5.2]
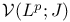 227[9.2.2] 227[9.2.2]
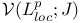 240[9.4.1] 240[9.4.1]
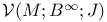 293[10.3.3] 293[10.3.3]
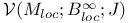 295[10.3.6] 295[10.3.6]
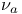 , , 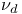 , , 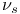 xxi 79 113 123 xxi 79 113 123
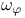 120[4.4.1] 120[4.4.1]
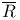 176 176
 -sequence 486 -sequence 486
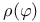 472[15.5.1] 473[15.5.3] 472[15.5.1] 473[15.5.3]
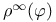 476[15.6.1] 476[15.6.1]
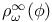 476[15.6.1] 476[15.6.1]
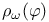 472[15.5.1] 472[15.5.2] 473[15.5.3] 474[15.5.6] 475[15.5.7] 475[15.5.8] 485 472[15.5.1] 472[15.5.2] 473[15.5.3] 474[15.5.6] 475[15.5.7] 475[15.5.8] 485
 -algebra 285 294 -algebra 285 294
 -finite measure space 90[3.4.1] 91 -finite measure space 90[3.4.1] 91
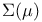 461[15.4.1] see of 461[15.4.1] see of
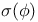 xx 462[15.4.4] 462 see of xx 462[15.4.4] 462 see of
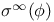 476[15.6.1] 476[15.6.2] 548[17.3.7] 476[15.6.1] 476[15.6.2] 548[17.3.7]
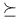 , , 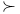 xxi xxi
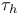 xx 63[2.7.1] 63[2.7.2] 63[2.7.3] 316 453[15.2.2] 492 xx 63[2.7.1] 63[2.7.2] 63[2.7.3] 316 453[15.2.2] 492
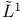 , locally in , locally in 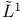 176[6.3.1] 177[6.3.2] 177[6.3.3] 179[6.3.5] 179[6.3.6] 183 185[6.6.1] 185[6.6.2] 185[6.6.3] 176[6.3.1] 177[6.3.2] 177[6.3.3] 179[6.3.5] 179[6.3.6] 183 185[6.6.1] 185[6.6.2] 185[6.6.3]
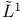 , locally in , locally in 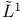 at at  176[6.3.1] 177[6.3.4] 179[6.3.5] 179[6.3.6] 185[6.6.1] 185[6.6.2] 176[6.3.1] 177[6.3.4] 179[6.3.5] 179[6.3.6] 185[6.6.1] 185[6.6.2]
Abel's equation 158
Absolute continuity 427[14.2.2] 442[14.4.1] 442[14.4.3] 443[14.4.5] 443[14.4.6]
Accretive operator 624
Adjoint, Banach space adjoint 213
Adjoint, equation 274
Adjoint, matrix see "Matrix adjoint"
Adjoint, semigroup see "Semigroup adjoint"
Admissible 278 338
Admissible, 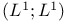 272[9.10.4] 272[9.10.4]
Admissible, 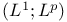 277[9.11.3] 277[9.11.3]
Admissible, 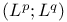 278 278
Admissible, 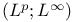 277[9.11.3] 277[9.11.3]
Admissible, 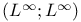 271 [9.10.2] 271 [9.10.2]
Aerofoil section 12[1.2.8]
Almost-periodic function 65 470[15.4.17] 471 472[15.4.19] 484-485
Almost-periodic function in the sense of Stephanov 65
Analytic 177[6.3.3] 177[6.3.4] see analytic"
Anti-coercive type 516[16.5.4] see anti-coercive
Anti-symmetric matrix 141[5.2.1] 493[16.2.3] 501[16.3.3]
Approximate, convolution identity 67[2.7.4] 528
Approximate, equation 404
Approximate, multiplicative identity 528
Arithmetic measure 511
Arzela — Ascoli theorem 68[2.7.5] 68(2.7.6]
Associative algebra 233[9.3.2] 233[9.3.4] 234[9.3.5] 239[9.3.17] 290[10.2.10]
Asymptotic, directional spectrum 476[15.6.1]
Asymptotic, spectral subspace 476[15.6.1]
Asymptotic, spectrum 476[15.6.1] 476[15.6.2] 548[17.3.7]
Asymptotic, stability 426
Asymptotically, almost-periodic function 39 65
Asymptotically, drifting periodic function 459[15.3.4] 459[15.3.5] 476[15.6.2] 483
Asymptotically, periodic function 39 65
Asymptotically, slowly varying function 458[15.3.2] 458[15.3.3] 476[15.6.2] 480[15.8.1] 483-484
Autonomous, equation 316
Autonomous, operator 454[15.2.5] 454[15.2.7] 456[15.2.9] 456[15.2.11] 480[15.8.1] 624 see invariant
Banach algebra 228
Banach algebra of  -functions 275-276 -functions 275-276
Banach algebra of convolution measure kernels 113[4.1.3] 119[4.3.4] 136[4.6.2]
Banach algebra of nonconvolution kernels 19[1.3.9] 228[9.2.4] 243[9.5.3] 247[9.6.2] 249[9.6.5] 250[9.6.7] 251[9.6.9] 252[9.6.12] 256[9.7.5] 275[9.11.1] 275[9.11.2]
Banach algebra of nonconvolution measure kernels 20[1.3.10] 287[10.2.3]
Banach module 228 228[9.2.4] 247[9.6.2] 249[9.6.5] 251[9.6.9] 252[9.6.12] 287[10.2.3]
BBV(J), 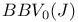 xviii 73 xviii 73
Bernstein function 161
Bernstein's theorem 17[1.3.5] 143(5.2.5]
beta function 415[13.6.3]
Bochner's theorem 26[1.3.16] 498[16.2.7] 499 506 595—596
Boundary of the spectrum 467[15.4.13] 467[15.4.14]
Boundedness principle 427[14.2.2] 428[14.2.3] 429[14.2.4] 429[14.2.5] 430[14.2.6] 431[14.2.8]
Caratheodory conditions 355 356
Cauchy's theorem 153
Causal 345 348 348[12.2.1] 360[12.3.1] 362[12.4.1] 363[12.4.2] 533
Characteristic, equation 137 193[7.2.2] 219
Characteristic, exponent 192-196 193[7.2.2] 198 200-202 219
coercivity constant 27[1.3.16] 516[16.5.4] 516[16.5.5] 516[16.5.6] 517[16.5.7] 519 531
Compact see "Equicontinuity"
Compact in 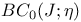 315[11.2.3] 316[11.2.4] 315[11.2.3] 316[11.2.4]
Compact in  357[12.2.8] 365[12.4.4] 365 373 357[12.2.8] 365[12.4.4] 365 373
Compact open topology see "Uniform convergence on compact subsets"
Compact, mapping 40 243[9.5.3] 255 256[9.7.5] 314[11.2.2] 632
Compact, mapping from 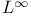 to to  367[12.4.5] 367[12.4.5]
Compact, mapping from  to to  253[9.7.1] 254[9.7.3] 253[9.7.1] 254[9.7.3]
Compact, mapping from  to to  253 254[9.7.2] 255[9.7.4] 279 368[12.4.6] 253 254[9.7.2] 255[9.7.4] 279 368[12.4.6]
Compact, mapping, convolution 40[2.2.5]
Compact, mapping, weakly compact 254
Compact, measure of noncompactness 346 379
Compact, set of solutions 404(13.4.4]
Compact, weak 156
Comparison, equation 257[9.8.2] 298[10.3.10] 359
Comparison, result 344 345[12.1.2] 353[12.2.4] 353 358 406[13.4.5] 406[13.4.7] 409[13.4.10] 410[13.5.2] 412[13.5.6]
Completely monotone function 142[5.2.3] 143[5.2.4] 143[5.2.5] 147[5.2.8] see completely
Completely monotone, kernel 17[1.3.5] see completely
Completely monotone, Laplace transform of a completely monotone function 144[5.2.6] 147[5.2.7]
Completely monotone, resolvent see "Resolvent completely
| Cone 403[13.4.1] 492[16.2.2] 625[20.4.7] 625[20.4.8] 626[20.4.10] 627[20.4.12]
Cone, solution in a cone 627[20.4.12] see maximal"
Continuation 343 see noncontinuable"
Continuous dependence see "Differential resolvent continuous "Resolvent continuous "Resolvent measure continuous "Solution continuous
Contraction mapping principle 314[11.2.1]
control systems 8[1.2.4]
Convex see "Function convex" "Kernel convex"
Convolution see "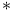 -product" -product"
Convolution, 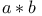 of functions 36 38[2.2.1] of functions 36 38[2.2.1]
Convolution, 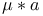 of a measure and a function 77 79[3.2.1] of a measure and a function 77 79[3.2.1]
Convolution, 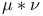 of measures 112[4.1.1] of measures 112[4.1.1]
Convolution, 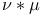 of distributions 529 of distributions 529
Convolution, 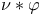 of a distribution and a test function 496 of a distribution and a test function 496
Convolution, compact mapping in  40[2.2.5] 40[2.2.5]
Convolution, derivative of a convolution 99[3.7.1] 100[3.7.2] 100[3.7.3] 101
Convolution, operator mapping 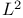 into into 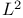 332[11.6.1] 332[11.6.1]
Convolution, properties 39[2.2.2] 40[2.2.3] 40[2.2.4] 63[2.7.2] 67[2.7.4] 96[3.6.1] 98[3.6.2] 113[4.1.2] 113[4.1.4] 119[4.3.4] 119[4.3.5] 133[4.5.1] 465[15.4.11]
Cosmic ray transport 4[1.2.1]
Critical line 18[1.3.7] 198 203
Cross section 353 358(12.2.9]
Delay equation 20[1.3.10] 283 345
Difference equation 16[1.3.4] 137
Differential resolvent 15[1.3.3] 77 81[3.3.2]
Differential resolvent in 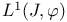 130[4.4.13] 130[4.4.14] 130[4.4.13] 130[4.4.14]
Differential resolvent in 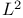 88[3.3.13] 334 88[3.3.13] 334
Differential resolvent in a weighted space 130[4.4.13] 130[4.4.14] 130(4.4.15] 131[4.4.16] 131
Differential resolvent of a completely monotone kernel 17[1.3.5] 150[5.4.1]
Differential resolvent of a kernel of positive type 604[19.4.1] 605[19.4.2] 606[19.4.3] 609[19.4.6]
Differential resolvent,  -remainder 192 [7.2.1] 200[7.3.7] -remainder 192 [7.2.1] 200[7.3.7]
Differential resolvent, bounded 445 [14.5.2]
Differential resolvent, continuous dependence 82[3.3.4]
Differential resolvent, derivative in 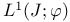 130[4.4.13] 130[4.4.14] 130[4.4.13] 130[4.4.14]
Differential resolvent, equation 15[1.3.3] 21[1.3.10] 77 81[3.3.1] 295
Differential resolvent, exponential decay 150[5.4.1]
Differential resolvent, exponentially growing 192[7.2.1]
Differential resolvent, integrable derivative 83[3.3.5]
Differential resolvent, integrable derivative, whole line 83[3.3.7]
Differential resolvent, integrate 83[3.3.5] 85[3.3.9] 89[3.3.16] 89[3.3.17] 150[5.4.1] 181[6.4.3] 181[6.4.4]
Differential resolvent, integrate, whole line 83[3.3.7] 86[3.3.10]
Differential resolvent, jump discontinuity 83[3.3.7]
Differential resolvent, maps 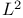 into into 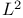 89[3.3.14] 89[3.3.14]
Differential resolvent, nonconvolution 21[1.3.10] 295 296[10.3.7] 296[10.3.8] 299[10.4.1]
Differential resolvent, of a convex kernel 184 187
Differential resolvent, parameter-dependence 184 187
Differential resolvent, periodic 88(3.3.12]
Differential resolvent, polynomially growing 200[7.3.7]
Differential resolvent, real-valued 81
Differential resolvent, type  300[10.4.3] 302[10.4.5] 446[14.5.6] 300[10.4.3] 302[10.4.5] 446[14.5.6]
Differential resolvent, type BC 301[10.4.4] 303[10.4.6]
Differential resolvent, type BUC 299[10.4.2]
Differential resolvent, unbounded 192[7.2.1] 200[7.3.7]
Differential resolvent, unique 81[3.3.1] 83[3.3.7] 130[4.4.14] 296[10.3.7]
Differential resolvent, used in a nonlinear equation 603
Differential resolvent, used in a perturbed linear equation 313 324 334
Differential resolvent, variation of constants formula 299[10.4.1]
Differential resolvent, whole line 78 83[3.3.7] 84[3.3.8] 86[3.3.10] 130[4.4.14] 130[4.4.15] 131[4.4.17] 193[7.2.1]
Differential resolvent, zero at infinity 89[3.3.17]
Differential-delay equation 2 24[1.3.14] 76 105 283 427 434 447[14.5.9]
Directional spectrum 472[15.5.1] 473[15.5.3]
distribution 527
Distribution, bounded 531
Distribution, convolution of two distributions 529
Distribution, derivative of a distribution 99[3.7.1] 100 103 528
Distribution, Fourier transform of a convolution 528
Distribution, Fourier transform of a distribution 103 495 521[16.6.2] 524[16.6.5] 528 529[16.8.1]
Distribution, integrable 183
Distribution, Laplace transform of a distribution 496 529 529(16.8.1]
Distribution, Plancherel's theorem for distributions 496 522
Distribution, positive type 533
Distribution, support of a distribution 528
Distribution, tempered 26[1.3.16] 495[16.2.5] 495 497[16.2.6] 514[16.5.2] 521[16.6.2] 524[16.6.5] 527
Duality mapping 216[8.3.5]
Eigenfunction 219-220
Eigenvalue 219 see
Epidemiology 6[1.2.3] 449
equation see "Fredholm" "Functional" "Solution "Solution "Volterra"
Equicontinuity 315[11.2.3] 349 353[12.2.3] 356[12.2.7] 392[13.2.2]
Existence of solution see "solution of a nonlinear equation exists"
Exponential polynomial 192
Exponentially growing solution see "Solution of a linear equation exponentially
Extended semigroup see "Semigroup extended"
Feedback 2—3 8[1.2.4]
Fejer kernel 51
Finite delay 203 207
Finitely generated limit set see "Limit set finitely
First kind see "Volterra equation of the first kind"
Fixed point theorem 22[1.3.11] 22[1.3.12] 314[11.2.1] 314[11.2.2] 346[12.1.3] see
Forcing function 35 225
Forcing function semigroup see "Semigroup forcing
Fourier coefficient 57
Fourier transform 41 50
Fourier transform in 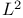 530[16.8.2] 530[16.8.2]
Fourier transform of a convex function 170[6.2.2] 186
Fourier transform of a distribution 495 529[16.8.1] see Fourier
Fourier transform of a kernel of anti-coercive type 516[16.5.6]
Fourier transform of a kernel of positive type 494[16.2.4] 497[16.2.6]
Fourier transform of a kernel of strict positive type 510[16.4.5]
Fourier transform of a kernel of strong positive type 507-508
Fourier transform of a nonnegative, nonincreasing function 173[6.2.3]
Fourier transform of an  -function 177[6.3.2] 464[15.4.8] -function 177[6.3.2] 464[15.4.8]
Fourier transform of bounded variation 467[15.4.15] 548[17.3.8]
Fourier transform, absolutely continuous 182[6.5.1]
Fourier transform, Hoelder-continuous 467[15.4.15] 548[17.3.8]
Fourier transform, inversion formula 183 499
Fourier zero-set see "Kernel Fourier
Frechet-derivative 397
Fredholm, integral equation 3 48[2.4.6]
Fredholm, integrodifferential equation 15[1.3.3] 86[3.3.10]
Fredholm, kernel 14[1.3.2] 15[1.3.3] 16[1.3.4] 227[9.2.1]
Fredholm, resolvent 232[9.3.1] see whole "Resolvent whole
Fubini's theorem 90(3.4.1] 91(3.4.2] 91(3.4.3]
Function see "Kernel"
Function, almost-periodic 65 470[15.4.17] 471 472[15.4.19] 484-485
Function, anti-coercive type 516[16.5.4]
Function, asymptotically almost-periodic 39 65
Function, asymptotically drifting periodic 459[15.3.4] 459[15.3.5] 476[15.6.2] 483
Function, asymptotically periodic 39 65
Function, asymptotically slowly varying 458[15.3.2] 458[15.3.3] 476[15.6.2] 480[15.8.1] 483—484
Function, completely monotone 142[5.2.3] 143[5.2.4] 143[5.2.5] 147[5.2.8]
Function, convex 500[16.3.1] 508[16.4.3]
Function, locally in 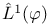 see see 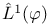
Function, locally in 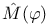 see see 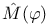
Function, locally in 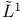 see " see "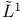 " "
Function, periodic 459(15.3.5] 460(15.3.7] 470(15.4.17]
Function, positive definite 426
Function, positive type 492(16.2.1]
Function, strict positive type 510(16.4.4]
Function, strong positive type 507(16.4.1]
Function, submultiplicative 118(4.3.2] 120[4.4.1]
Function, total variation 92(3.5.1]
Functional, differential equation 23[1.3.12] 77 107 203 345 360[12.3.1] 378 438 456—457 see
Functional, equation 22[1.3.12] 345 347 352[12.2.2] 353[12.2.3] 361 455
Fundamental solution 77 301
Gel'fand's theorem 121[4.4.2] 125[4.4.3] 125[4.4.4] 127[4.4.7] 127[4.4.8]
Gradient 539 see gradient"
Green's function 73 108 see whole "Resolvent whole
Gronwall's inequality 257[9.8.2] 291[10.2.15] 298[10.3.10] 306—307
Hammerstein operator 343
Hardy space 151 182 599
Hardy — Littlewood inequality 183
Hausdorff maximality principle 343
Heat equation 1
Heat flow 12[1.2.9]
Hoelder's inequality, matrix version 525 527
Homomorphism 121 126[4.4.6] 136[4.6.2]
Hyperstability 535
Ideal 126[4.4.6] 469 484[15.10.2]
identities 574[18.4.1] 576[18.4.4] 581[18.5.1] 583[18.5.4] 639[20.5.1] 643
Imaginary part see "Matrix imaginary
Initial function correction 208 215
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



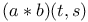
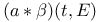
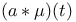
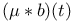
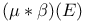

![$adj[\nu]$](/math_tex/40c3129bb8a2d872eb300c59fd55e85882.gif)
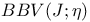 ,
, 
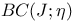 ,
, 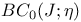
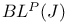 ,
, 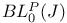
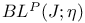 ,
, 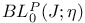
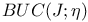
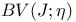
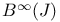 ,
, 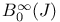 ,
, 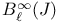 ,
, 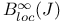
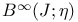 ,
, 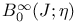
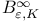
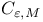
![$det[\nu]$](/math_tex/420168ffa7afc847e6ec4e4c5ad8227182.gif)
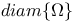
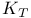
 -anti-accretive type
-anti-accretive type 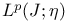
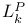
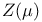
![$[\nu,\phi]$](/math_tex/21d98b9c87009b74c0bbd0696f5e399182.gif)
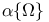
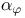
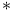 -product
-product 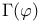 ,
, 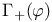 ,
, 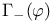
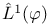 , locally in
, locally in 
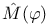 , locally in
, locally in  ,
, 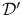
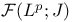

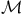
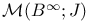
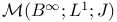
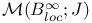
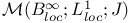
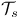
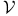
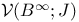
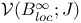
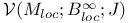
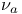 ,
, 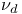 ,
, 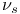
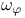
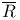
 -sequence
-sequence 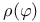
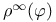
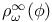
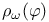
 -algebra
-algebra 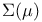
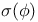
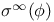
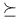 ,
, 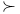
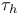
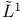 , locally in
, locally in 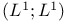
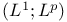
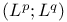
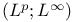
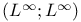
 -functions
-functions 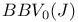
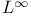 to
to 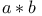 of functions
of functions 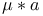 of a measure and a function
of a measure and a function 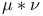 of measures
of measures 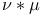 of distributions
of distributions 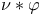 of a distribution and a test function
of a distribution and a test function 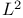 into
into