|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Chari V., Pressley A. Ч A Guide to Quantum Groups |
|
|
 |
| ѕредметный указатель |
Lie bialgebra, triangular 54
Lie Ч Poisson structure 19Ч20 21
Link invariants 167Ч168 497
Link invariants from R-matrices 504Ч510
Link invariants from vertex models 510Ч517
Linking number 500Ч501
links 167
Links, equivalent 496
Links, oriented 496
Links, skein related 497
Local algebra 158
Loop representation 542
Lusztig's canonical basis, algebraic construction 486Ч488
Lusztig's canonical basis, positivity property 487
Lusztig's canonical basis, topological construction 488Ч490
Lusztig's conjectures 359Ч361
Manin triples 26Ч32
Manin triples, infinite-dimensional 28
Markov equivalence 502
Markov moves 502
Markov trace 506
Matched pair 48
Matrix elements 106 116 430
Matrix elements and little q-Jacobi polynomials 466
Matrix elements and little q-Legendre polynomials 467
Matrix elements and q-Bessel functions 470Ч473
Modified classical Yang Ч Baxter equation (MCYBE) 55
Modified classical Yang Ч Baxter equivalent solutions 80
Modular Hopf algebra 517Ч521
Module 108
Module algebra 109
Module coalgebra 109
monodromy 540
Monodromy theorem 549Ч550
Monoidal functor 138Ч139
Monomorphism 137
Non-linear Schroedinger equation 422
Non-restricted integral form 289
Non-restricted specialization 288Ч296
Non-restricted specialization and conjugacy classes 295Ч296 342Ч343 347
Non-restricted specialization and R-matrices 348Ч351
Non-restricted specialization automorphisms 293Ч295
Non-restricted specialization centre 290Ч292
Non-restricted specialization defining relations 289
Non-restricted specialization relation with 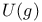 290 290
Non-restricted specialization representations 339Ч348
Opposite algebra 101
Opposite coalgebra 103
Orbit principle 180 439 442
Ore condition 232 244
Pairing of Hopf algebras 114Ч115 224Ч226 461
Partition function 247 249 510
Pentagon axiom 139
Perverse sheaves 490
Peter-Weyl theorem 451
Pluecker relations 448
Poincare Ч Birkhoff-Witt 199Ч200 260 282Ч283 291 298 302 382 394 433
Poisson action 36Ч37
Poisson algebra 43 177
Poisson algebra deformation 44
Poisson bivector 17
Poisson bracket 16Ч17
Poisson homogeneous space 22Ч24
Poisson homogeneous space, Hopf fibration as 23Ч24
Poisson homogeneous space, symplectic leaves of 38
Poisson manifold 16Ч21
Poisson manifold, complex 20Ч21
Poisson map 18
Poisson structure 16Ч17
Poisson structure, compatible 41
Poisson submanifold 18
Poisson Ч Hopf algebra 177Ч178
Poisson Ч Lie group 21Ч24 292Ч293 296
Poisson Ч Lie group, coboundary 59Ч68
Poisson Ч Lie group, compact 35Ч36
Poisson Ч Lie group, complex 26
Poisson Ч Lie group, double 34 37Ч38 43
Poisson Ч Lie group, dual 33Ч34 37Ч38 296
Poisson Ч Lie group, factorizable 67
Poisson Ч Lie group, homomorphism 21
Poisson Ч Lie group, Lie bialgebra of 26
Poisson Ч Lie group, subgroup 22
Pontryagin duality 135
Pontryagin product 108
Primitive element 107
Primitive ideal 454
Primitive vector 314 354 383
Principal alcove 362
Pro-finite fundamental group 557
PRODUCT 18
Product, rank of 19 22
Product, second Adler Ч Gel'fand Ч Dickii 32
Product, symplectic 18
Product, trivial 18
Product, twisted 42Ч43
Pseudo-differential operators 31Ч32
Pseudo-highest weight 396
Pseudo-universal R-matrix 419 423
Pure braid group 144 153 538
Pure sphere braid group 538
q-Bessel function 470
q-Bessel function, addition formula 471
q-Bessel function, Hansel Ч Lommel orthogonality relation 471
q-binomial coefficient 200 209 301
q-derivative 464
Q-exponential 273
q-factorial 200
q-Hahn polynomial 467
Q-hypergeometric series 430 465 561
q-integral see Jackson integral
q-Jacobi polynomial, big 468Ч469
q-Jacobi polynomial, little 466Ч467
q-Legendre polynomial 467
q-number 200
q-spherical function 468Ч469
QF algebra 176 216Ч227 234Ч240 430
QF algebra *-representations 433 437Ч438 441Ч442
QF algebra *-structure 431Ч432
QF algebra admits a faithful representation 438Ч439
QF algebra and classical function algebra 306 443Ч444
QF algebra at roots of unity 301 442Ч445
QF algebra centre 219
QF algebra, differential calculus on 240Ч246
QF algebra, highest weight representations 227 433Ч438 441Ч442
QF algebra, multiparameter 238Ч240
QF algebra, PBW factorization 433
QF algebra, rational form 280Ч281
QF algebra, twisted 439Ч442
QFSH algebra 190 267Ч268
Quantization of co-Poisson Ч Hopf algebras 180
Quantization of Lie bialgebras 180Ч189
Quantization of Poisson Ч Hopf algebras 179
Quantization of Poisson Ч Lie groups 179
Quantization of quasi-Hopf algebras 537
Quantization, deformation 46Ч47
Quantization, homogeneous 375Ч376
Quantization, Moyal 46Ч47 183Ч187
Quantization, multiparameter 212Ч213 238Ч240
Quantization, non-standard 206Ч207
Quantization, R-matrix 187 222Ч223 228Ч234
Quantization, standard 195 208 234Ч235
Quantization, Weyl 44Ч45
Quantized algebra of continuous functions 451Ч452
Quantized algebra of continuous functions, vanishing at infinity 461Ч462
Quantized function algebra see QF algebra
Quantum 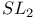 192Ч206 216Ч227 192Ч206 216Ч227
Quantum 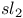 and little g-Jacobi polynomials 466Ч467 and little g-Jacobi polynomials 466Ч467
Quantum 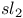 , algebra structure 196 , algebra structure 196
Quantum 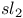 , automorphisms 309 , automorphisms 309
Quantum 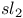 , basis 199 220Ч222 226 , basis 199 220Ч222 226
| Quantum 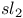 , centre 285 291Ч292 321Ч323 , centre 285 291Ч292 321Ч323
Quantum 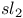 , matrix elements 466 , matrix elements 466
Quantum 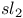 , quantum Weyl group 262Ч263 , quantum Weyl group 262Ч263
Quantum 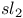 , quasitriangular structure 201Ч203 , quasitriangular structure 201Ч203
Quantum 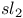 , real forms 309Ч311 , real forms 309Ч311
Quantum 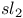 , representations 203Ч206 330Ч331 343Ч344 , representations 203Ч206 330Ч331 343Ч344
Quantum 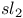 , tilting modules 364Ч366 , tilting modules 364Ч366
Quantum 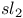 , universal R-matrix 201 263Ч265 , universal R-matrix 201 263Ч265
Quantum 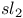 , Weyl modules 355Ч356 , Weyl modules 355Ч356
Quantum affine algebra 392Ч394
Quantum affine algebra, PBW basis 394
Quantum affine algebra, pseudotriangular structure 403 423Ч425
Quantum Casimir element 196 285 291Ч292 323
Quantum Clebsch Ч Gordan coefficient 205 467
Quantum coadjoint action 293Ч296
Quantum coadjoint action and conjugacy classes 295Ч296
Quantum coordinate ring see QF algebra
Quantum determinant 219 220 231Ч233 236
Quantum dimension 122Ч123 126 365Ч366 371
Quantum double 127Ч129 132
Quantum euclidean group 459Ч462 469Ч470
Quantum euclidean group representations 462Ч463
Quantum euclidean group, automorphisms 463
Quantum euclidean group, Haar integral 463Ч465
Quantum field theory 157Ч160
Quantum flag manifolds 447Ч448
Quantum G-space 445Ч447
Quantum Kac Ч Moody algebras 207Ч213
Quantum Kac Ч Moody algebras, automorphisms 309
Quantum Kac Ч Moody algebras, centre 212 284Ч285 290Ч293 321Ч324
Quantum Kac Ч Moody algebras, geometric realization 285Ч288 308Ч309
Quantum Kac Ч Moody algebras, real forms 309Ч311
Quantum Kac Ч Moody algebras, representations 313Ч331
Quantum loop algebras 396
Quantum loop algebras, relation with Yangians 403
Quantum loop algebras, representations 394Ч403
Quantum orthogonal group 236Ч238
Quantum plane 217Ч218 228 240Ч241
Quantum projective space 451
Quantum R-matrix 133 205 276Ч277
Quantum R-matrix, elliptic 427
Quantum R-matrix, Frobenius 231
Quantum R-matrix, Hecke 232
Quantum R-matrix, rational 380 419Ч423
Quantum R-matrix, singularities 425
Quantum R-matrix, strange 230
Quantum R-matrix, trigonometric 424
Quantum Schubert variety 448
Quantum Schur orthogonality relations 457Ч458
Quantum Serre relation 209
Quantum special linear group 235Ч236
Quantum spheres 448Ч451 467Ч469
Quantum symplectic group 236Ч238
Quantum torus 442
Quantum trace 122Ч123 126Ч127 365Ч366 370
Quantum Weyl group 262Ч266 439
Quantum Weyl group and central elements 265
Quantum Weyl group and universal R-matrix 263Ч265
Quantum Weyl group for quantum affine algebras 424
Quantum Yang Ч Baxter equation (QYBE) 67 124Ч125 187 203 229 250
Quantum Yang Ч Baxter equation (QYBE) and braid groups 504Ч505
Quantum Yang Ч Baxter equation (QYBE) and intertwiners 348Ч351
Quantum Yang Ч Baxter equation (QYBE) with spectral parameters 250 348Ч351 380 419Ч425 511
Quantum Yang Ч Baxter equation (QYBE), space of solutions of 233Ч234
Quasi-bialgebra 529
Quasi-bialgebra, quasitriangular 531
Quasi-bialgebra, triangular 531
Quasi-Frobenius Lie algebra 84
Quasi-Hopf algebra 130Ч131 529
Quasi-Hopf algebra, quasitriangular 531
Quasi-Hopf algebra, triangular 531
Quasi-Hopf QUE algebra 534Ч537
Quasi-Hopf QUE algebra, quasitriangular 536
Quasi-Lie bialgebra 536
Quasi-modular Hopf algebra 521
Quasi-Poisson Ч Lie group 48
Quasi-quantum Yang Ч Baxter equation 531
QUE algebra 176 187Ч192
QUE algebra, coboundary 188
QUE algebra, cocommutative 187Ч188
QUE algebra, quasitriangular 188
QUE algebra, rational form 280Ч281
QUE algebra, triangular 188
QUE double 190 266Ч267 270
QUE dual 190 267 268Ч270
quiver 307 488Ч490
Rational form 280Ч281
Rational form and R-matrices 327Ч329
Rational form, adjoint 281
Rational form, simply-connected 281
Real form 117Ч119
Real form, compact 431
Real form, equivalent 117
Reconstruction theorem 147Ч149
Reduced decomposition 565
Reduced decomposition, adapted 488
Regular dominant weight 433
Regular isotopy 500 512
Reidemeister moves 496Ч497
Representation and symplectic leaves 180 439 442 454
Representation, adjoint 110
Representation, characters 315
Representation, completely reducible 391
Representation, corresponding to a Schubert cell 435 441 448
Representation, cyclic 344Ч348
Representation, dual 110Ч111
Representation, faithful 438Ч439
Representation, highest weight 314 324 433
Representation, integrable 314 492 556 566
Representation, physical 158
Representation, pseudo-highest weight 396
Representation, regular 110
Representation, restricted 359
Representation, tame 415
Representation, tensor products 110
Representation, trivial 110
Representation, type 314 394 401
Representation, unitarizable 433
Representation, unitary 118 329Ч331 433
Representative functions 106 116
Restricted enveloping algebra 304 360
Restricted integral form 296Ч297
Restricted integral form of a representation 316
Restricted integral form, basis 298
Restricted integral form, generators and relations 299Ч300
Restricted representation 359
Restricted specialization 300
Restricted specialization and affine Lie algebras 360Ч361
Restricted specialization, centre 300
Restricted specialization, representations 351Ч361
Ribbon Hopf algebra 125Ч127 133 161 276 517
Ribbon Hopf algebra, central elements 168Ч169
Ribbon tangle 146Ч147 502
Ribbon tangle closure 164Ч165
Ribbon tangle, coloured 147
Ribbon tangle, directed 146Ч147
Ribbon tangle, isotopy invariants 161Ч166
Right dual 111 122
Rigidity theorems 176Ч177 212
Robinson Ч Schensted correspondence 478
Root 563
Root space 564
Root vector 259 282 565
Rotation number 501
Schouten bracket 17
Schubert cell 41 435 441 448
Segment 402
Short exact sequence 137
Simple object 137
Simple reflection 564
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



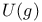
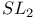
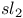 and little g-Jacobi polynomials
and little g-Jacobi polynomials