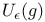|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Chari V., Pressley A. Ч A Guide to Quantum Groups |
|
|
 |
| ѕредметный указатель |
*-homomorphism 117
*-representation 433 437Ч439 441Ч442
3-manifold invariants 522Ч525
Absolute Galois group 557Ч560
Admissible 80 92 482
Affiliated element 462
Affine Hecke algebra 403
Affine Hecke algebra, relation with p-adic groups 404
Affine Hecke algebra, representations 405Ч408 410Ч413
Affine Lie algebra 58 541Ч543 550Ч556 565Ч566
Alexander polynomial 498 500
Algebra 101Ч102
Algebra, deformation 43
Algebra, opposite 101
Ambient isotopy 496 514
Angle 1-form 501
Antipode 103 529
Antipode, square of 190Ч192
arrow 482
Associativity constraint 139
Baker Ч Campbell Ч Hausdorff formula 46 182 185Ч186
Big cell 294
Birkhoff factorization theorem 96
Birman Ч Murakami Ч Wenzl algebra 334 526
Boltzmann weight 247 351 510
BOND 246
Braid 142Ч144
Braid closure 501
Braid group 143Ч144 153 256
Braid group and configuration spaces 538
Braid group, action 257 282 336
Brauer Ч Frobenius Ч Schur duality see Frobenius Ч Schur duality
Bruhat decomposition 39 41
Bruhat ordering 360 405 565
Burau representation 505
C* -completion 451Ч452
C* -completion, type of 454
Capelli identity 426
Cartan matrix 562
Cartan matrix, extended 565Ч566
Casimir element 196 275Ч276
Category, abelian 136Ч137 307
Category, additive 136Ч137
Category, balanced 154
Category, braided monoidal 153
Category, essentially small 148
Category, k-linear 137
Category, monoidal 138Ч147 530
Category, quasitensor 152Ч153 329 359 370 531 555 559Ч560
Category, rigid 139Ч140 530 555
Category, semisimple 137 391 556
Category, small 148
Category, strict 139
Category, tensor 149Ч152 531
Central character 290 315 340
Central elements 122 124 168Ч169 284 321Ч323
CHARACTER 317 325Ч326 353Ч354 361 363
Characteristic p 296 304Ч306 358Ч361 555Ч556
Classical limit of a QF algebra 179
Classical limit of a quasi-Hopf QUE algebra 536Ч537
Classical limit of a QUE algebra 180Ч182
Classical r-matrix 54 181Ч182 183Ч184
Classical r-matrix and 2-cocycles 62Ч63
Classical r-matrix and integrable systems 71Ч77
Classical r-matrix, non-degenerate 62 87
Classical Yang Ч Baxter equation (CYBE) 54 125 182 187
Classical Yang Ч Baxter equation (CYBE) and Lie bialgebras 51
Classical Yang Ч Baxter equation (CYBE) with spectral parameters 87
Classical Yang Ч Baxter equation (CYBE), class of solution of 96
Classical Yang Ч Baxter equation (CYBE), equivalent solutions of 80 84 88
Classical Yang Ч Baxter equation (CYBE), modified 55
Classical Yang Ч Baxter equation (CYBE), solutions of 80Ч98
Clebsch Ч Gordan decomposition 204 326
Co-Jacobi identity 178
Co-Leibniz identity 178
Co-Poisson algebra 178
Co-Poisson Hopf algebra 178
Coadjoint orbits 20 40Ч41
Coalgebra 102Ч103
Coassociativity 102
Coassociator 529
Coboundary 51 84 174
Cochain 173
Cocommutator 25 535
Cocycle 25 62 174 533
Cohomology of Hopf algebras 173Ч177
Cohomology of Hopf algebras, rigidity theorems for 176Ч177 212
Cokernel 137
Comodule 108
Comodule algebra 109
Comodule coalgebra 109
Compact matrix pseudogroup see compact matrix quantum group
Compact matrix quantum group 453Ч454
Compact matrix quantum group, Haar integral 454Ч458
Complete integrability 68Ч69
Complete reducibility 318Ч319 324Ч325
Comultiplication 102
Configuration spaces 537Ч538 558
Conformal field theory 159 371Ч372
Conformal field theory, orbifold 534
Conformal weight 542
Conserved quantities 69
Conserved quantities in involution 69
Continued fraction 331
Continuous series 331
Contravariant form 320
Convolution product 104
Core 146
Corepresentation 110 141
Corepresentation, regular 110
Corepresentation, unitary 118
Coxeter automorphism 91
Coxeter element 489 565
Coxeter number 92 489 565
Crystal basis 478Ч486
Crystal basis, global 480Ч486
Crystal graph 484
De Rham complex of quantum 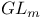 244Ч245 244Ч245
De Rham complex of quantum 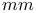 matrices 242Ч243 matrices 242Ч243
De Rham complex of quantum plane 240Ч241
De Rham complex, homology of 243Ч244
Deformation of algebras 43
Deformation of bialgebras 171
Deformation of Hopf algebras 171
Deformation of Poisson algebras 44
Deformation, (mod 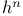 ) 172 ) 172
Deformation, quantization 44 46Ч47
Degenerate affine Hecke algebra 405
Derivation 190Ч192
Determinant formula 321 327
Diagonal module 342
Diagram automorphism 309
Differential graded algebra 242
Direct sum 136
Directed tangle 145
Discrete series 330
Discriminant 340Ч341
Dressing action 37Ч38
Dressing action and symplectic leaves 38Ч41
Dressing transformation 37Ч38
Dual basis lemma 141
Dual Coxeter number 564
Dual object 139
Dual object functor 140
Dynkin diagram 92 562
Dynkin graph 307
Eight vertex model 253
Elliptic solutions of the CYBE 90Ч91
Elliptic solutions of the QYBE 427
Enhanced quantum Yang Ч Baxter operator 506
| Epimorphism 137
Equivalence of deformations 171
Equivalence of solutions of the CYBE 80 84 8?
Euclidean group 459
Evaluation homomorphism for affine Hecke algebras 407
Evaluation homomorphism for quantum loop algebras 399Ч401
Evaluation homomorphism for Yangians 386Ч387
Evaluation representations of affine Hecke algebras 407
Evaluation representations of quantum loop algebras 399Ч403
Evaluation representations of Yangians 386Ч391
Exterior algebra 107Ч108
Fateev Ч Zamolodchikov model 351
Fibonacci sequence 331
Framing 502
Frobenius Lie algebra 84
Frobenius map 305Ч306 357 359
Frobenius Ч Schur duality for 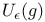 334Ч335 408Ч410 334Ч335 408Ч410
Frobenius Ч Schur duality for quantum affine algebras 410Ч413
Frobenius Ч Schur duality for Yangians 413Ч414
Frobenius Ч Schur duality, classical 332
Fuchsian differential equations 544
Functor, exact 148
Functor, faithful 148
Functor, monoidal 138Ч139
Functor, tensor 150
Fundamental reflection see simple reflection
Fundamental representations of quantum loop algebras 399
Fundamental representations of Yangians 384 387Ч388
Fundamental weight 564
Fusion matrices 155
Fusion ring 155 159 160 371
Fusion rules 154Ч157 160
Fusion tensor product 371 552Ч555
Gabriel's theorem 307Ч308 489
Gel'fand Ч Naimark Ч Segal state 439
Gel'fand Ч Tsetlin basis 476Ч478
Generalized Cartan matrix 562
Graphs, admissible 482
Graphs, coloured oriented 482
Graphs, crystal 484
Graphs, tensor products of 483Ч486
Grothendieck group 137Ч138
Grothendieck ring 139 156
Grothendieck Ч Teichmuller group 558Ч559
Grothendieck Ч Teichmuller group and quasi-Hopf algebras 559Ч560
Group algebra 105 112 175
Group cohomology 533Ч534
Group-like 106 193
H-adic topology 105
Haar integral see integral invariant
Hamiltonian 68Ч69
Hamiltonian vector field 17
Harish Chandra homomorphism 284 290 321Ч324
Harish Chandra homomorphism and quantum coadjoint action 296
Harish Chandra's theorem 285 290
Hecke algebra 332Ч336 404 476
Hecke algebra, representations 405Ч406
Heisenberg ferromagnet see XXX model
Heisenberg group 45 218
Heisenberg Lie algebra 44Ч45 176 186
Hermitian symmetric space 41
Highest weight 314 354 383 434 441
Highest weight module 314 324 354 542
Highest weight module for QF algebras 434 441
Highest weight module for Yangians 383
Highest weight vector 314 383
Hilbert space tensor product 415
Hochschild cohomology 174 254
Homfly polynomial 497Ч498 509 517
HOMFLY polynomial for trefoil knot 498Ч499
Hopf algebra 103Ч105
Hopf algebra, *-structure 117Ч119 309Ч311 329 431Ч432
Hopf algebra, almost cocommutative 119
Hopf algebra, coboundary 123
Hopf algebra, cocommutative 102
Hopf algebra, cohomology 173Ч177
Hopf algebra, deformations 171
Hopf algebra, dual 111Ч115 131Ч132 223Ч226 234Ч235
Hopf algebra, Graded 105
Hopf algebra, integral on 115Ч116 132
Hopf algebra, quasitriangular 123 129Ч130
Hopf algebra, representations 108Ч112
Hopf algebra, ribbon 125 133
Hopf algebra, topological 105 114 123
Hopf algebra, triangular 123 150Ч151
Hopf ideal 103Ч104
Hopf link 165Ч166
Hopf's theorem 108
Hyperalgebra 304 358 359Ч360
Identity object 138
Infinite-dimensional orthogonal group 414Ч417
Infinitesimal deformation 172
integral 115Ч116
Integral form, non-restricted 289
Integral form, restricted 297
Intersection cohomology 489
Intertwiner 151 348Ч351 542
Invariant 115
Invariant bilinear form 563
Invariant bilinear form, orthogonality properties 564
Invariant differential form 245Ч246
Invariant, non-central 456
Invariant, normalized 115
Ising model 371Ч372
Jackson integral 457 467
Jacobi identity 17
Jacobson topology 454
Jets 391
Jones polynomial 168 498 500
Kac Ч Moody algebra 562
Kashiwara's tensor product algorithm 485Ч486
Kauffman polynomial 499 500 510 517
Kazhdan Ч Lusztig element 406
Kazhdan Ч Lusztig polynomial 360
Kazhdan Ч Lusztig tensor product 552Ч555
Kernel 137
Kink 501
Kirby move 503 522Ч525
Kirby move, special 503
Kirillov Ч Kostant principle see orbit principle
Knizhnik Ч Zamolodchikov equation 539Ч541
Knizhnik Ч Zamolodchikov equation and hyperplane complements 561
Knizhnik Ч Zamolodchikov equation and m-point functions 542Ч543
Knizhnik Ч Zamolodchikov equation and quantization 543Ч549 555
Knot 496
Kohno Ч Drinfel'd monodromy theorem 549Ч550
Lattice model, exactly solvable 247
Lattice model, integrable 246Ч253
Lax pair 69Ч71 73 76
Left dual 111 122
Leibniz identity 17
Length 565
Level 408Ч409
Level for affine Lie algebras 566
Lie bialgebra 24Ч33
Lie bialgebra, automorphism 32
Lie bialgebra, coboundary 50Ч59
Lie bialgebra, cocommutator of 25
Lie bialgebra, derivation 32Ч33
Lie bialgebra, double 34Ч35 58Ч59
Lie bialgebra, dual 33Ч34
Lie bialgebra, factorizable 67
Lie bialgebra, homomorphism 25
Lie bialgebra, ideal 25
Lie bialgebra, opposite 25
Lie bialgebra, pseudotriangular 56
Lie bialgebra, quasitriangular 54
Lie bialgebra, quotient 25
Lie bialgebra, standard 29Ч30 34Ч36 55Ч56 59 81 93
Lie bialgebra, tangent 26
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



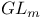
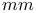 matrices
matrices 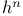 )
)