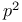|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Coutinho S. — The mathematics of ciphers: number theory and RSA cryptography |
|
|
 |
| Предметный указатель |
Abel, N.H. 127
Addition 6
Addition in elliptic curve 176
Addition, modulo n 69
Adleman, L. 3
Al jabr w'al muqabalah see "Ben Musa"
Al Khorwarazmi see "Ben Musa"
Alford, W.R. 100 104
Algebra 19
Algorithm 17 19
Algorithm, probabilistic 168 172
Aristotle 43
Arithmetic 7 8
Array 59
Ars Margna see "Cardano G."
Art of Computer Programming, The see "Knuth D.E."
Aryabhatiya 118
ASCII 164
Associativity 121
Astronomy 108
Axiom 13
Bachet, C.G. 8 9
Base 6 96 100—101
Basic principle (of equivalence classes) 64 69
Ben Musa 18 19
Berkeley, G. 175 177
Bertelsen, N. P 97
Besicovitch, A.S. 74
Bhaskara 110
big bang 37
Binomial theorem 87
Block 163
Block, fixed 171
Brilhart, J. 154
CAESAR 1
Calculus 9 19
Cardano, G. 126
Carmichael numbers 97—100 102—105
Carmichael, R.D. 97 100
Carry (of addition) 6
Catalan's Conjecture 11
Cauchy's theorem 137
Champollion, J.F. 2
Chevalier, A. 128
Chinese remainder algorithm 110 113—114 116 119
Chinese remainder theorem 111—112 114—117 119 172
Chocolate bar 19—20
Cipher 1—2
clock 69
Co-factor 23
Co-prime numbers 23 31
Co-prime numbers, pairwise 114
Cole, F.N. 143
Complex number 45 157
Composite number 33
Composite number, consecutive 46
Compositeness test 95
Composition (of symmetries) 123
Computer algebra 5
Computer algebra system 5 95 96 153 160 164
Computer algebra system, Axiom 104
Computer algebra system, Maple 103—104
Congruence in ![$\mathbb{Z}[\sqrt{3}]$](/math_tex/9341b3e6e69a22cd1796c49263e1cbe882.gif) 78 147—148 78 147—148
Congruence, linear 76—77
Congruence, modulo a subgroup 136—137 147
Congruence, modulo n 66—68
Contrapositive 14
Converse of Lagrange's theorem 137
Converse of statement 13
Coordinates (of table) 111 130
Counter-example 14
Cryptoanalysis 1 175
cryptogram 1
Cryptography 1
Cubic curve 176
Cubic equation 126
de Fermat factorization algorithm 37—40 47 168 177
de Fermat last theorem 9 45 73 176—177
de Fermat little theorem 86
de Fermat method 142 149—150
de Fermat number 51 53 61 77 141 144—146 149—150 152 177
de Fermat theorem 86—88 93—96 98 100 115 135 142—144 157 159 167
de Fermat, de Samuel 9
de Fermat, Pierre 8 10 11 45 51 73 78 79 83 84 86 93 141 149 178
de ROBERVAL, G.P. 9 78
de Valle-Poussin, C.J. 57
decryption 1 165
Decryption key 3 165 172
Diffie, W. 3
Diophantine equation 73—74 176
Diophantus 8—9 45 73—74
Dirichlet, L. 12
Discrete logarithm problem 172
Disquisitiones Arithmetics see "Gauss C.F."
Distributive property 70
Dividend 19
Divisibility criteria 71—72
Division, algorithm 17
Division, modulo n 75—77
Division, theorem 21
Divisor 19 22—23
Dyson, F.J. 177
El Gamal cryptosystem 172
Electronic signature 3 170
Elements see "Euclid"
Eletronic calculator 21 144 165
Elliptic curve 176
Elliptic curve, algorithm 176
Encryption 1
Encryption key 3 164
Equilateral triangle 123
Equilateral triangle, group of symmetries of 123—125 133
Equivalence class 64—68
Equivalence class, modulo a subgroup 137
Equivalence class, modulo n 67—68
Erathostenes 57
Euclid 8 12—13 15 17 23 41—43 52 55
Euclidean algorithm 17 22—23 47
Euclidean perfect number 47 149
Euler function see "Phi function"
Euler method 144—145 149
Euler theorem 135 139 166—167
Euler, L. 9—10 47 51—53 55—56 61 73 84 93 141 144 158 178
Exponential formulae (for prime numbers) 51—54
Extended Euclidean algorithm 27 31 40 41 75 76 108 111 165 167
Factor 22
Factorial 54
Ferrari, L. 126
Ferro, Scipione del 126
Fibonacci sequence 25 31 92
Finger-reckoning 69
Finkelstein, R. 74
Fior, A.M. 126
FRACTION 5 42—43 65—66
Franklin, B. 116
Frenicle, B. 53 83 149
Frequency analysis 1 2
Fundamental property of the prime numbers 41—44 89
Fundamental theorem of algebra 176
Fundamental Theorem of Arithmetic 33
Galois, E. 127—128 132
Gauss method 158—159 161
Gauss, C.F. 10 19 33 45 63 128 145 151 158 161 175 177
Generator (of a cyclic group) 134 158 161
Geometric picture (of 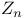 ) 68 112 130 ) 68 112 130
Geometric progression 8
Geometry 8 10 43 123
Goldbach, C. 10—11
Goldbach, conjecture 11
Gostin, G.B. 146
| Granville, A. 100 104
Great Internet Mersenne Prime Search 149
Greatest common divisor 7—8 12 22—23
Grounde of Artes, The see "Recorde R."
Group 121 176
Group of invertible elements in 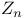 129—131 135 139 142 144 129—131 135 139 142 144
Group of invertible elements in ![$\mathbb{Z}_{q}[\sqrt{3}]$](/math_tex/2a90ea07bbc037ae48668718fcd088e882.gif) 148—150 148—150
Group of prime order 134
Group of symmetries 123—126
Group theory 53 79 121 141
Group, abelian 122 127 138 156—157 160
Group, cyclic 139 160—161
Group, dihedral 126
Group, finite 125 132 141 160—161
Hadamard, J. 57
Halter-Koch, F. 74
Hardy, G.H. 175 177—178
Hellman, M.E. 3
Herodotus 43
Hexagonal number 92
Hieroglyphs 1—2
Higly composite number 47
Horapollo of Nilopolis 2
Hypasus of Metapontum 43
Hypothesis 13
Identity element (in group) 121
Induction 83
Induction, finite 79 83
Induction, hypothesis 85 87 90
Induction, mathematical 84
Input (of algorithm) 17 19
Internet 2 176
Inverse of an element 33
Inverse of an element in a group 121
Inverse of an element, modulo n 75 77
Invertibility theorem 75—76 88 96 107
Invertible element modulo n 75 129
Invertible element modulo n, set of 76 129
Ireland, K. 178
Irrational numbers 42
Jacobi, C.G.J. 128
Key lemma 141—144 148 152 154—155 157—159
Knuth, D.E. 27
Koblitz, N. 177
Kocher, P. 177
Korselt theorem 99 155 166
Korselt, A. 98
Kraitchik, M. 177
Kummer, E. 45
Lagrange theorem 132—137 148 151—152 155 158
Lagrange to base e 57 169
Lagrange, J.L. 132 178
Least common multiple 46 156—157
Leeds 108—109
Legendre, A.M. 178
Lehmer, D.H. 146 151 154
Leibniz, G.W. 19 96
Lemma 25
Lenstra, H.W. 176
Lewis, D.J. 74
Liouville, J. 128
LIST 6
Littlewood, J.E. 62
Logarithm to base 10 63 150
Logistics 7
Logo-sillabic writing 2
Logographic writing 2
London, H. 74
Long division algorithm 21
Loop 20
Lucas test 151—154
Lucas — Lehmer test 52 143 146—149
Lucas, F.E.A. 86 146 151
Master Sun 110
Master Sun, Mathematical Manual 110 118
Mathematician's Apology, A see "Hardy G.H."
Merkle, R.C. 3
Mersenne number 12 51—53 78 86 141—143 146—150
Mersenne, M. 8—10 52 149
Miller test 100—105 155
Miller, G.L. 100
Modular arithmetic 63
Modulus 66
Multiple 22
Multiple, precision integers 6
Multiplication 7
Multiplication, modulo n 70
Multiplication, table (of a group) 125 138
Multiplicity 34
Nichomacus of Gerasa 57 110
Nickel, L. 149
Noll, c. 149
Number field sieve 176—177
Number theory 5 12—13 132 175—178
Numerical representation (of a message) 163
Operation (of a group) 121
Order of a group 122
Order of an element 134
Output (of an algorithm) 17—19
Oxford English Dictionary 17—18 42 83
Partition 65
Pascal, B. 8—9 84
Pepin test 152 161
Pepin, J.F.T. 152
Perfect numbers 8 46—47 51 149
Period 66
Pervusin, J. 52
Phi ( ) function 129—131 ) function 129—131
Pi ( ) function 56 62 168—170 ) function 56 62 168—170
Piece (of secret key) 116
Plaintext 1 163
Plato 7 43
Poincare, H. 85
Pollard, J. 177
Polygon 92 123 126 145
Polynomial 5 51 89
Polynomial, division of 91
Polynomial, equation 73 88 126 158 176
Polynomial, formulae (for prime numbers) 49—51
Pomerance C. 100 104 177
Power in a group 133
Power, algorithm 180—181
Power, modulo n 72—73 88 114—116
Primality test 154 160
Prime number 3 4 7 11 33 92
Prime number of the form 4n + 1 61—62 93
Prime number of the form 4n + 3 61—62 78 94 119
Prime number, distribution of 56—57 117 168 177
Prime number, formula 49
Prime number, infinity of 8 55—56 61
Prime number, Page (web page) 149
Prime number, theorem 99 169
Primitive root 157—158
Primitive root, theorem 99 134 151 155—156 158—159
Primorial 54
Primorial, primes 55
Principle of Finite Induction 84 90
Principles of Human Knowledge 175
Prior Analytics see "Aristotle"
Private key 165
probability 9
Programming language 5
proof 18
Proof by contradiction 41 43 54—55 74 99 140 148 152
Proof by finite induction 85—87 89—91
Proof, constructive 75 158
Proof, non-constructive existencial 14
Properties of the operations modulo n 70—71
Pseudoprimes 95—96 105
Pseudoprimes of the form 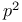 106 140 106 140
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



![$\mathbb{Z}[\sqrt{3}]$](/math_tex/9341b3e6e69a22cd1796c49263e1cbe882.gif)
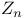 )
) ![$\mathbb{Z}_{q}[\sqrt{3}]$](/math_tex/2a90ea07bbc037ae48668718fcd088e882.gif)
 ) function
) function  ) function
) function