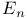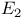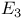|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Santalo L., Kac M. — Integral geometry and geometric probability |
|
|
 |
| Предметный указатель |
Geometric probability 105 235
Geometric probability in n.e. spaces 312
Geometric probability on the hemisphere 313
Geometric probability on the sphere 312
Geometric probability, problems 43 105—108 138—142 235 267 312
Gerriets, J. 138
Ghosh, B. 49
Giger, H. 278(228) 282(226) 291
Gilbert, E.N. 297(230) 327
Goldberg, S.I. 143
Goldman, J.R. 18
Goodman, A.W. 39
Goodman, R.E. 39
Gotz, A. 31(70)
Goudsmit, S. 58
Graev, M.I. 346 347 348
Grassmann manifolds 202
Grassmann manifolds, volume of 203
Great circles at random 329
Green, J.W. 60 347
Green, L.W. 351
Grenander, U. 294(237)
Gridgeman, N.T. 72
Griffiths, P.A. 343 344
Groemer, H. 65 210 217(243) 223
Group of affine transformations 179
Group of motions 12 160 198
Group of motions in 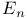 196—199 196—199
Group of motions in n.e. spaces 300
Group of motions in the plane 12 80—82
Growth rate 298
Gruenbaum, B. 1 38 350(247 248)
Grunwald, G. 123
Guenther, W.C. 100
Guggenheimer, H. 10 11 128 249 351(253 254)
Guter, R.S. 103(260)
Haar measure 157
Hadwiger's condition 121—122
Hadwiger's condition for n.e. plane 324
Hadwiger, H. 1 13 39 59(270) 60 118 121 122 124 134 138 200(274) 217 218(274) 223 226 229(271) 235 237 238 248(274) 260 275 278(274) 280 303 324 350
Hammersley, J.M. 212
Harding, E.F. 58
Heil, E. 10(296)
Helgason, S. 177(298) 345 347 348
Hemmi, D. 10
Herglotz formula 239
Herglotz formula in elliptic space 319
Herglotz, G. 239 302 319
Hermann's formulas 349
Hermann, R. 330 349
Hermitian elliptic geometry 339
Hermitian group 339
Hermitian inner product 339
Hermitian metric 340
Hilbert, D. 288(125)
Hilliard, J.E. 292(309c)
Holcomb, D.F. 213
Holditch theorem 11
Holgate, P. 24
Holomorphic curves 343
Hombu, H. 41(682)
Homogeneous affinities 181
Homogeneous spaces 165
Homogeneous spaces, density in 165 169 170
Homogeneous spaces, invariant measure in 165
Homogeneous symplectic group 344
Horneffer, K. 247
Horocycle convex sets 315
Horocycles 314
Horospheres 347
Horowitz, M. 62
Hostinsky, B. 72(318)
Hurwitz, A. 59
Hyperbolic n.e. space 300
Hyperplanes in general position 328
Hypersurface polar 303
Hypersurfaces and linear spaces 247
icosahedron 230
Ideal points 299
Independent differential forms 145 354
Inequalities for tetrahedrons 311
Inequality of Ambarcumjan 37 231
Inequality of Fary 254 255
Inequality of Feller 41
Inequality of Fenchel 254
Integral formulas 13 16 21 42 58 59 95 221 230
Integral formulas and Fourier series 59
Integral formulas in elliptic space 314 322
Integral formulas in Hermitian space 341—343
Integral geometry in complex spaces 338
Integral geometry in Riemann manifolds 330—338
Integral geometry on surfaces 350
Integral manifold 146
Integral of the power of chords 46 237
Integral of volume 258
Integrals and quermassintegrale 224—227
Integrals for cylinders 271
Integrals of a flattened convex body 227—229 243
Integrals of mean curvature 222 223
Integrals of n.e. sphere 308
Interior parallel set 8
Internal cover 32
Intersection of manifolds 258—260
Intersection of manifolds in n.e. spaces 323
Intersection, with random lines 289
Intersection, with random planes 286
Intersection, with random spheres 293
Invariant densities in homogeneous spaces 165-169
Invariant subgroups 169
Invariant volume element 156
Invariant volume element of affine groups 181
Inverse Radon transform 346
Isoperimetric deficit 119
Isoperimetric inequality 36 37 104 119 123
Isoperimetric inequality in n.e. plane 324
Isoperimetric inequality of Banchoff and Pohl 252
Isoperimetric inequality of Chakerian 232
Isotropic random simplexes 201
Isotropy group 170 173
Iwasawa, M. 213
Jacobian matrix 149
Jaglom, I.M. 1
Jakeman, A.J. 290(321 322)
John, F. 346 348
Johnson, W.A. 298
Jurtova, L.M. 195
Jusupov, D. 315
Kac, M. 72
Kelly, E. 348
Kelly, P.J. 300
Kendall, D.G. 58 137(332) 138 297(333)
Kendall, M.G. 13 24 51(335) 58 62(335) 63(335) 72 77(335) 138(335) 198(335) 212(335) 233(335) 276(335) 286(335) 290 292
Kinematic density for projective group 192
Kinematic density in 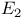 85 109—110 85 109—110
Kinematic density in 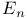 256 256
Kinematic density in n.e. spaces 304
Kinematic density, other expressions 88
Kinematic fundamental formula for convex sets 267 282
Kinematic fundamental formula for cylinders 270 277 283
Kinematic fundamental formula for strips 118 283
Kinematic fundamental formula in 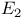 113—116 113—116
Kinematic fundamental formula in 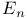 262 262
Kinematic fundamental formula in n.e. spaces 320
Kinematic fundamental formula of Chern — Federer 276
Kingman, J.F.C. 62(336) 65 201 237(337)
Klamkin, M.S. 138
Klee, V. 10 65(338)
Knight, K.F. 26
Knothe, E. 324(341)
Kobayashi, S. 143 202(341a)
| Krickeberg, K. 19 58 67
Kubota's formula 217
Kubota, T. 10 217
Kulle, R.D. 260
Kurita, M. 111(351) 170(353) 277
Langford, E. 21
Lashof, R.K. 254
Lattice points, covered by a region 137 138
Lattices in 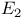 128 128
Lattices in 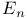 274 274
Lattices of balls 274
Lattices of convex sets 140 275
Lattices of cubes 274
Lattices of curves 134
Lattices of domains 131
Lattices of equilateral triangles 140
Lattices of figures 128
Lattices of fundamental regions 128
Lattices of points 135
Lattices of regular hexagons 133 139
Lattices of squares 133
Leaves 331
Lebesgue, H. 13 58
Left translations 81 149
Left-invariant differential forms 83 150
Legrady, K. 345
Lehner, J. 175(360)
Lekkerkerker, C.G. 10 11(361) 176(361) 190
Length of continuum of points 112
Length of curve 31 142
Length of order m 38
Lenz, H. 223
Levy, P. 24
Lie group 149
Lie transformation group 173
Line density in 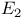 28—30 28—30
Line density in 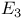 211 211
Line density, invariance by reflection 39
Line density, invariance by refraction 39
Linear graphs 42
Linear isotropy group 170
Linear search 103
Linear subspaces in 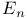 199 199
Linear subspaces through origin 185 186
Linear subspaces, intersecting a manifold 243—247
Lines intersecting a convex set 30 65
Lines intersecting curve 30
Lines that cut two convex sets 32—34
Lines that separate two convex sets 32—34
Linking numbers 251 252
Loomis, L.H. 12
Lord, R.D. 212
Luccioni, R. 193(370) 194
Lucenko, A.V. 195
Lueko, G. 63(375)
Maak, W. 31(377) 111(377 378) 247 260
Macbeath, A.M. 190
Mack, C. 101 102
Mahler, K. 10 11
Mallows, C.L. 48
Mannion, D. 25
Mantel, L. 72
Mappings of differentiable manifolds 148
Marriot, F.H. 290
Masotti Biggiogero, G. 16 21(394) 58 59(396) 231(395 397)
Masson, J. 26
Matheron, G. 19 67 290 297(399—401)
Matschinski, M. 20
Maurer — Cartan equations 152
Maurer — Cartan forms 151
Maurer — Cartan forms for affinities 180
Maurer — Cartan forms for matrix groups 153—154
McIntire, G.A. 103(104)
Mean breadth 217
Mean cross-sectional measures 217
Mean density in 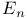 210 210
Mean distances in circle 49
Mean distances in equilateral triangle 49
Mean distances in n-ball 212
Mean distances in rectangle 49
Mean free path 42
Mean length of chords 30 60—63
Mean number of faces 295
Mean number of regions 295
Mean number of vertices 295
Mean values and curvatures 252
Mean values for convex polyhedrons 250
Mean values for integrals of mean curvature 267—269
Mean values of domains covered r times 101
Mean values of projected volumes 216
Measurable groups 177
Measure of continuum of points 260
Mehl, R.F. 298
Meijering, J.L. 297
Melzak, Z.A. 104
Miles, R.E. 17 18 19 20 23 56(414) 57 58 59(418) 65 67 100 197 198(408) 201 212 249 250(412) 290 294(199) 296 297 298 313 327 328
Minkowski and Hlawka theorem 190
Minkowski's inequality 124—125
Minkowski's theorem 176
Mixed area of Minkowski 4
Mixed convex set 4
Moments of gamma function 18
Moments of sizes of particles 291
Moran, P.A.P. 13 24 32 51(335) 62(335) 63(335) 72 77(335) 138(335) 142 198(335) 212(335) 218 233(335) 276(335) 286(335) 290 292 294(335) 327
Morgenthaler, G.W. 276(432)
Morimoto, M. 348
Morton, R.R.A. 111(434)
Morton, V.M. 211
Mostow, G.D. 177(436)
Motions in 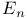 196 196
Motions in plane 80—82
Moving frames 180
Mueller, H.R. 350
Mullooly, J.P. 25(440)
Myers, E.J. 293(442)
n-dimensional Euclidean space 196
n-dimensional noneuclidean space 299
n-dimensional projective space 192 299
Nachbin, L. 157(443)
Nearly spherical particles 288 292
Neuman, F. 10(445—448)
Ney, P.E. 25
Neyman, J. 276
Nicholson, W.L. 290
Nijenhuis, A. 276
Noebeling, G. 111(455) 118 260
Nomizu, K. 143 202(341a)
Noneuclidean elliptic geometry 300
Noneuclidean hyperbolic geometry 175 300
Noneuclidean integral geometry 299
Noneuclidean motions 300
Nonseparable convex sets 39
Normal chains 340
Normal congruence 335 336
Novikoff, A.B.J. 49(457) 72 294(457)
Obrechkoff, N. 324(458)
octahedron 229
Ohmann, D. 10 217(460 461)
Orthogonal group 149 197
Orthonormal frame 196
Osculating linear spaces 343
Oshio, S. 134(464 465)
Owens, O.G. 351
Packing of segments 126
Pairs of linear spaces 205
Pairs of lines 49
Pairs of points 44 237
Palais, R.S. 331
Palasti, I. 26
Paloheimo, J.E. 103(468)
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте