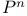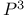|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Fulton W. Ч Intersection theory |
|
|
 |
| ѕредметный указатель |
Abel Ч Jacobi map 14 387 390
Abelian variety 14 60 219
Adjunction formula 59 289 301
Affine bundle 22
Algebraic equivalence 185Ч186 373
Algebraic scheme 6 426
Ample, line bundle 211
Ample, vector bundle 212
Ample, vector bundle, generically 217
Ample, vector bundle, n-ample 215
Analytic space 383Ч384
Arithmetic genus and Todd class 288 354 361 362
Arithmetic genus, birational invariance of 292 294
Arithmetic genus, modular law 292
Arithmetic genus, uniqueness 292 293
Associativity for intersection multiplicities 123 129
Associativity for intersection products 132
Axioms for intersection products 97 207
Basis Theorem 268Ч279 386
BezoutТs theorem for plane curves 14
BezoutТs theorem, classical version 101 144Ч152
BezoutТs theorem, refined 223Ч226
Bidegree 146
Bivariant rational equivalence class(es) for schemes 395
Bivariant rational equivalence class(es), Gysin maps for 328
Bivariant rational equivalence class(es), products of 322
Bivariant rational equivalence class(es), pull-back of 322
Bivariant rational equivalence class(es), push-forward of 322
Bivariant rational equivalence class(es), Riemann Ч Roch for 365Ч366
Blow-up 435Ч437 439
Blow-up formula 114Ч117
Borsuk Ч Ulam theorem 239Ч240
Canonical class 67 300 302
Canonical class of singular variety 77Ч79
Canonical class, divisor 60 301 432
Canonical decomposition of intersection product 94Ч95 200Ч205 218Ч226
Cap product 131
Cap product for Borel Ч Moore homology 371 374Ч375
Cap product, refined 132Ч136 324Ч326
Cartesian product 24Ч25 428
Cartier divisor(s) 29 431Ч432
Cartier divisor(s), addition of 29
Cartier divisor(s), canonical section of 432
Cartier divisor(s), effective 19Ч20 30 432
Cartier divisor(s), intersection by 33Ч41
Cartier divisor(s), line bundle of 31Ч32 432
Cartier divisor(s), linear equivalence of 30
Cartier divisor(s), local equations for 29 432
Cartier divisor(s), principal 30 432
Cartier divisor(s), representing a pseudo-divisor 31Ч32
Cartier divisor(s), support of 30Ч31 432
Cartier divisor(s), Weil divisor of 29Ч32
Castelnuovo Ч Severi inequality 311Ч312
Cellular decomposition 23 25 378
Characteristic of a family of varieties 188 Ч194
Characteristic, homomorphism 199
Characteristic, section 199
Characteristic, variety 73
Chasles Ч Cayley Ч Brill Ч Hurwitz formula 310
Chern character 56Ч57 282Ч284
Chern character in topology 367
Chern character, localized 340Ч355 363Ч366
Chern class(es) of 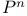 59 59
Chern class(es) of dual bundle 54
Chern class(es) of exterior power 55 265
Chern class(es) of line bundle 41Ч43 51
Chern class(es) of non-singular variety 60
Chern class(es) of normal bundle 59Ч61
Chern class(es) of P(E) 59
Chern class(es) of singular varieties 77Ч79 376Ч377
Chern class(es) of symmetric powers 57 265
Chern class(es) of tensor products 54Ч56 265
Chern class(es) of vector bundles 50Ч63 252 255Ч256
Chern class(es) of virtual bundles 57 296
Chern class(es), blowing up 298Ч303
Chern class(es), geometric construction of 252 255Ч256
Chern class(es), localized 255
Chern class(es), localized of complex 347
Chern class(es), localized, top 244Ч246
Chern class(es), MacPherson 376Ч377
Chern class(es), Mather 79
Chern class(es), polynomials in 42 53 141
Chern class(es), polynomials in positive 216
Chern class(es), total 50 60
Chern class(es), uniqueness of 53
Chern class(es), vanishing of 50 216Ч217 365 367
Chern number 293Ч294
Chern polynomial 50
Chern roots 54
Chow ring 141 (see also УIntersection ringФ)
Chow variety 16Ч17 186
circle 192
Class of hypersurfaces 84Ч85
Class of non-singular variety 84Ч85 253 261Ч262 277Ч278
Class of plane curve 188
Class of surface 193
Codimension 427
Coefficient of a variety in a cycle 11
Cohen Ч Macaulay 81 120 137 226 251 418Ч419
Cohomology for rational equivalence 143 324Ч326 331 390
Cohomology for rational equivalence with supports 325
Cohomology, operations 377
Coincidences, virtual number of 309
Commutativity for Chern classes 41 50
Commutativity for divisors 35Ч38
Commutativity for intersection multiplicities 123
Commutativity for intersection products 106Ч107 132
Compact supports for rational equivalence 184 368 378
Complete algebraic scheme 429
Complex of vector bundles 431
Complex, perfect 365Ч366
Conductor 167 289
Cone(s) 70 432Ч434
Cone(s) of sheaf 73
Cone(s), construction, for moving lemma 206
Cone(s), exact sequence of 72Ч73
Cone(s), normal 71 73 435
Cone(s), projective 432Ч434
Cone(s), projective completion of 70
Cone(s), pull-back of 433
Cone(s), Segre class of 70Ч73
Cone(s), support of 433Ч434
Cone(s), zero section of 433
Conics, plane 63Ч64 157Ч158 182Ч183 187Ч194 204 275
Conservation of number 180Ч185 193Ч194
Contribution of variety to an intersection product 94Ч95 151 224Ч225
Correspondence(s) 308Ч318 384Ч385 390Ч391
Correspondence(s) of morphism 306
Correspondence(s) on 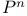 315Ч316 315Ч316
Correspondence(s) on curves 310Ч312
Correspondence(s) on Grassmannians 317
Correspondence(s) on surfaces 317
Correspondence(s), (a, b)- 309
Correspondence(s), birational 312
Correspondence(s), degenerate 308Ч309
Correspondence(s), degree (or codimension) of 308
Correspondence(s), fixed points of 315Ч318
Correspondence(s), indices (or degrees) of 309
Correspondence(s), irreducible 306
Correspondence(s), principle 310
Correspondence(s), product of 305Ч308
Correspondence(s), push-forward and pull-back of 307
Correspondence(s), ring of 307Ч308
Correspondence(s), SeveriТs formula for 317
Correspondence(s), topological 384Ч385
Correspondence(s), transpose of 306
Correspondence(s), valence of 309Ч310
Correspondence(s), Zeuthen, generalized 310
Critical point, moderate 246
Critical point, multiplicity of 124Ч125
| Curve(s), rational normal 84 156
Curve(s), tangent to given varieties 187Ч194
Cycle, class 10
Cycle, class homomorphism or map 371Ч378
Cycle, class homomorphism or map and Gysin maps 382
Cycle, class homomorphism or map and specialization 400
Cycle, class homomorphism or map and topological intersections 378Ч385
Cycle, fundamental 15
Cycle, k- 10
Cycle, non-negative, positive 10 180 211
Cycle, of subscheme 15
Deformation 198Ч200
Deformation to normal cone or bundle 86Ч91
Deformation, generic 201Ч205
Degeneracy, class 254Ч263 329 330
Degeneracy, class, positivity of 260Ч261
Degeneracy, class, symmetric and skew-symmetric 216 259Ч260
Degeneracy, locus 243
Degeneracy, locus, existence of 215Ч216
Degree of cycle or equivalence class 13
Degree of cycle or variety on P" 42 144 149Ч150
Degree of Schubert variety 274
Degree, L- 211
Depth 251Ч252 255 256 418Ч419
Determinant 409Ч412
Determinantal class 249Ч253
Determinantal formula 249Ч253
Determinantal identities 419Ч424
Determinantal locus 243 419
Differentials, relative 429Ч430
DIMENSION 427
Dimension, pure 427
Dimension, relative 429
Dimension, relative for schemes over regular base 394 396
Distinguished varieties 94Ч95 120Ч121 184 200Ч205 218Ч226 232
Double point, class 166
Double point, formula 165Ч171 289
Double point, scheme 166Ч168
Double point, set 166
Dual variety, degree of 62Ч63 84 144 169Ч170
Duality for flag manifolds 276Ч277
Duality for Grassmann bundles 267 269 270 271
Duality, Grothendieck 367Ч368
Duality, Poincare 281 328 398 440
Duality, Serre 291 368
Dynamic intersections 128 195Ч209
Enumerative geometry 187Ч194 272Ч279
Envelope, Chow envelope 356
Equivalence of connected component 153Ч160
Equivalence of variety for an intersection product 94Ч95 203Ч204
Equivalence, relations on cycles 374 385Ч392
Euler characteristic of fibres of map 245Ч246
Euler characteristic of non-singular variety 60 136 362
Euler obstruction 78 376
Exact sequence for closed and open subschemes 21Ч22 186
Exact sequence for monoidal transforms 115
Exceptional divisor 435Ч436
Excess, intersection formula 102Ч106 113 327 382
Excess, intersection of divisors 36
Excess, normal bundle 102 113 225
Extension of ground field 101Ч102 240
Exterior products 24Ч25 397
Families of cycles and cycle, classes 176Ч180 362
Fano varieties, schemes 80 217 275Ч276
Fibre, product 428
Fibre, square 428
Fixed points of correspondence, perfect 315Ч317
Fixed points of correspondence, virtual number of 315
Flag bundle 68 247Ч248
Flag manifold or variety 23 68 219 270 276Ч277 310
Flat 413 (see also УMorphism flatФ)
Function field 427
Functoriality of Gysin maps 108Ч112 113 134 330
Functoriality of intersection products 108Ч112
Functoriality of intersection products on non-singular varieties 130Ч136 141
Functoriality of push-forward and pull-back 11 18
General position 440Ч441
Genus of curve 60
Genus, Todd 60
Giambelli formula 262 265 267Ч268 271
Graph construction for complexes of vector bundles 340Ч346
Graph construction for vector bundle homomorphisms 88 347Ч348
Grassmann bundle 248Ч249 266Ч270 434
Grassmann variety 23 219 271Ч279
Grassmann variety of lines in 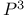 272Ч273 272Ч273
Grothendieck group of sheaves 17 281 285Ч286 354
Grothendieck group of vector bundles 57 280Ч281 294Ч295
Gysin formulas for flag bundles 247Ч248
Gysin formulas for Grassmann bundles 248Ч249
Gysin formulas for projective bundles 66
Gysin homomorphism for divisors 43Ч45
Gysin homomorphism for l.c.i. morphisms 113
Gysin homomorphism for morphisms to non-singular varieties 131 134 208
Gysin homomorphism for regular imbeddings 89Ч90 98 101
Gysin homomorphism for zero section of bundle 65Ч67 100
Gysin homomorphism or map from bivariant classes 328
Gysin homomorphism, refined 97Ч102 112Ч114 131 134
Herbrand quotients 407Ч411
Higher direct image 281
Higher K-theory 151 356 403Ч405
Hilbert Ч Samuel polynomial 42 81
Hodge theory 387Ч388
Homogeneous varieties 207 219Ч221 378 441
Homological equivalence 374 385Ч388
Homology theory for rational equivalence 10 324
Homology theory for topological K-theory 367
Homology theory, Borel Ч Moore 371 374Ч375
Hyperplane at infinity 433
Imbedding 426
Imbedding, obstructions to 60Ч61
Incidence correspondence or variety 189 273 275 277 295
Index theorem 289Ч290 388Ч389
Intermediate Jacobian 80 387 390
Intersecting with a pseudo-divisor 38
Intersecting, transversally 138 206 441
Intersection class see УIntersection productФ
Intersection class of cycle and pseudo-divisor 33 38
Intersection class, analytic 383Ч384
Intersection class, infinitesimal 199
Intersection class, positivity of 218Ч223
Intersection class, refined 94
Intersection class, topological 378 381Ч385
Intersection multiplicity or number for divisors 38Ч40 123Ч124 232Ч233 400
Intersection multiplicity or number for divisors and curves 125Ч126
Intersection multiplicity or number for plane curves 7Ч10 14
Intersection multiplicity or number of Serre 401Ч403
Intersection multiplicity or number on non-singular varieties 137Ч139 227Ч234
Intersection multiplicity or number on schemes over Dedekind rings 398
Intersection multiplicity or number on surfaces 40Ч41
Intersection multiplicity or number, fractional 125 142Ч143
Intersection multiplicity or number, uniqueness of 139 207
Intersection product and Tor 401Ч403
Intersection product for curves on a surface 60 76 95Ч96 198 203
Intersection product for divisors 111 208 224
Intersection product on 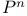 144Ч151 202Ч203 144Ч151 202Ч203
Intersection product on non-singular varieties 130Ч136
Intersection product on schemes over Dedekind rings 397Ч401
Intersection product on singular surfaces 39Ч40 125 142
Intersection product, part supported on a set 95 100Ч101 201Ч202 222
Intersection ring of 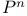 144Ч145 144Ч145
Intersection ring of algebraic scheme 324
Intersection ring of Cartesian product 141
Intersection ring of flag manifold 276Ч277
Intersection ring of Grassmann variety 270
Intersection ring of monoidal transform 142
Intersection ring of multiprojective space 146
Intersection ring of non-singular variety 140Ч144 151Ч152
Intersection ring of projective bundle 141
Intersection ring of quasi-projective scheme 143 324
Intersection ring of scheme over a Dedekind ring 397Ч399 405
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте