|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dennery P., Krzywicki A. — Mathematics for Physicists |
|
|
 |
| Предметный указатель |
Integral representations for hypergeometric function see "Hypergeometric function"
Integral representations, Cauchy's 37
Integral representations, kernels of 39 40 303
Integral representations, Poisson's 47—48
Interval, closed 5
Interval, open 5
inversion 27. see also "Conformal transformations"
Inversion of a matrix 132—133
Irregular singular point of a differential equation 292
Isolated point of a set 4
Isolated singular point of a differential equation 292
Isolated singular point of a function 22 51—52 see
Jacobi equation 212 314
Jacobi functions of the first kind 314
Jacobi functions of the second kind 315
Jacobi polynomials 207 212
Jacobi polynomials, relation to hypergeometric function 314
Jordan canonical form of a matrix 165
Jordan's lemma 56—57
Kernel of an integral operator 252
Kernel of an integral representation 39 40
Kernel of an integral representation, Cauchy's 40
Kernel of an integral representation, Euler's 303
Kernel of an integral representation, Laplace's 303
Kernel of an integral representation, Mellin 303
Kovalevska theorem see "Cauchy — Kovalevska" theorem
Kronecker delta 124
Lagrange identity 267 348
Laguerre equation 212
Laguerre polynomials 207 212
Laguerre polynomials, relation to confluent hypergeometric function 321
Laplace kernel 303 317
Laplace's equation 15
Laplace's equation in 2—dimensions with Dirichlet boundary conditions 345—346
Laplace's equation in 3—dimensions with Dirichlet or Neumann boundary conditions 355
Laplace's equation in spherical coordinates 365
Laplace's equation uniqueness of solution of 345—346 355
Laplace's equation, separation of variables 365—373
Laplace's formula 367
Laurent series 48
Lebesgue integral 184
Lebesgue measure 187—189
Legendre equation 214 316
Legendre functions, associated 366—368
Legendre functions, associated, and Gegenbauer polynomials 367
Legendre functions, associated, and spherical harmonics 368
Legendre functions, associated, orthogonality of 367
Legendre functions, of the first kind 316
Legendre polynomials 208 213—214 316 see "Spherical
Linear independence of vectors 118—119
Liouville formula 263
Lipschitz condition 258
Logarithmic function 24—25 66—69
Logarithmic function, principal logarithm 25
Logarithmic function, Riemann surface for 69
Matrix, adjoint 140
Matrix, algebra 129—132
Matrix, and change of basis 134—135 142
Matrix, canonical form of 165
Matrix, characteristic equation 158
Matrix, column 132
Matrix, definition 129
Matrix, diagonalization of 166 170
Matrix, hermitian 141 see
Matrix, inverse of 132—133
Matrix, irreducible 158
Matrix, orthogonal 152 176
Matrix, rectangular 156—157
Matrix, reducible 158
Matrix, row 138
Matrix, simultaneous diagonalization 177
Matrix, trace of 136
Matrix, transposed 140
Matrix, unit 131
Matrix, unitary 141
Maximum-minimum properties of analytic functions 41
Maximum-minimum properties of harmonic functions 42 357
Maximum-minimum properties of solutions of diffusion equation 359—360
Measure 184
Measure, Lebesgue 187—189
Mellin kernel 303
Meromorphic functions 84—86
Meromorphic functions, Mittag — Leffler expansion 84
Metric spaces 109—111 181 241
Mittag — Leffler expansion 84
Morera theorem 43
Multiplicity of a root 87
Multivalued functions 65—75
Multivalued functions, branch cut 67
Multivalued functions, branch points 67 69
Multivalued functions, integrals involving 74
Multivalued functions, Riemann sheet 69
Multivalued functions, Riemann surface 69—70 71 73
Neighborhood 4
Neumann boundary conditions 272 341 346 356
Neumann boundary conditions, exterior Neumann problems 356
Neumann boundary conditions, interior Neumann problems 356
Neumann function see "Bessel functions"
Null space of an operator 155
Null vector 104 105
Operators, adjoint 116
Operators, algebra of 113—114
Operators, bounded 241
Operators, commutation of 113
Operators, commutation of, and diagonalization of matrices 177
Operators, completely continuous see "Completely continuous operators"
Operators, differential see "Differential operators"
Operators, domain of 112
Operators, finite-dimensional 242
Operators, Green's 273 287
Operators, Hermitian see "Hermitian operators"
Operators, integral see "Integral operators"
Operators, inverse 115
Operators, left 114
Operators, linear 112
Operators, norm of 240—241
Operators, projection 117—118
Operators, range of 112
Operators, right 114
Operators, unitary 116 178
Orthogonal basis in arbitrary vector space 193
Orthogonal basis in N—dimensional space 139
Orthogonal matrix 152 176
Orthogonal polynomials 203—216
Orthogonal polynomials, differential equations for 209—210 211—215
Orthogonal polynomials, expansions in series of 215—216
Orthogonal polynomials, recurrence relations 208—209 211—215 see "Hermite" "Jacobi" "Laguerre" "Legendre" "Tchebichef
Orthogonal vectors 106
Orthogonalization, theorem 124
P-symbol (Riemann's) 304—306
Parabolic cylinder functions 321
Parabolic differential equations 336 see partial" "Diffusion
Parametric equations of a curve 18
Parseval relation 195 224
Plancherel theorem 224
Plemelj formulae 64
Point at infinity 28
| Point of accumulation 4
Point, interior 4
Point, isolated 4
Point, regular of a function 22
Point, singular of a differential equation see "Singular point of a differential equation"
Point, singular of a function see "Singular point of a function"
Poisson equation 351
Poisson equation, quasi-linear 335 337
Poisson equation, separation of variables 364—373
Poisson equation, types of 336 see "Characteristics" "Uniqueness
Poisson equation, uniqueness theorem, for diffusion equation 358
Poisson's equation 351
Poisson's integral representation 47—48
Poisson's solution of wave equation 362
Pole of an analytic function 51
Power series 23 45
Principal value of an integral 61
Pseudotensor 150
Quadratic forms 175—177
Recurrence relations for Bessel functions 325
Recurrence relations for orthogonal polynomials 208—209 211—215
Region 5 78
Region, multiply-connected 33
Region, simply-connected 33
Regular curve 18
Regular point of a function 22
Regular singular point of a differential equation 292
Representations of linear operators 128 147 251 266 269
Representations of vectors 127 136 180 249
Residues and Laurent expansion 55
Residues of a function 53
Residues, theorem of 53—54
Riemann equation 304 see
Riemann integral 185—186
Riemann P-symbol 304—306
Riemann surface see "Multivalued functions"
Riesz — Fisher theorem 190
Rodrigues formula, for Legendre polynomials 213
Rodrigues formula, generalized 205
Rotation of a vector function (curl) see "Vector analysis"
Rotations 150—151
Saddle point method see "Steepest descent method"
scalar 136
Scalar function 148
Scalar product 106 107 139 181 190 see
Schmidt orthogonalization method 125
Schwarz inequality see "Cauchy — Schwarz inequality"
Schwarz reflection principle 81
Separation of variables, method of 364—373
Series, infinite 10—11 44 see "Laurent "Taylor
Sets 1—5
Sets, accumulation point of 4
Sets, closed 5
Sets, compact, of vectors 239
Sets, difference of 2
Sets, elements of 1
Sets, empty 3
Sets, Enumerable 4
Sets, identity of 2
Sets, inclusion 2
Sets, interior point of 5
Sets, intersection of 2
Sets, isolated point of 4
Sets, nonenumerable 4
Sets, open 5
Sets, sum of 2
Singular points of a differential equation 292
Singular points of a function 22
Singular points of a function, isolated 22 51—52 69—70
Singular points of a function, isolated, branch point 67 69—70
Singular points of a function, isolated, essential singularity 51—52
Singular points of a function, isolated, pole 51
Space metric see "Metric spaces"
Space of functions, definition 180
Space, 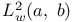 definition 190 definition 190
Space, complete 183
Space, decomposition of 159
Space, dual 108
Space, Hilbert 196—197
Space, linear vector (definition) 104
Space, n-dimensional 126—178
Space, null 155
Space, real 108 see
Spherical harmonics 368—371
Spherical harmonics and solution of Laplace's equation in spherical coordinates 373
Steepest descent, method of 87—92 328
Step function 235
Stirling's approximation for the gamma function 98
Stokes' phenomenon 321
Sturm — Liouville problem 286—288
Subspaces 117 154
Subspaces, direct sum of 161
Subspaces, invariant 155
Taylor series 45—47
Tchebichef polynomials 208 214—215
Tensor 138 143—154
Tensor, antisymmetric 147
Tensor, functions 148
Tensor, indices, contraction of 145
Tensor, indices, dummy 146
Tensor, indices, lowering and raising of 147
Tensor, metric 144
Tensor, pseudo 150
Tensor, rank of 138
Tensor, symmetric 147
Tensor, types of 138
Trace, of a matrix 136
Triangle inequality 109—110
Trigonometric functions 23—24
Trigonometrical series see "Fourier series"
Uniqueness theorems for differential equations 259 279 292 334 355
Unitary matrix 141
Unitary matrix, diagonalization of 178
Unitary operator 116
Variation of constants, method 262—263
Vector (definition) 104
Vector, algebra 104
Vector, analysis 152—154
Vector, components of 119 138
Vector, dual 107—108
Vector, length (norm) of 110
Vector, null 104—105
Vector, represented by a column matrix 132
Vector, represented by a row matrix 138
Vector, space see "Space linear
Wave equation 336 341—343 346 353—355 360—362
Wave equation, Green's function for 353
Wave equation, Poisson's solution of 362
Wave equation, uniqueness of solution of 360—362
Weber — Hermite differential equation 321
Weierstrass criterion for uniform convergence of series 11
Weierstrass theorem on essential singularities of analytic functions 52
Weierstrass theorem on term-by-term differentiation of series of analytic functions 45
Weierstrass theorem, generalized 202
Weierstrass theorem, on approximation of functions 200
wronskian 261
Zeros of analytic functions 50
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



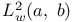 definition
definition