|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dennery P., Krzywicki A. Ч Mathematics for Physicists |
|
|
 |
| ѕредметный указатель |
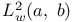 space and Hilbert space 197 space and Hilbert space 197
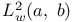 space, definition 190 space, definition 190
Accumulation point 4
Algebra of linear operators 113Ч114
Algebra of matrices 129Ч132
Algebra of vectors 104
Algebra, fundamental theorem of 86
Analytic completion 101
Analytic continuation 76Ч82
Analytic continuation, along a curve 76Ч78
Analytic continuation, basic theorem on 76
Analytic continuation, Schwarz reflection principle 81
Analytic functions 1Ч101
Analytic functions and power series 23 45
Analytic functions at a point 22
Analytic functions in a region 22
Analytic functions of several complex variables 98 334
Analytic functions, derivatives of 40
Analytic functions, local behavior of 41
Analytic functions, zeros of 50
and classification of isolated singular points 51
Associated Legendre functions see "Legendre functions"
Asymptotic expansion 92Ч93
Asymptotic expansion for Bessel functions of large argument 330
Asymptotic expansion for Bessel functions of large order 328 see method" "Stokes
Asymptotic expansion for confluent hypergeometric function 319Ч320
Asymptotic expansion for gamma function 98
Basis of a space 119 193 197
Basis of a space and set of eigenvectors of an operator 162 244 254 288
Basis of a space, change of 134
Bessel functions 322Ч332
Bessel functions and confluent hypergeometric function 322
Bessel functions of first kind 322
Bessel functions, asymptotic behavior 328
Bessel inequality 192
Bessel's equation 322
beta function 96
Bolzano Ч Weierstrass theorem 238
boundary conditions 258 334 341Ч346
Boundary conditions and types of partial differential equations 341Ч346 see "Uniqueness
Boundary conditions, adjoint 268
Boundary conditions, Cauchy's 334 346
Boundary conditions, Dirichlefs 272 341 346
Boundary conditions, homogeneous 259
Boundary conditions, inhomogeneous 260
Boundary conditions, Neumann's 272 341 346
Boundary conditions, periodic 272
Branch cut 67
Branch point 67 69Ч70
Cauchy criterion for uniform convergence 10
Cauchy theorem 34
Cauchy Ч Kovalevska theorem 334
Cauchy Ч Liouville theorem 42
Cauchy Ч Lipschitz theorem 259
Cauchy Ч Riemann conditions 15
Cauchy Ч Schwarz inequality 108 182
Cauchy's boundary conditions 334 346 see "Uniqueness
Cauchy's integral formula 37
Cayley Ч Hamilton theorem 158
Characteristic equation 158
Characteristics 336
Compact operators see "Completely continuous operators"
Compact set of vectors 239
Completely continuous operators 243 244 252Ч254 287
Completeness of a set of functions 199
complex numbers 5Ч7
Complex plane 6
Components of a vector 119 138
Components of a vector, transformation of 135 137 see
Confluent hypergeometric equation 316
Confluent hypergeometric function 317
Confluent hypergeometric function, asymptotic behavior 319Ч320
Confluent hypergeometric function, functions related to 321
Confluent hypergeometric function, integral representations 317Ч318
Confluent hypergeometric function, series representations 318
Conformal transformations 25Ч33
Conformal transformations and change of integration variable 29
Conformal transformations and point at infinity 28
Conformal transformations, conformal mapping 27
Conformal transformations, homographic transformations 27Ч29
Continuity of a function 9
Contour integrals 18Ч21
Contour integrals and calculus of residues 53Ч60
Contour integrals and Riemann integrals 20 see "Cauchy "Darboux
Contour integrals of multivalued functions 74Ч75
Contour integrals, change of integration variable 29
Contraction of tensors 145
Convergence of sequence of functions 9
Convergence of sequence of functions, uniform 9
Convergence of sequence of functionsin the mean 191
Darboux inequality 21
Delta function 235Ч237
Delta function in NЧdimensions 346Ч347 see
Delta, Kronecker's 124
Difference equations 254
Differentiability of functions of a complex variable 12Ч16
Differentiability of functions of a complex variable, Cauchy Ч Riemann conditions 15
Differentiability of functions of a complex variable, sufficiency conditions for 15
Differential equations, for Laplace equation 345Ч346 355
Differential equations, for wave equation 360 see
Differential equations, ordinary 257Ч332
Differential equations, ordinary, boundary conditions see "Boundary conditions"
Differential equations, ordinary, Cauchy Ч Lipschitz theorem 259
Differential equations, ordinary, homogeneous 257
Differential equations, ordinary, inhomogeneous 257
Differential equations, ordinary, linear 257
Differential equations, ordinary, second order of Fuchs type 303
Differential equations, ordinary, second order, Bessel 322
Differential equations, ordinary, second order, confluent hypergeometric 316
Differential equations, ordinary, second order, fundamental set of solutions 262
Differential equations, ordinary, second order, Gegenbauer 213 315
Differential equations, ordinary, second order, Green's functions see "Green's functions"
Differential equations, ordinary, second order, Hermite 211 295Ч296
Differential equations, ordinary, second order, hypergeometric 306
Differential equations, ordinary, second order, indicial equation 297Ч298
Differential equations, ordinary, second order, integral representations, method of solution 301Ч303 308 317 325
Differential equations, ordinary, second order, Jacobi 212 314
Differential equations, ordinary, second order, linear 260Ч332
Differential equations, ordinary, second order, Riemann 304
Differential equations, ordinary, second order, series solution about ordinary point 292
Differential equations, ordinary, second order, series solution about regular singular point 296
Differential equations, ordinary, second order, singular points, classification 291Ч292
Differential equations, ordinary, second order, Weber Ч Hermite 321
Differential equations, partial 333Ч373
Differential equations, partial, boundary conditions see "Boundary conditions"
Differential equations, partial, Cauchy Ч Kovalevska theorem 334
Differential equations, partial, characteristics 336
Differential equations, partial, diffusion equation see "Diffusion equation"
Differential equations, partial, Green's functions see "Green's functions"
Differential equations, partial, images, method of 362
Differential equations, partial, Laplace equation see "Laplace equation"
Differential equations, partial, linear 333
Differential equations, Partial, order of 333
Differential equations, wave equation see "Wave equation"
Differential operators 255 266Ч267 269Ч272 286
Differential operators, domain of 116 269Ч270
Differential operators, formal 266
Differential operators, formal adjoint 267
Differential operators, Hermitian 270 272 286
Differential operators, self-adjoint 267Ч272
Differential operators, separable 365
Diffusion equation 336 344 352 358
Diffusion equation, Green's function for 352Ч353
Diffusion equation, uniqueness of solution of 358
Dimension of a linear vector space 119
Dirichlet boundary conditions 272 341 346
Dirichlet boundary conditions and solution of Laplace's equation in spherical coordinates 372Ч373
Dirichlet boundary conditions, exterior Dirichlet problem 355 372Ч373
Dirichlet boundary conditions, interior Dirichlet problem 345Ч346 355 362Ч364 372Ч373
Dispersion relations 82
| Distance 109Ч111 181Ч183 see
Distributions see "Generalized functions"
Divergence of a vector function see "Vector analysis"
Dual space 108
Dual vectors 107Ч108
Eigenvalue 120
Eigenvalue equation 119Ч120 161Ч162 166 170 244 254 286Ч288
Eigenvalue equation, generalized 121 see
Eigenvalue, generalized 121 see
Eigenvector 120
Eigenvector, generalized 121 see
Einstein summation convention 128
Elliptic differential equations 336 see partial" "Harmonic "Laplace "Poisson
Entire functions 22 see
Error function 322
Essential singularity of a function, isolated 51Ч52
Euler kernel 303 308
Euler's integral, of first kind 96
Euler's integral, of second kind 95 see
Expansions of functions in Fourier series 216Ч223
Expansions of functions in Fourier Ч Bessel series 332
Expansions of functions in orthogonal series, general theory 191Ч196
Expansions of functions in series of orthogonal polynomials 215Ч216
Expansions of functions in series of spherical harmonics 369
Exponential function 23
Fourier coefficients 195
Fourier series 216Ч223
Fourier transforms 223Ч225
Fourier transforms in NЧdimensions 346
Fourier transforms of generalized functions 232
Fourier Ч Bessel series 332
Fourier Ч Bessel series of imaginary argument 324
Fourier Ч Bessel series of second kind or Neumann functions 323
Fourier Ч Bessel series of third kind or Hankel functions 324
Fourier Ч Bessel series, generating function for 326
Fourier Ч Bessel series, integral representations for 325
Fourier Ч Bessel series, modified 324
Fourier Ч Bessel series, recurrence relations between 325
Fourier Ч Bessel series, series representations 322
FourierЧBessel series 332
Fuchsian equations 303 see "Riemann
Function space, definition 180 see " b)$"/>
Functional, linear 107
Functions (definition) 8
Functions, analytic (definition) 22 see
Functions, Bessel see "Bessel functions"
Functions, beta 96
Functions, confluent hypergeometric see "Confluent hypergeometric function"
Functions, continuity of 9
Functions, delta see "Delta function"
Functions, differentiable 12Ч17
Functions, entire 22
Functions, equivalent 191
Functions, exponential and related 23
Functions, fairly good 227
Functions, gamma see "Gamma function"
Functions, Gegenbauer 315
Functions, generalized see "Generalized functions"
Functions, good 227
Functions, Green's see "Green's functions"
Functions, Hankel see "Bessel functions"
Functions, harmonic 15 356Ч357
Functions, hyperbolic 24
Functions, hypergeometric see "Hypergeometric function"
Functions, invariant 148
Functions, Jacobi see "Jacobi functions"
Functions, Legendre see "Legendre functions"
Functions, logarithmic 24Ч25 66Ч70
Functions, meromorphic see "Meromorphic functions"
Functions, multivalued see "Multivalued functions"
Functions, Neumann see "Bessel functions"
Functions, of complex argument 11
Functions, of several complex variables 98Ч101
Functions, orthogonal expansions of see "Expansions of functions"
Functions, parabolic cylinder 321
Functions, polynomials 22 203Ч216 also "Orthogonal
Functions, primitive 20
Functions, single-valued 21
Functions, tensor 148
Functions, WEIGHT 181 203 207Ч208 267 272
Fundamental theorem of algebra 86
Fundamental theorem of integral calculus 20
Gamma function 94Ч98
Gamma function, asymptotic behavior, Stirling's approximation 98
Gamma function, integral representations 94 95
Gauss' integral 58Ч59
Gauss' theorem, in 3 dimensions 356
Gauss' theorem, in N dimensions 348
Gegenbauer equation 213 315
Gegenbauer function 315
Gegenbauer polynomials 208 213
Gegenbauer polynomials, relation to associated Legendre functions 367
Gegenbauer polynomials, relation to hypergeometric function 315
Generalized functions 225Ч237
Generalized functions, delta function 235Ч237
Generalized functions, differentiation of 231
Generalized functions, Fourier transform of 232
Generalized functions, local value of 229
Gradient 17 see
Green's functions 273Ч291 348Ч355 362Ч364
Green's functions for linear partial differential equations with constant coefficients 351Ч355
Green's functions for partial differential equations 348Ч355 362Ч364
Green's functions for second order ordinary linear differential equations 273Ч291
Green's functions, adjoint 274
Green's functions, diffusion equation 352Ч353
Green's functions, eigenfunction expansion 288
Green's functions, generalized 284
Green's functions, Poisson's equation 351Ч352
Green's functions, singular part of 350Ч355
Green's functions, wave equation 353Ч355
Green's identities, first and second 356
Green's identity 269 349
Green's identity, generalized 267 348
Hamilton Ч Cayley theorem 158
Hankel functions see Bessel functions
Harmonic functions 15 356Ч357
Hermite polynomials 207 211 321
Hermite's equation 211 295Ч296
Hermitian matrices 141 170Ч178
Hermitian matrices, diagonalization of 170Ч175
Hermitian matrices, simultaneous diagonalization of two 177Ч178
Hermitian operators 116 120 124
Hermitian operators, completely continuous 244
Hermitian operators, differential 270 272 286Ч288
Hermitian operators, eigenvalue equations for 120Ч121 124 170 244 254 286Ч288
Hermitian operators, integral 252 254
Hilbert space 196Ч197 see " b)$"/>
Hilbert theorem on integral operators 254
Homographic transformations 27Ч29 see
Hyperbolic differential equations 336 see partial" "Wave
Hypergeometric equation 306
Hypergeometric equation, Kummer's solutions of 307
Hypergeometric equation, Riemann P-symbol 304Ч306 see "Hypergeometric "Riemann
Hypergeometric function 306Ч316
Hypergeometric function, Euler formula 310
Hypergeometric function, integral representations for 308Ч312
Hypergeometric function, related functions 314Ч316
Hypergeometric function, relations between 312Ч314
Hypergeometric function, symmetry property of 307
Hypergeometric series 306Ч307 see
Images, method of 362
Indicial equation 298
Infinity, point at 28
integral see "Contour integrals" "Lebesgue "Riemann
Integral operators 251Ч254 273 287
Integral representations 39 40 301
Integral representations and solutions of differential equations 301
Integral representations for Bessel functions see Bessel functions
Integral representations for confluent hypergeometric function see "Confluent hypergeometric function"
Integral representations for gamma function see "Gamma function"
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



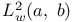 space and Hilbert space
space and Hilbert space