Авторизация
Поиск по указателям
Reiner I. — Representation theory of finite groups and related topics (Proceedings of symposia in pure mathematics)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Representation theory of finite groups and related topics (Proceedings of symposia in pure mathematics)Автор: Reiner I. Аннотация: The study of the mapping class group Mod(S) is a classical topic that is experiencing a renaissance. It lies at the juncture of geometry, topology, and group theory. This book explains as many important theorems, examples, and techniques as possible, quickly and directly, while at the same time giving full details and keeping the text nearly self-contained. The book is suitable for graduate students.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1971Количество страниц: 185Добавлена в каталог: 16.04.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
68 19 21 22 21 22 20 107 117 155 29 30 1-1 condition 141 Abelian normal subgroup 37 Adams operations 156 Adjoints to restriction 42 Admissible lattice 169 Admissible lattice, irreducibility criterion 170 Admissible transformations 113 Affine group 146 Algebra 111 Algebra, bounded type 111 Algebra, finite type 111 Algebra, indecomposable representations 111 Algebra, matrix questions 113 Algebra, polynomial part 120 Algebra, strongly unbounded type 111 Algebra, unbounded type 111 Algebraic maps 39 40 42 43 Algebraic maps, transfer 42 44 Alternating form 73 Alternating group 95 Automorphism 25 Automorphism (B,N) pair 91 Basic set 8 Bass-order 130 137—142 Bass-order, completely primary 133 Bass-ring 131 137 Block, type of block 10 Bounded type 111 Brauer characters 124 Brauer homomorphism 140 Brauer's first fundamental theorem 141 Brauer's second fundamental theorem 142 Brauer's second main theorem on blocks 124 Cancellation 85 Cancellation for modules 31 Category of G-functors 42 Character ring functor 58 Character table 97 Characteristic powers 1 Characterization of characters 124 Characters 49 51 Characters, Brauer characters 124 Characters, character table 97 Characters, characterization of characters 124 Characters, extension of character 51 Characters, invariant 51 Characters, irreducible 3 80—82 146 Characters, orthogonality relations 49 Characters, permutation 73 Characters, principal indecomposable 123 Characters, q-modular (Brauer) 97 Chevalley groups 1 Chevalley groups, finite 13 Chevalley groups, Hecke algebra 2 Chevalley groups, irreducible representation 13 169 Cohomology ring functor 59 Completely primary Bass-order 133 Compounds 92 Conjugacy classes 51 78 Contravariant form 170 Conway group 108 Cusp form 150 Decomposition matrix 124 Decomposition numbers 138 Defect 0 and 1 142 Defect base 60 Defect group 61 139 Defect-basis 44 Doubly transitive group 67 Exchange property 30 Exponentials 40 Extension of character 51 F.C. subgroup 117 Factorizable groups 77 Fields of characteristic p 99 Finite Chevalley groups 13 Finite groups, 68 Finite groups, 20 Finite groups, 107 Finite groups, (B,N) pair 91 Finite groups, 1-1 condition 141 Finite groups, adjoints to restriction 42 Finite groups, algebraic maps 39 40 42 43 Finite groups, alternating group 95 Finite groups, automorphism 25 Finite groups, basic set 8 Finite groups, Brauer homomorphism 140 Finite groups, Chevalley groups 1 Finite groups, Conjugacy classes 51 78 Finite groups, Conway group 108 Finite groups, doubly transitive group 67 Finite groups, exponentials 40 Finite groups, fixed point subgroup 25 Finite groups, G-functor 42 43 44 57 124 Finite groups, generalized quaternion groups 74 Finite groups, GL(n,C) 37 Finite groups, Hecke algebra 91 Finite groups, hyperelementary groups 97 Finite groups, indecomposable representations 89 Finite groups, index parameters of G 91 Finite groups, integral representation ring 173 Finite groups, leech lattice 108 Finite groups, linear group 37 Finite groups, metacyclic groups 65 79 Finite groups, nonsimplicity 47 Finite groups, onto condition 141 Finite groups, permutation character 73 Finite groups, projective oG-modules 88 Finite groups, real representations 66 Finite groups, reflection representation 92 Finite groups, relative Grothendieck rings 44 99 Finite groups, representation modules 165 166 Finite groups, representations of finite groups 99 Finite groups, Suzuki group 107 Finite groups, sylow 2-subgroups of simple groups 53 Finite groups, units in 41 Finite groups, X-graded Clifford system 20 Finite type 111 Fixed point subgroup 25 Frobenius algebra 49 Frobenius algebra, characters 49 Frobenius — Schur formula 98 Frobenius-Schur formula 98 Fundamental module 89 G-algebra 59 G-functor 42 43 44 57 124 G-functor, category of G-functors 42 G-functor, character ring functor 58 G-functor, cohomology ring functor 59 G-functor, defect base 60 G-functor, defect group 61 139 G-functor, G-algebra 59 G-functor, Grothendieck ring functors 59 G-functor, subgroup category 58 G-functor, transfer theorem 61 Genera of R-lattices 85 Generalized polynomial identity 119 Generalized quaterion groups 74 Generic degree 2 Generic ring 1 92 Genus 85 Genus, restricted genus 87 GL(n,C) 37 Gorenstein-ring 131—133 137 138 Green's polynomials 149 Grothendieck ring functors 59 Group ring 117 Group, Lie 13 Group, primitive 37 Group, simple 13 161 Hecke algebra 2 91 Hyperelementary groups 97 Indecomposable lattice 137 140 Indecomposable representations 89 111 Indecomposable representations, infinite type 111 Index parameters of G 91 Induction theorems 44 45 Infinite type 111 Integral representation 85 Integral representation ring 173 Invariant character 51 Invariant character, 124 Invariant character, parabolic type 3 Irreducibility criterion 170 Irreducible character 3 80-82 146 Irreducible character, generic degree 2 Irreducible character, green's polynomials 149 Irreducible representation 13 169 Isomorphic refinements 30 Krull — Schmidt (— Azumaya) theorem 29 Lattice, cancellation 85 Lattice, genera of R-lattices 85 Lattice, genus 85 Lattice, indecomposable 137 140 Lattice, local direct factor of M 87 Leech lattice 108 Lie algebra Cusp form 150 Lie groups 13 Linear group 37 Local direct factor M 87 Matrix questions 113 Matrix questions, admissible transformations 113 Metacyclic groups 65 79 Metacyclic groups, split 65 Modular theory of permutation representations 137 Modules, 21 22 Modules, 21 22 Modules, 29 Modules, admissible lattice 169 Modules, Brauer's first fundamental theorem 141 Modules, cancellation for modules 31 Modules, contravariant form 170 Modules, decomposition numbers 138 Modules, defect 0 and 1 142 Modules, exchange property 30 Modules, fundamental 89 Modules, Krull — Schmidt (— Azumaya) theorem 29 Modules, Schur index 97 Modules, tensor product theorem 171 Modules, vertex 165 166 Nilpotent radical 118 Nonsimplicity 47 O-order 85 Onto condition 141 Order, bass-order 130 137 142 Order, integral representation 85 Orthogonal idempotent decomposition 166 167 Orthogonality relations 49 Orthogonality relations, 124 Orthogonality relations, Brauer's second main theorem on blocks 124 Parabolic type 3 Parabolic type, partially ordered set 114 Permutation character 73 Polynomial identity 118 Polynomial part 120 Prime rings 117 primitive 37 primitive 37 Principal indecomposable characters 123 Principal indecomposable characters 123 Projective ideal 166 Projective ideal 166 Projective ideal, orthogonal idempotent decomposition 166 167 Projective oG-modules 88 Projective oG-modules 88 q-modular (Brauer) character 97 Real representations 66 Real representations 66 Reflection representation 92 Reflection representation 92 Reflection representation, compounds 92 Reflection representation, compounds 92 Relative Grothendieck rings 44 99 Relative Grothendieck rings 44 99 Relative Grothendieck rings, Defect-basis 44 Relative Grothendieck rings, Defect-basis 44 Relative Grothendieck rings, induction theorems 44 45 Relative Grothendieck rings, induction theorems 44 45 Representation algebra 165 Representation algebra 165 Representation modules 65 66 Representation modules 65 66 Representation modules, projective ideal 166 Representation modules, representation algebra 165 Representation of finite groups 99 Representation of finite groups 99 Representation of finite groups, modular theory of permutation representations 137 Restricted genus 87 Restricted genus 87 Ring, 117 Ring, 117 Ring, 155 Ring, 155 Ring, Adams operations 156 Ring, Adams operations 156 Ring, bass-ring 131 137 Ring, bass-ring 131 137 Ring, Generalized polynomial identity 119 Ring, Gorenstein-ring 131—133 137 138 Ring, group ring 117 Ring, integral representation ring 173 Ring, integral representation ring 173 Ring, o-order 85 Ring, o-order 85 Ring, polynomial identity 118 Ring, polynomial identity 118 Ring, prime 117 Ring, prime 117 Ring, semiprime 118 Ring, semisimple 120 Ring, semisimple 120 Ring, splitting principle 155 Schur index 97 Schur index 97 Semiprime rings 118 Semiprime rings, nilpotent radical 118 Semisimple rings 120 Semisimple rings 120 Semisimple rings sets of primes 123 Semisimple rings sets of primes 123 Simple groups 13 162 Simple groups 13 162 Split metacyclic groups 65 Split metacyclic groups 65 Splitting principle 155 Splitting principle 155 Strongly embedded subgroup 69 Strongly embedded subgroup 69 Strongly unbounded type 111 Subgroup category 58
Реклама
 |
|
О проекте
|
|
О проекте



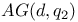
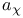 =
= 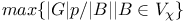
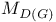 (M-homogeneous)
(M-homogeneous) 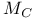 (
(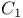 -free)
-free) 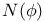
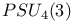
 -theorem
-theorem  -ring
-ring 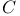 -decomposition
-decomposition 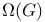
 -blocks
-blocks  -theorem
-theorem