Авторизация
Поиск по указателям
Apostol T. — Mathematical Analysis, Second Edition
Обсудите книгу на научном форуме Нашли опечатку?
Название: Mathematical Analysis, Second EditionАвтор: Apostol T. Аннотация: It provides a transition from elementary calculus to advanced courses in real and complex function theory and introduces the reader to some of the abstract thinking that pervades modern analysis.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2Год издания: 1974Количество страниц: 492Добавлена в каталог: 17.03.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
47 33 438 192 457 61 14 367 115 116 371 241 142 141 93 328 35 104 114 117 344 261 44 81 254 37 368 232 293 295 294 445 459 14 2 47 54 62 347 49 129 4 150 54 62 41 40 41 289 1 32 389 407 436 134 93 128 141 290 348 98 170 98 170 64 1 33 396 294 295 48 (a,+ 4 (a,b), [a,b], n-dimensional open (closed) interval 50 52 (a,b), [a,b], open (closed) interval with endpoints a and b 4 (f,g), inner product of functions f and g, in 294 295 (M,d), metric space M with metric d 60 a.e., almost everywhere 172 Abel, limit theorem 245 Abel, Neils Henrik, (1802-1829) 194 245 248 Abel, partial summation formula 194 Abel, test for convergence of series 194 248 Absolute convergence, of products 208 Absolute convergence, of series 189 Absolute value 13 18 Absolutely continuous function 139 Accumulation point 52 62 Additive function 45 Additivity of Lebesgue measure 291 Adherent point 52 62 Algebraic number 45 Almost everywhere 172 391 Analytic function 434 Annulus 438 Approximation theorem of Weierstrass 322 ARC 88 435 Arc length 134 Archimedean property of real numbers 10 Arcwise connected set 88 Area (content) of a plane region 396 Argand, Jean-Robert (1768-1822) 17 Argument of complex number 21 Arithmetic mean 205 Arzela, Cesare (1847-1912) 228 273 Arzela’s theorem 228 273 Associative law 2 16 Axioms for real numbers 1 2 9 B(a), B(a;r), open n-ball with center a, (radius r) 49 B-A, the set of points B but not in A 41 Ball, in 49 Ball, in a metric space 61 Basis vectors 49 Bernoulli, James (1654-1705) 251 338 478 Bernoulli, numbers 251 Bernoulli, periodic functions 338 Bernoulli, polynomials 251 478 Bernstein's theorem 242 Bernstein, Sergei Natanovic (1880-1968) 242 Bessel function 475 Bessel inequality 309 Bessel, Friedrich Wilhelm (1784-1846) 309 475 beta function 331 Binary system 225 Binomial series 244 Bolzano — Weierstrass theorem 54 Bolzano's theorem 85 Bolzano, Bernard (1781-1848) 54 85 Bonnet, Ossian (1319-1892) 165 Bonnet’s theorem 165 Borel, Emile (1871-1938) 58 Bound, greatest lower 9 Bound, least upper 9 Bound, lower 8 Bound, uniform 221 Bound, upper 8 Boundary, of a set 64 Boundary, point 64 Bounded, away from zero 130 Bounded, convergence 227 273 Bounded, function 83 Bounded, set 54 63 Bounded, variation 128 c(S), Jordan content of S 397 C, the set of complex numbers, the complex plane 16 Cantor intersection theorem 56 Cantor set 180 Cantor — Bendixon theorem 67 Cantor, Georg (1845-1918) 8 32 56 67 180 312 cardinal number 38 Carleson, Lennart 312 Cartesian product 33 Casorati — Weierstrass theorem 475 Cauchy condition, for products 207 Cauchy condition, for sequences 73 183 Cauchy condition, for series 186 Cauchy condition, for uniform convergence 222 223 Cauchy — Riemann equations 118 Cauchy — Schwarz inequality, for inner products 294 Cauchy — Schwarz inequality, for integrals 177 294 Cauchy — Schwarz inequality, for sums 14 27 30 Cauchy, Augustin-Louis (1789-1857) 14 73 118 177 183 207 222 Cauchy, inequalities 451 Cauchy, integral formula 443 Cauchy, integral theorem 439 Cauchy, principal value 277 Cauchy, product 204 Cauchy, Residue Theorem 460 Cauchy, sequence 73 Cesaro, Ernesto (1859-1906) 205 320 Cesaro, sum 205 Cesaro, summability of Fourier series 320 Chain rule, complex functions 117 Chain rule, matrix form of 353 Chain rule, real functions 107 Chain rule, vector-valued functions 114 Change of variables, in a Lebesgue integral 262 Change of variables, in a multiple Lebesgue integral 421 Change of variables, in a Riemann integral 164 Change of variables, in a Riemann — Stieltjes integral 144 Characteristic function 289 Circuit 435 Closed, ball 67 Closed, curve 435 Closed, interval 4 52 Closed, mapping 99 Closed, region 90 Closed, set 53 62 Closure of a set 53 Commutative law 2 16 Compact set 59 63 Comparison Test 190 Complement 41 Complete metric space 74 Complete orthonormal set 336 Completeness axiom 9 Complex number 15 Complex plane 17 Component of a metric space 87 Component of a vector 47 Component, interval 51 Composite function 37 Condensation point 67 Conditional convergent series 189 Conditional convergent series, rearrangement of 197 Conformal mapping 471 Conjugate complex number 28 Connected, metric space 86 Connected, set 86 Content 396 Continuity 78 Continuity, uniform 90 Continuously differentiable function 371 Contour integral 436 Contraction, constant 92 Contraction, fixed-point theorem 92 Contraction, mapping 92 Convergence in a metric space 70 Convergence of a product 207 Convergence of a sequence 183 Convergence of a series 185 Convergence, absolute 189 Convergence, bounded 227 Convergence, conditional 189 Convergence, mean 232 Convergence, pointwise 218 Convergence, uniform 221 Converse of a relation 36 Convex set 66 Convolution integral 328 Convolution theorem, for Fourier transforms 329 Convolution theorem, for Laplace transforms 342 Coordinate transformation 417 Countable additivity 291 Countable set 39 Covering of a set 56 Covering theorem, Heine — Borel 58 Covering theorem, Lindeloef 57 Cramer’s Rule 367 Curve, closed 435 Curve, Jordan 435 Curve, piecewise-smooth 435 Curve, rectifiable 134 d(x,y), distance from x to y in metric space 60 Daniell, P.J. (1889-1946) 252 Darboux, Gaston (1842-1917) 152 de la Vallee-Poussin, C.J.(1866-1962) 312 de Moivre, Ham (1667-1754) 29 De Moivre’s Theorem 29 Decimals 11 12 27 Dedekind, Richard (1831-1916) 8 Deleted neighborhood 457 Dense set 68 Denumerable set 39 Derivative(s), directional 344 Derivative(s), of complex functions 117 Derivative(s), of real-valued functions 104 Derivative(s), of vector-valued functions 114 Derivative(s), partial 115 Derivative(s), total 347 Derived set 54 62 Determinant 367 Df(c), Jacobian matrix of f at c 351 Difference of two sets 41 Differentiation, of integrals 162 167 Differentiation, of sequences 229 Differentiation, of series 230 Dini's theorem, on Fourier series 319 Dini's theorem, on uniform convergence 248 Dini, Ulisse (1845-1918) 248 312 319 Directional derivative 344 Dirichlet's test, for convergence of series 194 Dirichlet's test, for uniform convergence of series 230 Dirichlet, integrals 314 Dirichlet, kernel 317 Dirichlet, Peter Gustav Lejeune (1805-1859) 194 205 215 230 317 464 Dirichlet, product 205 Dirichlet, series 215 disconnected set 86 Discontinuity 93 Discrete metric space 61 Disjoint sets 41 Disjoint sets, collection of 42 Disk 49 Disk, of convergence 234 Distance function (metric) 60 Distributive law 2 16 Divergent, product 207 Divergent, sequence 183 Divergent, series 185 Divisor 4 Divisor, greatest common 5 Domain (open region) 90 Domain of a function 34 Dominated Convergence Theorem 270 Dot product 48 Double sequence 199 Double series 200 Double, integral 390 407 du Bois-Reymond, Paul (1831-1889) 312 Duplication formula for the Gamma function 341 e, irrationality of 7 Element of a set 32 Empty set 33 Equivalence, of paths 136 Equivalence, relation 43 Essential singularity 458 Euclidean, metric 48 61 Euclidean, space 47 Euclid’s lemma 5 Euler, Leonard (1707-1783) 149 192 209 365 Euler’s, constant 192 Euler’s, product for 209 Euler’s, summation formula 149 Euler’s, theorem on homogeneous functions 365 Exponential form, of Fourier integral theorem 325
Реклама
 |
|
О проекте
|
|
О проекте



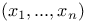 , point in
, point in 
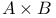 , cartesian product of A and B
, cartesian product of A and B 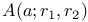 , annulus with center a
, annulus with center a 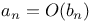 ,
, 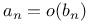 , big oh (little oh) notation
, big oh (little oh) notation 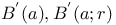 , deleted neighborhood of a
, deleted neighborhood of a 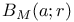 , ball in metric space M
, ball in metric space M 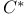 , extended complex-number system
, extended complex-number system ![$det[a_{ij}]$](/math_tex/afa82545151175751228db98281d303982.gif) , determinant of matrix [
, determinant of matrix [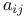 ]
] 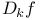 , pertial derivative of f with respect to the kth coordinate
, pertial derivative of f with respect to the kth coordinate 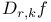 , second-order partial derivative
, second-order partial derivative 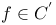 , the components of f have continuous first-order partials
, the components of f have continuous first-order partials 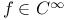 , f has derivatives of every order
, f has derivatives of every order 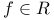 on [a,b], f is Riemann-integrable on [a,b]
on [a,b], f is Riemann-integrable on [a,b] 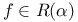 , on [a,b], f is Riemann-integrable with respect to
, on [a,b], f is Riemann-integrable with respect to  on [a,b]
on [a,b] 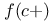 ,
, 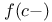 , right- (left-)hand limit of f at c
, right- (left-)hand limit of f at c 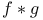 , convolution of f and g
, convolution of f and g 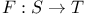 , function from S to T
, function from S to T 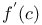 , derivative of f at c
, derivative of f at c 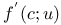 , directional derivative of f at c in the direction u
, directional derivative of f at c in the direction u 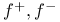 , positive (negative) part of a function f
, positive (negative) part of a function f 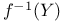 , inverse image of Y under f
, inverse image of Y under f  a.e. on S, sequence {
a.e. on S, sequence {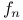 } increases on S and convergs to f a.e. on S
} increases on S and convergs to f a.e. on S 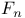 , sequence whose nth term is
, sequence whose nth term is 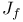 , Jacobian determinant of f
, Jacobian determinant of f 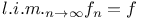 , {$f_{n}} converges in the mean to f
, {$f_{n}} converges in the mean to f 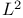 -norm
-norm 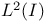 , set of square-integrable functions on I
, set of square-integrable functions on I 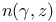 , winding number of a circuit
, winding number of a circuit  with respect to z
with respect to z 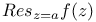 , residue of f at a
, residue of f at a 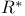 , extended real-number system
, extended real-number system 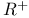 ,
, 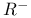 , set of positive (negative) numbers
, set of positive (negative) numbers 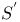 , set of accumulation points of S
, set of accumulation points of S 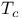 ,
, 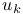 , kth-unit coordinate vector
, kth-unit coordinate vector 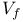 , total variation of f
, total variation of f 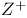 , set of positive integers
, set of positive integers 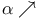 on [a,b],
on [a,b], 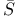 , closure of S
, closure of S 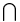 ,
, 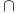 , intersection
, intersection 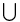 ,
, 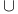 , union
, union 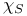 , characteristic function of S
, characteristic function of S 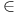 ,
, 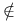 , belongs to (does not belong to)
, belongs to (does not belong to) 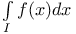 , multiple integral
, multiple integral 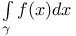 , contour integral of f along
, contour integral of f along 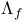 , lenght of a rectifiable path f
, lenght of a rectifiable path f 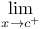 ,
, 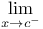 , right- (left-)hand limit
, right- (left-)hand limit ![$\mathcal P[a,b]$](/math_tex/916f0b029096f1649e08418a76896e5f82.gif) , set of all partitions of [a,b]
, set of all partitions of [a,b] 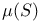 , Lebesgue measure of S
, Lebesgue measure of S 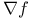 , gradient vector of f
, gradient vector of f 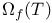 , oscillation of f on a set T
, oscillation of f on a set T 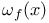 , oscillation of f at a point x
, oscillation of f at a point x 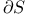 , boundary of a set S
, boundary of a set S 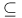 , is a subset of
, is a subset of 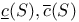 , inner (outer) Jordan content of S
, inner (outer) Jordan content of S 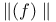 ,
, 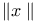 , norm or lenght of a vector
, norm or lenght of a vector  ), [a, +
), [a, +