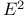Авторизация
Поиск по указателям
Hsiung C.-C. — A first course in differential geometry
Обсудите книгу на научном форуме Нашли опечатку?
Название: A first course in differential geometryАвтор: Hsiung C.-C. Аннотация: The origins of differential geometry go back to the early days of the differential calculus, when one of the fundamental problems was the determination of the tangent to a curve. With the development of the calculus, additional geometric applications were obtained. The principal contributors in this early period were Leonhard Euler (1707- 1783), GaspardMonge(1746-1818), Joseph Louis Lagrange (1736-1813), and AugustinCauchy (1789-1857). A decisive step forward was taken by Karl FriedrichGauss (1777-1855) with his development of the intrinsic geometryon a surface. This idea of Gauss was generalized to n( > 3)-dimensional spaceby Bernhard Riemann (1826- 1866), thus giving rise to the geometry that bears his name. This book is designed to introduce differential geometry to beginning graduate students as well as advanced undergraduate students (this introduction in the latter case is important for remedying the weakness of geometry in the usual undergraduate curriculum). In the last couple of decades differential geometry, along with other branches of mathematics, has been highly developed. In this book we will study only the traditional topics, namely, curves and surfaces in a three-dimensional Euclidean space E3. Unlike most classical books on the subject, however, more attention is paid here to the relationships between local and global properties, as opposed to local properties only. Although we restrict our attention to curves and surfaces in E3, most global theorems for curves and surfaces in this book can be extended to either higher dimensional spaces or more general curves and surfaces or both. Moreover, geometric interpretations are given along with analytic expressions. This will enable students to make use of geometric intuition, which is a precious tool for studying geometry and related problems; such a tool is seldom encountered in other branches of mathematics.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1981Количество страниц: 361Добавлена в каталог: 17.02.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Group, general linear 47 Group, of isometrics 56 Group, orthogonal 48 Hausdorff space 11 Height function 145 Heine — Borel theorem 11 132 Helicoid 181 Helicoid, as ruled minimal surface 223 Helix 79 87 96 Helix, axis of 79 Helix, circular 95 104 Helix, cylindrical 97 107 Helix, pitch of 79 Hilbert’s Theorem 249 Homeomorphic spaces 6 Homeomorphism 6 Homotopy of curves 169 Hopf — Rinow’s theorem 295 Hopf — Voss symmetry theorem 284 Hopf — Voss translation theorem 280 Hypcrbolic paraboloid 169 223 Hyperboloid, of one sheet 223 Hyperboloid, ot two sheets 157 244 Identity, Lagrange 26 Index, of vector field 264—267 Index, rotation 111 131 134 135 136 Indicatrix, binormal 97 Indicatrix, principal normal 262 263 Indicatrix, tangent 97 140 Inequality, isoperimetric 118 Infimum 9 Inner product 24 31 Integrability condition 212 269 Interior point 3 Interior, of closed plane curve 110 Interior, of set 3 Intermediate value theorem of Bolzano 14 Intrinsic property 226 Inverse function theorem 44 inversion 203 Involute 98 138 Isometric affine transformation 56 Isometry, local 198 246 Isometry, of 54 Isometry, of surfaces 197 Isometry, orientation-preserving 61 105 127 Isometry, orientation-reversing 61 Isoperimetric inequality 118 Isothermal coordinate system 200 222 Jacobi equation 302 Jacobi theorem 263 Jacobian matrix 42 JoachimstahVs theorem 196 Jordan curve theorem 110 Kernel 36 Knot 86 Knot, cloverleaf 86 Knot, figure-eight 86 Knot, four 86 Knot, Listing’s 86 Knot, overhand 86 Knot, polygonal 87 Knot, tame 87 Knot, trivial 86 Knot, wild 87 Kronecker delta 31 Lagrange identity 26 Lagrange multiplier 21 Least upper bound 9 Left-handed oriented frame field 60 85 Length, of curve see Arc length Length, of vector 24 Levi — Civita parallelism 225 Levi — Civita parallelism, property of 227 Liebmann's Theorem 247 Limit point 5 linear combination 27 Linear dependence 28 Linear independence 27 Linear space 24 Linear transformation 36 47 Linear transformation, kernel of 36 Linear transformation, nonsingular 47 Linear transformation, nullity of 38 Linear transformation, rank of 38 Liouville’s theorem 206 Local canonical form of curve 100 Lower bound 9 M 163 M 244 M 164 Maclaunn’s formula 18 100 Mamardi — Codazzt equations 212 Mannheim curve 98 Mapping, antipodal 246 Mapping, area-preserving 202 Mapping, conformal 198 Mapping, continuous 6 Mapping, derivative 41 Mapping, differential 41 Mapping, Gauss 176 Mapping, of class 35 Mapping, position 111 Mapping, principal normal 262 Mapping, regular 43 Mapping, tangential 111 Matrix, Jacobian 42 Matrix, orthogonal 48 Maximum, absolute 13 20 Maximum, relative (local) 18 20 Mean curvature 189 196 270 Mean curvature, vector 222 Mean value theorem, of differential calculus 15 Mean value theorem, of integral calculus, first 15 Mean value theorem, of integral calculus, generalized first 16 Mean value theorem, of integral calculus, second 16 Measure of set of lines 126 Mercator projection 201 Mercator projection, stereographic 169 200 Meridian, of sphere 154 Meridian, of surface of revolution 158 Meusnier’s theorem 177 Minding's theorem 246 Minimal surface 217 Minimal surface, as solution to variational problem 217 Minimal surface, Enneper’s 223 Minimal surface, of revolution 220 Minimal surface, ruled 223 Minimal surface, Scherk’s 223 Minimal surface, with isothermal parameters 223 Minimum, absolute 13 20 Minimum, relative (local) 18 20 Minkowski’s formulas 277 279 Minkowski’s problem 285 Minkowski’s problem, uniqueness theorem for 286 Monge parametrization 155 Motion, improper 61 Motion, proper 61 Motion, rigid 54 Multiplication wedge 67 Multiplication, exterior 67 Natural basis 28 Natural coordinate functions 2 Natural frame field on 30 Negatively oriented frame 60 85 Neighborhood 2 Neighborhood, open spherical 2 Norm of vector 24 Normal coordinates 234 Normal coordinates, first fundamental form in 236 Normal curvature 177 183 184 Normal line to curve 91 Normal plane to curve 91 Normal principal 91 Normal section 177 185 Normal vector field 243 245 Normal vector to surface 174 180 Nullity 38 Open covering 11 Open set 4 Opposite points 137 Orientable surface 242—243 Orientation, of frame 59 Orientation, of surface 241—245 Orientation-preserving (-reversing) isometry 61 105 127 Oriented curve 89 Orthogonal matrix 48 Orthogonal system of surfaces 203 Orthogonal trajectory 99 Orthogonal transformation 48 Orthonormal basis 28 Osculant of curve 101 Osculating circle 103 Osculating plane 91 101—102 104 Osculating sphere 103 Overdetermined system 225 Paraboloid 294 306 Parallel curves 99 116 Parallel curves, Steiner’s formulas for 116 Parallel translate 226 Parallel translate, existence and uniqueness of 226 Parallel translate, geometric interpretation of 227 Parallel vector field along a curve 225 Parallel vector field along a curve, differential equalions for 226 Parallel vector field along a curve, path-independence of 228 Parallelism, Levi — Civita 225 Parallels, geodesic 232 Parallels, of colatitude 154 Parameter of curve 78 Parameters, change of, for surfaces 165 Parameters, isothermal 200 Parametric representation of plane curve 115 Parametrization of surface 151 Parametrization of surface, isothermal 200 222 Parseval's formulas 122 Period 19 86 88 Periodic function 19 Piecewise regular (smooth) curve 82 Plane, first fundamental form of 178 Plane, normal 91 Plane, osculating see Osculating plane Plane, rectifying 91 Plane, tangent 173 180 Plateau’s problem 237 Poincare half-plane 226 250—251 Poincare theorems 70 265 Point, accumulation 5 Point, antipodal 303 Point, conjugate 302—305 Point, critical 19 180 Point, elliptic 182 185 186 Point, hyperbolic 182 185 186 Point, limit 5 Point, of application 29 Point, parabolic 182 185 186 Point, planar 183 186 Point, saddle 19 Point, umbilical 184 186 190 Polar tangential coordinates 115 Position, mapping 111 Position, vector 24 Positively oriented, boundary of simple region 254 Positively oriented, frame 60 85 Positively oriented, simple closed curve 110 Positively oriented, tangent 110 Principal, curvature 184 189 Principal, direction 184 189 Principal, normal 91 Product, inner 24 31 Product, scalar 24 Product, vector 25 Projection, Mercator 201 Projection, stereographic 169 200 Pseudosphere 195 Quadratic form 21 Radius, of curvature 91 Radius, of torsion 91 Rank of linear transformation 38 Rectifiable curve 83 Rectifying plane 91 Reflection 49 61 Region, regular 253 Region, simple 254 260 Regular curve 82 Regular mapping 43 Regular value of function 155 244 Relative topology 3 Reparametrization of curve 80—81 83 Reparametrization of curve, by arc length 84 Reparametrization of curve, orientation-preserving (-reversing) 84 Riemann symbols 213 214 Right-handed oriented frame 60 85 Rigid affine transformation 56 Rigid motion 54 Rigidity of sphere 249 Rodriques, equation of 192 Rotation index 111 131 134 135 136 Rotation, of 49 61 Ruled surface 214 Ruled surface, directrix of 214 Ruled surface, ruling of 214 Saddle point 19 Saddle surface 223 Scalar product 24 Schur’s theorem for curves 147 Screw surface 203 Second fundamental form 175 177 269 Second fundamental form, coefficients of 178 Second variation of length 302 Section, normal 177 185 Sectionally regular (smooth) curve 82 See also Positively oriented Orthogonal grou 48 Sequence, Cauchy 10 Sequence, convergent 10 Sequence, divergent 10 Set, bounded 9 Set, closed 4 Set, empty 4 Set, open 4 Sign of isometry 60 Simple curve 85 Simple region 254 260 Simple surface 155 Singular point of curve 82 Space, compact 11 Space, connected 7 Space, disconnected 7 Space, Hausdorff 11 Space, linear 24 Spaces, homeomorphic 6 Sphere, first fundamental form of 179 Sphere, meridian of 154 Sphere, parametrizations of 152—155 169 Stationary integral 75 Steiner’s formulas for parallel curves 116 Stereographic projection 169 200 Straight line 78 92 Straight line, length-minimizing property of 87 Structural equations for forms 75 269 Subcovering 11
Реклама
 |
|
О проекте
|
|
О проекте



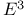
 bius band
bius band