Number of torsion points of bounded degree on an abelian variety 44
Order of a ring of integers 191
Order of a ring of integers conductor of an order 191
P(n), the greatest prime factor of n 105Ч106
p-adic methods 60 67
p-adic methods ChabautyТs theorem 58Ч60
Partition of unity 84
Pell Ч Fermat equation 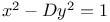 4 94 136 4 94 136
Picard group Pic(X) 2 20Ч22 34Ч36 157
Picard group Pic(X), Pic∞(X) 25 31
Poincare divisor class 37 76 78
Poincare upper half plane 67Ч68 71
Pontrjagin dual 164
Prime number theorem 181
Principal homogeneous space 100
Product formula, for a family of absolute values 7-10 22
Product formula, for a family of absolute values function fields 7Ч8
Product formula, for a family of absolute values number fields 7Ч10 113
Profinite group 147Ч149
Profinite group Frattini subgroup 148Ч149
Puiseux expansion 130Ч131 198
Pure transcendental extension 147 154 159
Quadratic functors on projective varieties 34
Quadraticity of heights on abelian varieties 35Ч39 42
Quadraticity of heights on abelian varieties on elliptic curves 40Ч41
Quasi-integral set of points 4Ч6 94
Rank of Mordell Ч Weil group 3 52 63 66 69 80 152 154Ч162
Rank of Mordell Ч Weil group elliptic curves over 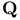 of large rank 154Ч162 of large rank 154Ч162
Rank of Mordell Ч Weil group HondaТs conjecture 162
Rank of Mordell Ч Weil group is effectively bounded 52
Regular field extension 137
Restriction of scalars functor 128
Riemann hypothesis 188
Riemann Ч Roch theorem 74 109
RiemannТs existence theorem 141
S-integers 102Ч105 112 134Ч136 141
S-units 103 112
SchanuelТs theorem 17Ч19 27Ч28 132 178
SelbergТs bound, for the large sieve 171Ч172
Sextic resolvent 125
ShihТs theorem 146Ч147
SiegelТs theorem 4Ч5 94Ч95 101Ч105 116 134 136 163
SiegelТs theorem application to curves of genus 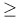 1 101Ч102 1 101Ч102
SiegelТs theorem application to P(f(n)) 105Ч106
| SiegelТs theorem approximation theorem on an abelian variety 98Ч101
SiegelТs theorem effectivity 5 100Ч101 106Ч107 116
SiegelТs theorem exceptional curve see УExceptional curveФ
SiegelТs theorem the case of curves of genus 0 102Ч104
SiegelТs theorem Thue Ч Siegel Ч Roth theorem 4 95Ч100 104Ч105 107
Sieve, the large 5Ч6 163Ч176
Sigma function of Weierstrass 91
SilvermanТs theorem 154
Specialisation of Galois groups 122Ч126 137Ч138
Specialisation of Mordell Ч Weil groups, NeronТs theorem 59 152Ч154
StarkТs conjectures 199
Strongly continuous functions 83
Superelliptic curve 117
SwanТs example 147
Sylow subgroup 124 147Ч148
Tate curve 91
Tate module of an abelian variety 70 119
TateТs normalisation lemma 29Ч30
TateТs recipe for local heights 91Ч93
Tauberian theorem 44 183
Theta functions (and local heights) 88Ч89 91
Thin set of points 121 (see also УHilbertТs irreducibility theoremФ)
Thin set of points CohenТs theorem 6 177Ч178
Thin set of points extension of ground field 128Ч129
Thin set of points in 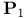 , upper bounds 5Ч6 132Ч136 , upper bounds 5Ч6 132Ч136
Thin set of points in 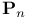 , upper bounds 6 177Ч178 , upper bounds 6 177Ч178
Thin set of points intersected with plane sections 127Ч128
Thin set of points of type 1 121
Thin set of points of type 2 121
Thin set of points polynomial interpretation 122
Thin set of points reduction modulo p of a thin set 179Ч180 183Ч186
Thue Ч Siegel Ч Roth theorem 4 95Ч100 104Ч105 107
Thue Ч Siegel Ч Roth theorem approximation of real numbers 95Ч97
Thue Ч Siegel Ч Roth theorem for function fields 105
ThueТs equation 114
Torsion points of bounded degree on an abelian variety 44
Torsion subgroup, of the Mordell Ч Weil group 43Ч44 53Ч54 68
Torsion subgroup, of the Mordell Ч Weil group number of torsion points 44 69
Weak Mordell Ч Weil theorem 3 51Ч52 99
Weak Mordell Ч Weil theorem explicit form 55Ч57
Weak Mordell Ч Weil theorem non-abelian generalisation 52
Weak Mordell Ч Weil theorem via Galois cohomology 51Ч52
Weierstrass embedding of an elliptic curve 40 57 90 115 119 155
X(N) 118 193
|
 |
|
ќ проекте
|
|
ќ проекте



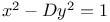
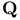 of large rank
of large rank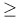 1
1 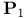 , upper bounds
, upper bounds 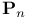 , upper bounds
, upper bounds