|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Serre J.-P. — Lectures on the Mordell-Weil Theorem |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
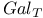 138 138
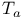 , translation on an abelian variety 38 , translation on an abelian variety 38
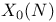 67—70 67—70
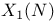 119—120 119—120
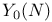 67 67
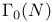 68 68
 , theta divisor 74 , theta divisor 74
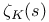 , zeta function of a number field K 182 188 , zeta function of a number field K 182 188
abc conjecture 196
Abelian variety 2 31
Abelian variety elliptic curve see “Elliptic curve”
Abelian variety generalised Mordell conjecture 73—74
Abelian variety Manin — Demjanenko theorem see “Manin — Demjanenko theorem”
Abelian variety Manin — Mumford conjecture 73—74
Abelian variety Mordell — Weil theorem see “Mordell — Weil theorem”
Abelian variety normalised heights see “Height normalised”
Abelian variety Poincare divisor 37 76 78
Abelian variety points of bounded height 53—55
Abelian variety torsion points 43—44 53—54 69
Abelian variety, approximation theorem on abelian varieties 4 95 98—101
Abelian variety, dual abelian variety 36—39 45
Abhyankar’s lemma 116
Absolute values, satisfying a product formula 7—10
Albanese variety Alb(X) 45 62
Antisymmetric divisor class 32
Approachable to within 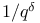 96 96
Approximation of real numbers 95—97
Approximation theorem on an abelian variety 98—101
Approximation theorem on an abelian variety effectivity 99—101 106—107
Approximation theorem on an abelian variety Thue — Siegel — Roth theorem see “Thue — Siegel — Roth theorem”
Artin — Schreier polynomial 105
Baire’s category theorem 61
Baker’s lower bounds for linear forms in logarithms 5 93 100 110—112 189 194 198—199
Baker’s method 5 94 97 108—120
Baker’s method effectivity 5 111 114 115 117
Baker’s method elliptic curves with good reduction outside a given set of places 118—120
Baker’s method on 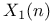 119—120 119—120
Baker’s method on 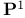 - - 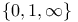 112—114 112—114
Baker’s method on elliptic curves 115 117
Baker’s method on hyperelliptic curves 115—116
Baker’s method on superelliptic curves 117
Baker’s method on Thue curves 114
Baker’s method on X(2) 118
Banach space 29 88
Belyi — Fried — Matzat — Thompson theorem 150
Belyi’s theorem 70—73
Bertini’s theorem 127 130
Birch Swinnerton — Dyer conjecture 189
Blowing up 26—27 157
Bombieri — Davenport large sieve constant 172
Bounded sets of points 81—83
Brauer group 100
Cartan subgroup 194
Cartan subgroup split and non-split 194
Cartan subgroup, normaliser of 194
Cartier divisor 83
Catalan equation 117
Chabauty’s theorem 3 58—62
Chebotarev density theorem 61
Chevalley — Weil theorem 3 50 51 109
Class number of imaginary quadratic fields 188—199
Class number of imaginary quadratic fields, class number 1 188—199
Class number of imaginary quadratic fields, class number 2 199
Classification of finite simple groups 151
Cohen’s theorem 6 177
Complex multiplication see “Elliptic curve”
Cube, theorem of the 32 34 38 77
Cubic resolvent 124
Curves Chabauty’s theorem see “Chabauty’s theorem”
Curves elliptic see “Elliptic curve”
Curves exceptional (Siegel’s theorem) 94—95 110
Curves hyperelliptic 115—116 142
Curves Mordell’s conjecture see “Mordell’s conjecture”
Curves Mumford’s inequality see “Mumford’s inequality”
Curves Mumford’s theorem see “Mumford’s theorem”
Curves superelliptic 117
Curves Tate 91
Curves Thue 114
Cusps, on modular curves 68 71 73 118
Davenport — Halberstam theorem 166—172
Demjanenko — Manin theorem 3 58 62—67
Descent lemma 3 53
Differential form 59 68 90
Dirac  -function 166 -function 166
Dirichlet series 44 181 182
Divisor, on a variety 21
Divisor, on a variety algebraically equivalent to zero 25—26 44—45
Divisor, on a variety ample 22
Divisor, on a variety class group 21
Divisor, on a variety height associated to a 2 22—24
Divisor, on a variety Poincare divisor class 37 76
Divisor, on a variety symmetric and antisymmetric divisor classes 32
Divisor, on a variety,  -divisor, on a jacobian 74 -divisor, on a jacobian 74
Divisor, on a variety, support of 21
Effectivity effective construction of an elliptic curve 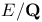 of rank of rank 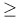 9 155—156 9 155—156
Effectivity of Baker’s method 5 111 114 115 117
Effectivity of Chabauty’s theorem 60
Effectivity of Siegel’s theorem 5 100—101 106—107 116
Effectivity of the approximation theorem on an abelian variety 99—101
Effectivity of the Manin — Demjanenko theorem 63
Effectivity of the Mordell — Weil theorem 52 99—100 107
Elliptic curve complex multiplication 44 70 93 119 191—194 196
Elliptic curve conductor 119
Elliptic curve explicit form of Mordell — Weil theorem 56—57
Elliptic curve integral points 97 115 117
Elliptic curve j-invariant 67 118 145—147 158 162 191—193
Elliptic curve local heights 90—93
Elliptic curve normalised heights 40—41 90—93
Elliptic curve of large rank over 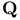 121 154—162 121 154—162
Elliptic curve Tate module 70 119
Elliptic curve torsion points 69
Elliptic curve with good reduction outside a finite set of places 118—120
Embedding a field finitely generated over 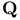 in in 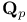 61—62 61—62
Exceptional curve (Siegel’s theorem) 94—95 110
Exceptional units 104
Fermat curve 110
Fermat quartics (Demjanenko’s theorem) 66—67
Function fields 7—8 19
Function fields heights 11—13
Function fields number of points of bounded height in 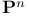 19 19
Functions of degree 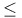 2 between abelian groups 32—34 38 2 between abelian groups 32—34 38
Fundamental group 141 150
Galois cohomology 51—52
Galois group 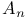 144—145 144—145
Galois group 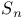 138—144 145 138—144 145
Galois group Belyi — Fried — Matzat — Thompson theorem 150
Galois group finite simple 151
Galois group infinite 147—149
Galois group Noether’s method 147
Galois group Schur’s examples 145
Galois group Shih’s theorem 146—147
Galois group using elliptic curves : 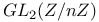 , , 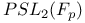 , , 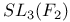 145—147 145—147
Galois group with rigid family of rational conjugacy classes 149—150
Galois group, construction of field extensions of 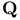 with given 6 121 with given 6 121
Gel’fond — Linnik — Baker method 197—199
Generalised Riemann Hypothesis (GRH) 188
Goldfeld’s theorem 189
Grassmannian 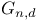 127 127
Greenberg’s theorem 83
Gross — Zagier theorem 188 189
Grothendieck — Deligne (Weil conjectures) 184
Hasse’s theorem 156
Height associated to a divisor algebraically equivalent to zero 25—26 44—45
Height associated to a line bundle 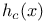 2 22—28 2 22—28
Height associated to a morphism 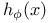 19—20 19—20
Height associated to a Poincare divisor 36—39
Height associated to a torsion divisor 24 46—48
Height behaviour under change of coordinates 13
Height bilinear form 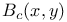 associated to associated to 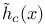 36 41 36 41
Height change of height under projection 13—16 19—20
| Height elementary properties 10—16
Height for function fields 11—13
Height for number fields 11
Height logarithmic height h(x) 2 11
Height non-degeneracy of normalised heights 41—43
Height normalised height 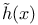 , , 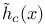 2 30—31 35—43 63 134 2 30—31 35—43 63 134
Height Northcott’s finiteness theorem 16—17
Height of a rational point H(x) 2—6
Height on 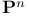 10—13 10—13
Height positivity 24—25
Height quadraticity of normalised heights on abelian varieties 35—41
Height relation between quadratic and linear parts of 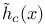 38—39 38—39
Height Schanuel’s theorem 17—19
Height, functoriality of 23
Height, local height see “Local heights”
Hensel’s Lemma 62
Hermite’s finiteness theorem 3 49—52 109
Hermitian structure on a line bundle 84—85
Hilbertian field 129—130 137—138
Hilbertian field, finitely generated extensions of hilbertian fields are hilbertian 130
Hilbert’s irreducibility theorem 5—6 121 130 149
Hilbert’s irreducibility theorem 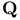 is hilbertian 130—132 is hilbertian 130—132
Hilbert’s irreducibility theorem Neron’s specialisation theorem see “Neron’s specialisation theorem”
Hilbert’s irreducibility theorem relation with integral points 135
Hilbert’s irreducibility theorem specialisation of Galois groups 122—126 137—138
Hilbert’s irreducibility theorem thin sets see “Thin sets”
Hilbert’s irreducibility theorem, hilbertian field 129—130 137—138
Honda’s conjecture 162
Hurwitz’ genus formula 142—143
Hyperelliptic curve 115—116
Inertia subgroup 140 143 150
Integral points 4—6 94—95 97 100 102—106
Integral points Baker’s method 5 94 97 108—120
Integral points behaviour under morphisms 108—110 114
Integral points elliptic curves with good reduction outside a finite set of places 118—120
Integral points exceptional curves 94—95 110
Integral points of bounded height 6 115 117 177—178
Integral points on 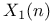 119—120 119—120
Integral points on 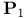 - - 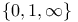 5 102—104 112—114 5 102—104 112—114
Integral points on elliptic curves 97 115 117
Integral points on hyperelliptic curves 5 115—116
Integral points on modular curves and the class number 1 problem 194—199
Integral points on superelliptic curves 117
Integral points on Thue curves 114
Integral points on X(2) 118
Integral points quasi-integral sets 94—95
Integral points S-integral points 94 104—105
Integral points Siegel’s theorem (see also “Siegel’s theorem”) 95 102—104
Intersection multiplicities 85—86
Jacobian of a curve 1—2 5 46 58—59 66 73 98 101 134
Jacobian of a curve  divisor 74 divisor 74
Jacobian of a curve is principally polarised 46 76
Jacobian of a curve Poincare divisor class 76
Kissing number 79
Kronecker’s limit formula 194 199
Kubert — Lang 115 119—120 197
Kummer theory 55—56
L-function 188 189 198—199
Lang — Weil theorem 6 62 184
Large point 79 80
Large sieve inequality 6 163—164
Large sieve inequality Bombieri — Davenport bound 172
Large sieve inequality Davenport — Halberstam theorem 166—172
Large sieve inequality improved inequalities 170—172
Large sieve inequality Selberg’s bound 171—172
Legendre’s equation of an elliptic curve 118
Lenstra’s example 147
Lie group 60 149
Line bundle, generalities 20—22
Line bundle, generalities ample 22
Line bundle, generalities generated by its global sections 21—22
Line bundle, generalities the Picard group Pic(X) 20—22
Linear torus 73
Local heights 83—93
Local heights as intersection multipicities 85—86
Local heights case of an abelian variety with good reduction 89
Local heights in terms of theta functions 88—89
Local heights normalisation on abelian varieties 87—89
Local heights relation with global heights 89—90
Local heights Tate normalisation on elliptic curves 90—93
Locally compact field 81
Logarithmic height 2 11
Lower bounds for linear forms in logarithms 5 94 110—112
Manin — Demjanenko theorem 58 62—66 154
Manin — Demjanenko theorem application to Fermat quartics 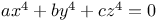 66—67 66—67
Manin — Demjanenko theorem application to modular curves 67—69
Manin — Demjanenko theorem application to the Tate module of an elliptic curve 73—74
Manin — Drinfeld theorem 73 197
Manin — Mumford conjecture 76
Mazur’s theorem 69
Modular curves 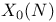 67—70 146 67—70 146
Modular curves 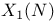 119—120 119—120
Modular curves 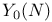 67 67
Modular curves associated to Cartan subgroups and their normalisers 194—197
Modular curves Belyi’s theorem 70—73
Modular curves cusps 69 71 73 118 195—197
Modular curves Manin — Drinfeld theorem 73
Modular curves Manin’s theorem 67—69
Modular curves X(N) 118 193
Mordell — Weil theorem 1 3—4 52 58 99 100
Mordell — Weil theorem classical descent 53
Mordell — Weil theorem effectivity 52 99—101 107
Mordell — Weil theorem explicit form 55—57
Mordell — Weil theorem for finitely generated ground fields 52
Mordell — Weil theorem weak Mordell — Weil theorem 3 51—52 99
Mordell-Weil group 43—44 51—53
Mordell-Weil group rank 3 58—59 69
Mordell-Weil group torsion subgroup 43—44 54 69
Mordell-Weil group, generators for 99
Mordell’s conjecture 1 3—4 58—59 105 133
Mordell’s conjecture Chabauty’s theorem see “Chabauty’s theorem”
Mordell’s conjecture generalised 73—74
Mordell’s conjecture in characteristic p > 0 80 105
Mordell’s conjecture Manin — Demjanenko theorem see “Manin — Demjanenko theorem”
Mordell’s conjecture Manin — Mumford conjecture see “Manin — Mumford conjecture”
Mordell’s conjecture Mumford’s theorem see “Mumford’s theorem”
Multiplicative function 182
Mumford’s inequality 77
Mumford’s lemma 23
Mumford’s theorem 3—4 58 74—80 105 133
Mumford’s theorem optimal for function fields 80
Nakai — Moishezon criterion 26 27
Neron model of an abelian variety 89
Neron — Severi group NS(X) 25 31—32 47 62 64 157
Neron — Tate normalisation 2 29—31 35
Neron’s estimate 53—55
Neron’s normalisation of local heights 87—89
Neron’s specialisation theorem for abelian varieties 59 152—154
Neron’s specialisation theorem for abelian varieties Silverman’s theorem 154
Neron’s specialisation theorem for abelian varieties specialisation of extensions of abelian varieties 154
Neron’s specialisation theorem for abelian varieties specialisation of non-commutative groups 154
Noether’s method 147
Non-degeneracy of normalised heights 42—43 (see also “Height” “
Normalised heights 2 30—31 34—48
Normalised heights non-degeneracy 42—44
Normalised heights on elliptic curves 39—41
Normalised heights positivity 41
Normalised heights quadraticity 35—36
Normalised heights, normalised local heights 87—89 90—93
Northcott’s finiteness theorem 16—17 44 46 53
Northcott’s finiteness theorem quantitative form (Schanuel’s theorem) 17—19 132
NS(X), Neron — Severi group 26 31—32 47 62 64 157
Number of integral points of bounded height on a thin set 6 134—136 163 177
Number of integral points of bounded height on an affine variety 177—178
Number of rational points of bounded height on 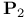 blown up at a point 26—28 blown up at a point 26—28
Number of rational points of bounded height on 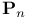 2 17—19 2 17—19
Number of rational points of bounded height on a curve 5—6 80
Number of rational points of bounded height on a thin set 5—6 132—134 178
Number of rational points of bounded height on an abelian variety 53—55
Number of rational points of bounded height on an algebraic variety 178
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



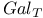
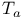 , translation on an abelian variety
, translation on an abelian variety 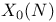
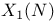
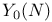
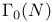
 , theta divisor
, theta divisor 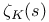 , zeta function of a number field K
, zeta function of a number field K 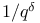
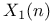
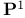 -
- 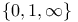
 -function
-function 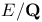 of rank
of rank 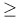 9
9 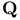
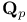
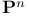
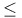 2 between abelian groups
2 between abelian groups 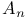
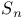
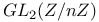 ,
, 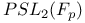 ,
, 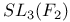
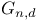
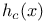
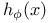
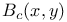 associated to
associated to 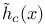
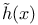 ,
, 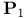 -
- 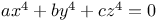
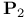 blown up at a point
blown up at a point