|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Deligne P., Kazhdan D., Etingof P. — Quantum fields and strings: A course for mathematicians (Vol. 1) |
|
|
 |
| Предметный указатель |
 -function 10 568 574 583 779 1163 1292 1306 1368 1379 1390 1433 1451ff -function 10 568 574 583 779 1163 1292 1306 1368 1379 1390 1433 1451ff
 -runction 779 783 -runction 779 783
 -model 7 211ff 263ff 279ff 437 492ff 773ff 895 1171ff 1183ff 1292ff 1313ff -model 7 211ff 263ff 279ff 437 492ff 773ff 895 1171ff 1183ff 1292ff 1313ff
 -model, twisted 802 1324 -model, twisted 802 1324
 -dependence 1213 -dependence 1213
 -term 7 306 210 223 326 335 1252 see -term 7 306 210 223 326 335 1252 see
 -runction regularization 185ff 483 673 678 737 855ff -runction regularization 185ff 483 673 678 737 855ff
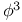 -theory 423 435 621 782 -theory 423 435 621 782
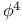 -theory 440 444 456 571 576 626 629 -theory 440 444 456 571 576 626 629
't Hooft loop 36 1255ff
1-loop 570 577 625 783ff 868 971ff 975ff 1308ff
1-particle irreducible 429
1-particle irreducible, correlation Function 704
1-particle irreducible, effective action 773
1-particle irreducible, graphs 1187
action 7 143 729 817 see
Action, effective see “Effective action”
Amdiiary variable 237 1095
Anftatz 8
Anomaly 8 740 885 901 1166ff 1297 1432 1447ff 1463 1464 1489
Anticfairal 252
Antiinstanton 1213 1236
asymptotic freedom 8 469ff 570 788 1440
Asymptotically free theory 576 1151 1348
Background (field) 9 780 9038
Bare, coupling 592 780
Bare, mass 430 644
Beltrami, differential 852ff
Beresin integral 483 744
Beretmian 59ff 83 612 619
beta function see “ -function” -function”
Bethe anaats 800
Born aitproadmation 464
Bose field 10 236
Bose — Fexmi comspoD fence 1199ff 1205ff
Boson 10
Boson, Goldstone 187 1139 1142ff 1342 1344 1411
BPS (state) 9 1283ff 1370ff
BPS (state), classical 9 1281ff
BPS (state), formalism 1358f
BPS (state), monopole 1289
BRST 9 878ff 1061ff
BRST, charge 961
BRST, cohomology 880 1162ff
BRST, current 961
BRST, differential 879 1161 1162
BRST, quantization 871ff 961ff 1159ff
Calabi — Yau manifod 740 789 912 11058 1292 1305 1333
Cartan model 1264ff
Central'charge see “Charge central”
Chan — Paton rules 841ff 937
Charge, central 11 858 10436" 1295 1359
Charge, density 202 541
Charge, Noether see “Noether charge”
Chera — Simon term 216 612 660 1233
Chiral 11
Chiral, algebra 1025ff 1045 1049ff 1067ff 1082ff
Chiral, operator 1488 1492
Chiral, ring 1334ff 1453
Chiral, superadd 252 259 635 1417
Chiral, symmetry 1200
Classical, field 11 155ff
Classical, limit 12
Classical, solutions 161
Classical, vacuum 183ff
Clifford modules 107ff 232
Coleman — Mandiila theorem 1176 1176
COLOR 1432
Compactification 12 738ff 1098 1106
Component field 34 236S
Composite operator 448 452 455 576
confinement 12 1195 1220ff 1258ff 1271 1345 1433 1448
Conformal blocks 1031ff 1084ff
Conformally invariant (confornal) field theory 459 727ff 824ff 874ff 1017ff 1203
Conserved current 12 176 825 1154
Convergence, superficial 432
Correlation function 12 447 453 741 1031ff 1131 1318
Correlation function, (n-point) 421 731
Coulomb, phase 13 1260
Coulomb, potential 1194 1236
Counterterm 13 430 441 442 569
Coupling 13 436 784
CPT 392ff
Critical, coupling 1163
Critical, dimension 437
Critical, field tbeoiy 440 452
Current 13 162 1201
Cutoff 13 560 1173
Cutoff function (cutoff propagator) 441 455 557
D-modules 1020ff
Debye screening 1237
Deligne cohomology 218ff
Dilatino 933 1101 1105
Dilaton 1052
DIMENSION 153
Dimension, of a field 451
Dimension, of an operator 14
Dimension, of an operator, anomalous 14 580ff 629 1415
Dimension, of an operator, engineering 14 446 567
Dimension, of an operator, quantum 14 451
Dimension, scaling 14 446
Dimensional, reduction 14 187ff 245ff 276ff 291ff 331
Dimensional, regularizaiion 560 564 566 597ff 673 781ff 897
Dimensional, transmutation 592 1433
Dirac fermions (Dirac tpinors) 32 744
Dirac operator 196 235 477ff 489ff 497ff 614 628 891 1100
Divergence (logarithmic, linear, quadratic, superficial) 429 431 436 443 786 1173
Donaldson theory 645 1392ff
Duality 14 1225ff 1456 1488
Dynkin diagram 101
Dytiamical, mass generation 585ff
Dytiamical, symmetry breaking 585ff
Dytiamical, variable 15
Effective, action 15 777ff 908ff 1097 1101 1101ff 1187 S241415
Effective, coupling 564 566
Effective, cross-sectional area 463
Effective, lagrangian 15 556 1112 1161 1207 1423
Effective, potential 15 1123 1429 1442 1444 1446
Effective, theory 15 586 1186ff 1394ff
Electric charge 15 209
Electromagnetic duality 1240 1354ff 1454ff
electromagnetic field 145 201ff 540 1193
Electron 16
Elementary field see “Field elementary”
Elliptic curve 744 1368 1376 1376ff 1483
Elliptic genus 1330
Energy-momentum tensor 16 176ff 750ff
Euclidean action 221ff see
Euler — Lagrange equations 16 537 653 657 692 1249
expectation value 16 495
Faddeev — Popov, determinant 855 873 1228
Faddeev — Popov, ghosts 871ff
Faddeev — Popov, method 16 796
Fayet — Hiopoulo B term 308
Fermi field 10 236
Fermion 10 744 943 947 1199 1202 1447
Fermion, Goldstone 633
Feynman — Kac formula 672 732 791 1128
Feynman, diagrams (graphs) 17 426 465 561 589 605 674 682 685ff 701 814 865ff 978ff 1187ff
Feynman, diagrams (graphs), amphtude 865ff
Feynman, famous formula 427
Feynman, integral 424ff 597ff 729
Field 17
Field, auxiliary see “Auxiliary variable”
Field, background see “Background field”
Field, classical see “Classical field”
Field, component see “Component field”
Field, elementary 11 16
Field, local see “Local field”
Field, strength 17
| Flavor 1341 1434 1439ff
Fock space 18 503 527 745 631ff 876ff 919
Free, classical electrodynamics 198ff 201ff 396
Free, Classical field theory 191ff 395 539
Free, QFT of arbitrary spin 398
Free, quantum field tltcon 18 449 523ff 1205
Free, scalar QFT 192 397 526ff
Free, spinor QFT 195 398
Functional determinant 855 884 891
Galilean group 151
Gauge 18 837
Gauge, boson 18
Gauge, field 18
Gauge, fixing 1096
Gauge, group 18
Gauge, theory 201ff 438 1191
Gauge, theory, abelian 198ff 201ff 1209ff
Gauge, theory, nonabelian 1432ff
Gauge, transformation 10 793
Gauging a symmetry 19 175ff 1152
Gaugino 1101 1105
Gaussian, integral 19 731 1423
Gaussian, measure 402
Ghort 19 833ff 1163
Ghost number 1164
Gluon 20 1445
Goldstone boson see “Boson Goldstone”
Goldstone fermion see “Fermion Goldstone”
Goldstone theorem 1136
Grassmaniann variables 41ff
Grassmannian 1071ff 1183ff
Gravitational field 20 156 180ff 542
Gravitino 920 933 1101 1105
Graviton 840
Gravity 542ff
Green's function 891
Gross — Neveu model 587ff
GSO projection 927ff 945
Haag — Ruelle scattering thaory 407ff
Hamiltonian 20 172 480 537ff
Hamiltonian, formalism 20 163ff 486 537ff
harmonic oscillator 487 520 523ff 620 622 733
Heisenberg algebra 1049ff
Helicity 20
Heterotic string 941ff 110ff
Higgs mechanism 20 185ff 645 1232 1259
Higgs phase (regime) 1218ff 1260
Higher derivative term 20
Hypermuttiplet 1374 1387 1396
Imaginary time 221 891
Index of elliptic operator 475ff 691 695
Instanton 21 1210 1212 1235 1440
Instanton, gas 1211 1236
Integral, density 154 239
Integral, form 84ff 154
Integrating out 21 922 1232
Interaction 21 452 456
IR (infrared) 1331
IR (infrared), behavior 1141 1171ff 1209 1343 1489
IR (infrared), limit 21 1155
IR (infrared), stable fixed point 1344
Jost'a theorem 387
Kac — Moody algebra 739 1049ff
Kalosa — Kletn I095ff
Kinetic term 21
Klein — Gordon, equation 526
Klein — Gordon, popagator 422
Lagrangian 21 162ff 198 611ff 1206 1226 1341 1345 1348 1353 1362 1363
Lagrangian, denity 21 143 157ff 237ff 696 1127 1132
Lagrangian, effective see “Effective lagrangian”
Lagrangian, formalism 21 537ff
Landau singularity 374
Landau — Ginzburg 1300 1327ff
Large N limit 22 388ff 1171ff 1183ff 1404 1405
Lehhmann — Symanzik — Zimmermann (LSZ) formalism 864
Lightcone 12
Lightcone, gauge 22 837 986
LIMIT see “Classical limit
Lippmann — Schwinger equation 463
Little group 22
Local, field 156
Local, functional 445ff
Local, operator 1336
Local, symplectic form 368
localization 1267
Loop, group 792
Loop, space 497ff
Lorentz, invariance 547
Lorentz, metric 358
Low energy 23
Low energy, behavior 23 1352ff
Low energy, effective Lagrangian 23
Low energy, effective theory 23
Low energy, limit 23
Magnetic, charge 23 209
Magnetic, theory 1454
Majorana spinor 32 929
Majorana — Weyl spinor 929 1101 1105 1108
Manifest symmetry 169
Marginal, interaction 1171
Marginal, perturbations 1294
Mass 23
Mass, gap 1202 1342 1345 1348 1433 1437
Mass, spectrum 383
Massless, scalar 735
Massless, spinor 744
Maxwell theory 23 201ff 540ff 1225
Minimal, coupling 19
Minimal, subtraction 782ff 787ff
Minkowski space 23 150 191 358
Modular form 1242
Moduli space of vacua 24 38
Moduli space of vacua, classical 24 185 304ff 1349 1302 1428 1434ff 1463 1467 1469
Moduli space of vacua, quantum 24 1366ff 1429 1436ff 1445 1469 1470 1476
Moment map 147 1268 1421
Momentum 24 148
Momentum, transfer 464
monopole 24
Neveu — Schwarz sector 24 745 918ff
Noether, charge 25 147ff 170 359
Noether, current 25 147ff 170 175 193 362
Noether, theorem 147 165ff 825
Nonlinear  -model 211ff 267ff 895ff -model 211ff 267ff 895ff
Nonperturbative effect, result 25
Nonrenormalizable field theory 558 1141
Normal ordering 402 448 452
Observable 25 515
Octonions 133ff
Off-shell 25 161
On-shell 25 161
One-loop see “1-Ioop”
Operator 26 see operator”
Operator product expansion (OPE) 25 449ff 456ff 794 825 964 1453
Operator, composite see “Composite operator”
Orbifolding 1301
Particle, quantum 26
Particle, relativistic 26
Partition function 27 1186 1227 1241 1270ff
path integral 27 481ff 505ff 623 624 681 691ff 1172 1218ff 1227 1231 1256
Pauli — Villars regulator fields 1168
Perturbation expansion 27 185 421ff 424ff
Perturbation theory 27 524ff 955ff 1440
Phase shift 462
Phase transition 559
Photon 28 540
Planck length 1096
Poincare, algebra 28 359
Poincare, group 151 379ff 1112
Poincare, group, positive representation of 422
Poisson brackets 148 170 359 367 372
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -function
-function  -runction
-runction  -model
-model  -dependence
-dependence  -runction regularization
-runction regularization 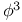 -theory
-theory 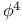 -theory
-theory