|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Griess R.L.Jr. — Twelve sporadic groups |
|
|
 |
| Предметный указатель |
"Extra automorphism" of A 97
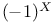 36 95 36 95
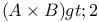 22 22
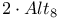 121 121
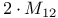 76ff 76ff
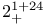 , , 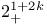 117 117
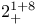 117 117
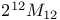 111 111
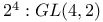 55 57 55 57
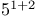 116 116
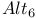 18 119 18 119
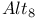 57 118 57 118
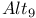 117 117
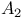 -lattice 90 -lattice 90
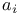 , , 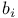 , , 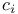 59 59
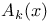 105 105
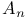 -lattice 91 -lattice 91
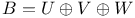 132 132
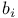 , , 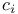 , , 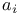 59 59
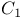 , Aut( , Aut(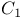 ) 31 32 ) 31 32
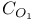 , simclicity of 101 , simclicity of 101
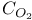 123 123
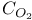 , simplicity of 108 , simplicity of 108
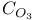 123 123
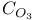 , double transitivity of 105 , double transitivity of 105
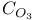 , simplicity of 105 , simplicity of 105
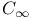 132 132
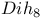 11 11
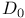 , ,  , , 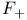 , , 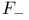 71 71
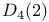 121 121
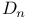 -lattice 91 -lattice 91
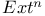 13 13
 , , 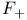 , , 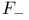 , , 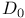 71 71
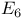 -lattice 91 -lattice 91
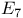 -lattice 91 -lattice 91
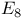 134 134
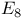 -lattice 91 -lattice 91
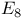 -lattice theta function 92 -lattice theta function 92
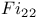 , , 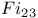 , , 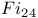 134 134
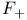 , , 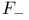 , , 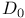 , ,  71 71
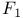 , , 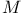 1 131 134 1 131 134
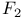 134 134
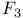 134 134
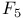 134 134
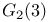 134 134
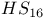 -lattice theta function 92 -lattice theta function 92
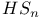 92 92
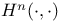 , n-th cohomology group 12 , n-th cohomology group 12
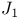 135 135
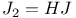 104 123 104 123
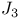 135 135
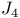 137 137
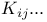 44 77 44 77
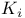 39 77 39 77
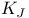 44 77 44 77
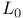 95 95
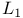 , , 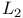 60 60
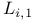 61 61
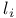 39 39
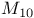 18 66 18 66
 66 75 66 75
 , , 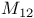 , , 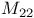 , , 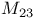 , , 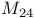 54ff 54ff
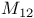 62ff 85ff 119 123 62ff 85ff 119 123
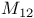 , classes of elements of order 3 87 , classes of elements of order 3 87
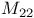 75 114ff 75 114ff
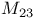 75 75
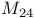 2 6 18 19 47 54ff 2 6 18 19 47 54ff
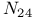 97 97
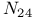 , conjugacy of involutions 110 , conjugacy of involutions 110
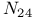 , maximality of 100 , maximality of 100
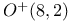 117 117
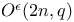 21 21
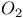 30 30
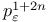 20 20
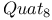 11 119 11 119
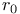 , , 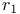 , , 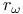 , , 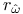 57 57
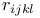 57 57
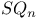 91 91
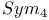 30 30
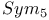 29 29
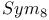 57 57
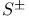 71 71
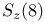 136 136
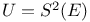 132 132
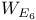 118 118
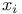 , , 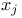 , z 113 , z 113
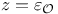 114 114
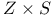 28 28
 33 117 33 117
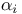 95 95
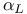 , , 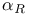 64 86 64 86
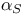 , for , for 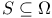 95 95
 86 117 86 117
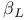 , , 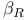 64 64
 118 118
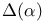 124 124
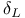 , , 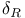 64 64
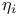 97 97
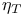 97 97
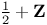 , the semiintegers 93 , the semiintegers 93
 117 117
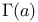 124 124
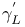 , , 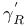 64 64
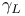 , , 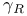 64 64
 , ,  84 84
 , the standard Leech lattice 95 , the standard Leech lattice 95
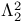 , , 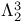 , , 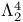 95 95
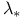 , , 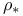 85 85
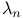 95 95
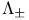 118 118
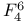 78 78
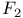 , , 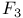 , , 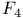 26 26
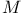 , , 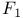 , symbols for the Monster 1 131 , symbols for the Monster 1 131
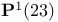 , the projective line over the field of 23 elements, , the projective line over the field of 23 elements, 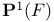 , the projective line over the field F 60 , the projective line over the field F 60
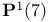 , the projective line over the field of 7 elements 59 , the projective line over the field of 7 elements 59
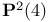 , the projective plane over the field of 4 elements 66 , the projective plane over the field of 4 elements 66
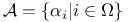 , standard basis for , standard basis for 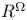 95 95
 , a common symbol for dodecad 37ff , a common symbol for dodecad 37ff
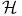 30 30
 39 39
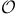 , a common symbol for an octad 36 , a common symbol for an octad 36
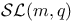 71 71
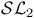 , , 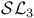 , , 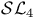 48 68 48 68
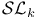 48 68 48 68
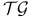 78 78
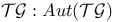 121 121
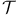 54ff 54ff
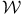 40 40
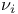 95 95
 , a primitive cube root of unity in , a primitive cube root of unity in 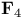 30 30
 , multiplication by 42 , multiplication by 42
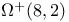 117 117
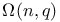 18 19 18 19
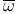 , the other primitive cube root of unity in , the other primitive cube root of unity in 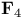 30 30
 -labeled points 82 -labeled points 82
 42 42
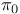 41 42 41 42
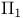 42 57 42 57
 , ,  84 84
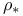 , , 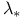 85 85
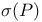 9 9
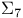 116 116
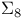 122 122
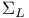 , , 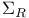 , , 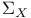 83 83
 26 64 26 64
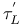 , , 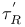 64 86 64 86
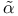 85 85
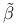 86 86
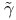 85 85
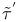 85 85
| 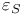 , for , for 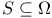 95 95
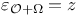 117 117
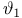 , , 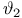 , , 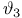 , , 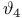 117 117
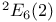 133 133
((abcd)) 78
(T) 78
.223 121
.223, simplicity of 107
.333 122
.abc, the stabilizer in Aut( ) of a triangle of type abc 101 ) of a triangle of type abc 101
2-rank 75
27th sporadic 138
4-tuple labeling 77 82
6-tuple labeling map 39
A.B, A:B, 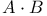 11 11
abc, triangle of type 101
Accents graves 35
Additive functor 12
AGL(2,3) 66
Alperin, Jon 15 19
Alternating groups 16
Anisotropic 25
Annihilator 90
Associated graph 124
Associated labeled set 78
Associated picture 37
Augmentation submodule 4
Aut( ) 116 ) 116
Aut( ) 84ff 117 119 ) 84ff 117 119
Aut(C), Aut*(C), for a code C 27
Aut(F) 26
Aut(L), for a lattice L 89
B 132ff
Baby Monster 133 134
Balance condition, well-balanced condition 40 78
Balance, hexacode 34
Balanced set, parity, well balanced 40 76
Benson, David 3 137
Bilinear 24 25
Bilinear function 21
BINARY 25
Binary Golay code 36
Boolean sum 24
Broue, Michel 135
Burnside Basis Theorem 8
Burnside Normal p-Complement Theorem 8
C=C(z), centralizer of the involution z 117 131ff
Central extension 14
Chevalley — Steinberg presentation 22
Choi, Chang 54
Classes of elements of order 3 in  87 87
Classes of elements of order 5 in 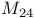 122 122
Classification of even unimodular lattices 93
Classification of finite simple groups 137
Classification theorems 125
Cocode 26 80
Code equivalence, strict equivalence 27
Code equivalence, strict equivalence, thickened codes 27
Code parameters 25
Code, linear error correcting codes, error correcting codes 25ff
Cohomology of groups 12
Column distribution 81
Commuting criterion 57
Conjugacy classes 1A, 2A, 2B, 3A, 3C, 4A, 4B, 5A, 6A 135
Conjugacy classes of elements of order 3 in Aut( ) 120 ) 120
Conjugacy of involution in 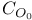 111 111
Conjugacy of involutions in 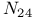 110 110
Conway groups, 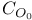 , , 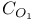 , , 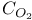 , , 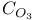 101 101
Coordinate permutations 26
Covering 14
Coxeter group 22
Curran, Peter 19
Curtis, Robert 3 54
Cycle shape 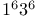 116 118 116 118
Cycle shapes 116
Darstellungsgruppe 15
Defective 24
Degenerate 24
Degree 5
Diag(n,F), 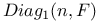 26 27 26 27
Diagonal group 26
Diagonal matrices 68
Distance 25
Dodecad 37ff
Dodecad pure subspace 70
Dodecad triangle 52
Dodecad-universe pure subspace 71
Dodecads, left and right, L, R 64 86
Dodecads: subspaces with none 75
Elements of order 3 116ff
Elliptic modular function, j 135
Equivalent codes, strict linear equivalence 27
Error correcting codes 25
Error correcting properties of tetracode 77
Essential extension 14
Even elements 6
Existence corollary 134
Extended monomial group 26
Extension 11
Extension kernel 11
Extension quotient 11
Extension theory 3
Extension, simultaneous componentwise downward 22
Extension, simultaneous componentwise upward 22
Extra automorphism 133
Extraspecial p-group 19
Feit, Walter 3 8
Field automorphism 68
Finite groups of Lie type 16
Finiteness 133
Fischer — Griess Monster 1 131ff
Fischer — Griess simple group 1 131ff
Fischer, Bernd 1 133
Formula for the number of isotropic subspaces 27
Fours group, 2A-pure 133
Foursome 81
Frame 102
Frame in 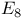 94 94
Frames fixed by 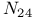 112 112
Frattini argument 5
Frattini subgroup 8
Frohardt, Daniel 136
FSX(3,4) 55 67 75 108
functor 12
G( ) 72ff ) 72ff
G(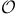 ) 55 57ff ) 55 57ff
G(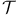 ) 55 58 ) 55 58
G(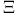 ) 55 57 ) 55 57
G(i) 59
G(X), 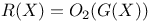 , L(X) 55 , L(X) 55
Generations 1
Genus zero 135
GL(2,112)2 137
GL(2,3) 76
GL(2,F) 60
GL(3,2) 14 137
GL(4,2) 57
GL(n,F) 9
GL(n,q) 6
Golay cocode 38
Golay code, binary Golay code, 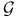 27 36ff 27 36ff
Golay code, uniqueness of 44 46
Gorenstein, Daniel 19 137 138
Gram matrix 88
Graph 124
Griess algebra 135
Griess, Robert 15
Half spin lattice, 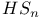 92 92
Hall — Janko group 104 123
Hamming code 27
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



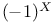
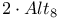
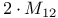
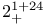 ,
, 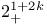
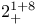
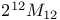
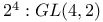
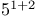
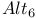
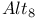
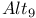
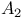 -lattice
-lattice 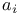 ,
, 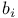 ,
, 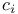
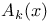
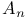 -lattice
-lattice 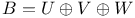
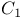 , Aut(
, Aut(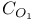 , simclicity of
, simclicity of 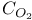
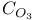
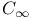
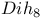
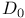 ,
,  ,
, 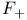 ,
, 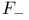
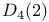
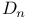 -lattice
-lattice 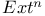
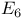 -lattice
-lattice 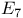 -lattice
-lattice 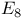
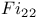 ,
, 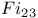 ,
, 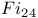
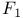 ,
, 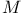
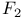
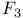
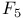
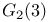
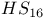 -lattice theta function
-lattice theta function 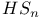
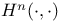 , n-th cohomology group
, n-th cohomology group 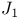
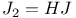
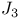
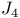
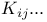
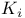
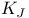
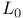
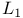 ,
, 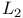
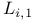
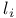
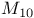

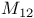 ,
, 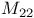 ,
, 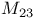 ,
, 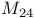
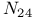
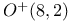
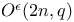
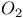
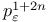
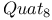
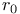 ,
, 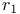 ,
, 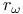 ,
, 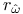
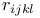
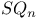
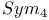
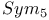
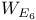
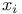 ,
, 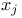 , z
, z 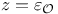
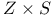

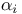
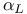 ,
, 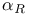
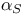 , for
, for 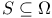

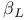 ,
, 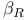

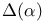
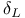 ,
, 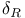
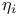
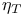
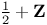 , the semiintegers
, the semiintegers 
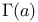
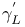 ,
, 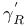
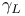 ,
, 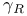
 ,
, 
 , the standard Leech lattice
, the standard Leech lattice 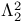 ,
, 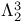 ,
, 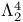
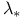 ,
, 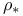
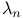
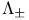
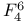
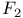 ,
, 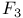 ,
, 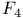
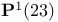 , the projective line over the field of 23 elements,
, the projective line over the field of 23 elements, 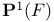 , the projective line over the field F
, the projective line over the field F 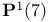 , the projective line over the field of 7 elements
, the projective line over the field of 7 elements 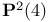 , the projective plane over the field of 4 elements
, the projective plane over the field of 4 elements  , standard basis for
, standard basis for 
 , a common symbol for dodecad
, a common symbol for dodecad 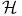

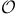 , a common symbol for an octad
, a common symbol for an octad 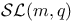
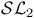 ,
, 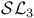 ,
, 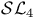
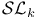
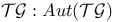
 , a primitive cube root of unity in
, a primitive cube root of unity in 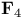
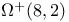
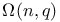
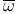 , the other primitive cube root of unity in
, the other primitive cube root of unity in  -labeled points
-labeled points 
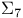
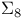
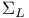 ,
, 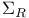 ,
, 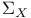

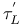 ,
, 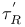
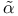
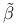
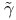
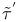
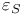 , for
, for 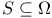
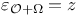
 ,
,  ,
,  ,
, 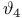
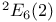
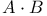
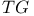 )
) 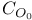
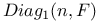
 )
) 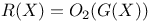 , L(X)
, L(X)