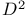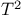|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Nash C., Sen S. Ч Topology and geometry for physicists |
|
|
 |
| ѕредметный указатель |
 -planes 285Ч289 -planes 285Ч289
 -planes and anti-self-dual connections 288Ч289 -planes and anti-self-dual connections 288Ч289
 -planes and complex projective space 287Ч288 -planes and complex projective space 287Ч288
 -planes 285Ч288 -planes 285Ч288
Affine transformation law 178 181
Algebraic geometry 289 294
Almost complex structures 170Ч171
Almost Hamiltonian structures 165Ч167 171
Anti-self-duality 259 285Ч297
Anti-self-duality and  -planes 286 288Ч289 -planes 286 288Ч289
Anti-self-duality and holomorphic structure 292Ч297
Anti-self-duality, definition of 259
Atiyah Ч Singer index theorem 220 280
Atiyah Ч Singer index theorem and instantons 280
Atlas 26 36Ч37
Betti number 91
Bianchi identities 182Ч183 190 192 257
Biholomorphic 221
Bogomolny equation 298Ч301
Bohm Ч Aharanov effect 301Ч302
Boundary 86
Boundary operator 84 121Ч123
Brouwer fixed point theorem 6
Calculus on manifolds 37Ч48
Canonical transformations 169
Cap product 139
Cauchy's residue theorem 1Ч2
Chain 84
Characteristic classes see "Names of specific characteristic classes"
Characteristic classes in general 200Ч225
Characteristic classes in terms of curvature and invariant polynomials 206Ч211
Characteristic classes of a manifold 219
Characteristic classes, calculation of 213Ч217
Characteristic classes, formulae obeyed by 219Ч221
Characteristic classes, universal 221
Characteristic numbers of a manifold 219
Chart 26 36Ч37
Chern character 220
Chern classes 204Ч210 213Ч215 217Ч220
Chern classes in terms of curvature 207Ч210
Christoffel symbol 187
Closed form 123
Closed set 13Ч15 17
Cohomology 120Ч139
Cohomology and de Rham cohomology 122Ч138
Cohomology and non-compactness 136Ч137
Cohomology and non-orientability 136Ч137
Cohomology groups 120
Cohomology groups for  136 136
Cohomology groups for 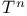 136 136
Cohomology groups, calculation of 127Ч136
Cohomology groups, de Rham 123Ч139
Cohomology groupsfor a general manifold 136
Cohomology versus homology 138Ч139
Cohomology with real coefficients 121
Compact set 16Ч19
Compactness 16Ч19 22Ч23
Compactness, topological invariance of 22Ч23
Complex orthogonal group 285Ч288
Complex projective space 138 217 287Ч288
Complex projective space and  -planes 287Ч288 -planes 287Ч288
Complex projective space and spin structures 217
Complex structures 170Ч171 291
Conformal invariance 259Ч260
Conformal invariance of the * operation 260
Conformal invariance of the action S 260
Connected set 19Ч20
Connectedness 19Ч20 22Ч23 53
Connectedness, path 53
Connectedness, topological invariance of 22Ч23
Connection form 177Ч178
Connections 174Ч198 256Ч303
Connections in the tangent bundle 184Ч194
Connections, Levi Ч Civita 191Ч194
Connections, Maxwell 196Ч198 297Ч298
Connections, physical significance of 301Ч302
Connections, Yang Ч Mills 194Ч196 256Ч303
Continuity 9Ч12
Continuous deformation 9 25
Contractibility of Gl(n,C) to U(n) 163Ч164
Contractibility of Gl(n,R) to O(n) 162
Contractibility to a maximal compact subgroup 163
Contractible manifold 125Ч127
Contractible manifold, definition of 125
Contravariant vector 39Ч40
Cotangent bundle 150 166
Covariant derivative 174 179Ч180 183Ч187
Covariant exterior derivative 181Ч182
Covariant vector 39Ч40 42
Covering space 254
Critical point 227
Cup product 137Ч138
Cup product and ring structure of H*(M;R) 138
Curvature 179Ч181
Curvature and lack of commutativity of covariant differentiation 179Ч180
Curvature tensor 180Ч181 188
Curvature, dual of 183
CYCLE 86
defects 244Ч255
Defects, combination rule for line defects 249
Defects, crossing of line defects 251Ч253
Defects, definition of 246
Defects, stability of 246
Deformation 1
Deformation retract 64 135
Dense set 16
Diffeomorphism 49 221
Differentiable structures 49Ч50
Differentiable structures, different 49
Differential 40
Differential form see "r-form"
Differential geometry 25Ч50 171Ч225
DIMENSION 23Ч24
Dimension, topological invariance of for  23Ч24 23Ч24
Dimension, topological invariance of for a manifold 26
disconnected set 20
Dual 39Ч40
Dual basis 40
Dual of a linear map 39Ч40
Dual of a vector space 39
Dynamical system 8
Equivalence of T(M) and T*(M) 163
Euler class 204 210Ч211 215Ч217 220
Euler class and Pfaffian 211
Euler Lagrange equations 257
Euler Ч Poincare characteristic 140
Euler Ч Poincare formula 106
Exact form 123
Exact sequences 99 123
Exact sequences of a fibre bundle 253
Exact sequences of homology groups 99
Exact sequences of homotopy groups 115Ч116
Exact sequences, application of exact homology sequence 100Ч104
Exact sequences, theorem for four groups 100
Excision theorem 98
Exterior algebra 42
Exterior derivative 41Ч43 121Ч123
Fibre bundle 140Ч225
Fibre bundle, base space of 142
Fibre bundle, classification of 200Ч212
Fibre bundle, contraction of the base space of 159Ч165
Fibre bundle, definition of 142
Fibre bundle, fibre of 142
Fibre bundle, list of 151
Fibre bundle, local triviality of 142
Fibre bundle, principal 152Ч156 261
Fibre bundle, projection of 142
Fibre bundle, reconstruction from transition functions 144Ч147
Fibre bundle, reduction of the group of 159Ч165
Fibre bundle, section of 152Ч156
| Fibre bundle, structure group of 142
Fibre bundle, total space of 142
Fibre bundle, transition functions of 142
Fibre bundle, triviality of 152Ч156
Fibre bundle, triviality of over a contractible base 161
Finitely generated group 90
Fixed points 4Ч8
Fixed points of an operator 6Ч8
Fixed points of the disc 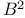 4Ч7 4Ч7
Flow of a vector field 169
Freely generated group 90
Functions 9Ч12
Functions with discontinuity 10Ч11
Functions, continuous 9
Fundamental group 51Ч78
Fundamental group of 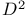 71 71
Fundamental group of 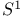 71 71
Fundamental group of  72 72
Fundamental group of a product 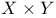 77 77
Fundamental group of Klein bottle 76
Fundamental group of Moebius band 72
Fundamental group of projective plane 75
Fundamental group of torus 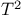 74 74
Fundamental group, definition of 56
Fundamental group, dependence on base point 58
Fundamental group, non-abelian nature of 66
Fundamental group, the calculating theorem 68
Fundamental theorem of algebra 3
G-structures 163Ч171
G-structures, topological restrictions to existence of 164 167Ч171
Gauge potential 178 299 see
Gauge potential, static 299
Gauss Ч Bonnet theorem 140 223Ч225
Generators of an Abelian group 90
Geodesics 190Ч191
GL(n,R) 149Ч152
Global invariants and local geometry 221Ч225
Grassmann manifold 201 205Ч206
Grassmann manifold, complex 205
Grassmann manifold, oriented 205
Hamiltonian manifold 166
Hamiltonian structures 166Ч171
Hamiltonian structures and classical phase space 166
Hamiltonian structures and Hamilton's equations 168Ч169
Hausdorff space 27Ч28
hessian 227
Holes in a manifold and cohomology 131
Holomorphic structure 292Ч297
Holomorphic vector bundle 291Ч297
Homeomorphism 20Ч24 26 221Ч222
Homeomorphism and continuous deformation 20
Homeomorphism and equivalence classes 20Ч22
Homeomorphism as a continuous invertible map 23
Homology groups 79Ч108 120
Homology groups of 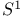 89 89
Homology groups of  104 104
Homology groups of a connected polyhedron 89
Homology groups of a contractible space 87
Homology groups of D2 87
Homology groups of projective plane 91
Homology groups, definition of 86
Homology groups, excision theorem of 98
Homology groups, simplicial 79
Homology groups, singular 107
Homology groups, torsion subgroup of 91
Homotopy 21Ч22 128Ч129 135 160Ч161 244Ч255 260Ч262
Homotopy and defects 244Ч255
Homotopy and instantons 260Ч262
Homotopy and pullback bundles 160Ч161
Homotopy group 109Ч119
Homotopy group Abelian nature for n>1 112
Homotopy group of  118 118
Homotopy group, definition for n>1 111
Homotopy group, first see "Fundamental group"
Homotopy of maps 21Ч22 128Ч129 135
Homotopy type 60
Homotopy, invariants 22
Hopf map 225
Horizontal lift 175 184 187 195
Horizontal subspace 175Ч177
Hurewicz Theorem 118
Induced bundle see "Pullback bundle"
instantons 256Ч297
Instantons and absolute minima 263Ч265
Instantons and finite action 259Ч260
Instantons and holomorphic vector bundles 289Ч294
Instantons and Minkowski space 297
Instantons and the second Chern class 269Ч272
Instantons and twistor methods 283Ч288
Instantons with k=1 265Ч269
Instantons with k>1 272 278Ч282
Instantons, construction of from holomorphic vector bundles 295Ч296
Instantons, topology and boundary conditions 260Ч262
Integral curves 172
Integration of 44Ч48
Integration of r-forms 44Ч49
Invariant polynomials 207Ч210
Invariant polynomials, homogeneity of 207
Invariants 221Ч225
Invariants of complex structure 221Ч222
Invariants of differential structure 221Ч222
Invariants of topological structure 221Ч225
Isotopy 21
Jacobi identity 182
Jacobian determinant 34Ч35 46
Jacobian matrix 150Ч151
k-cell 231
K-theory 139
Killing form 256
Kunneth formula 105
Lagrangian 256
Landau theory 236
Lie derivative 171Ч174
Linear independence and vector fields 157Ч158
Liouvilles theorem 296
Local product 141Ч143
Loop 53
Loop, homotopy of 54
Loop, inverse of 54
Loop, product of 54
Lorentz structures 171
Manifold 25Ч50 137
Manifold, definition of 26
Manifold, infinite dimensional 49
Manifold, orientable 137
Manifold, pseudo-Riemannian 29
Manifold, Riemannian 29 46
Maxwell's equations 197 298
Metric 164
Metric space 28Ч29
Metric, signature of 164
Minkowski space 258 297
Minkowski space, compactified 297
Moebius strip 34Ч35 137 141Ч148 152Ч156
Moebius strip as a fibre bundle 141Ч148
Moebius strip, principal bundle associated with 152Ч156
Monopoles 297Ч303
Monopoles and holomorphic vector bundles 301
Monopoles, Abelian 297Ч298
Monopoles, topological charge of 299Ч300
Morse inequalities 229
Morse inequalities, proof of 233Ч236
Morse lemma 229
Morse theory 49 227Ч243
Multi-instantons 272 278Ч282
N-loop 109
n-loop, homotopy of 110
n-loop, product of 110
Neighbourhoods 13
Nematic liquid crystal 250
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -planes
-planes  -planes
-planes