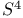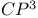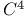|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Nash C., Sen S. — Topology and geometry for physicists |
|
|
 |
| Предметный указатель |
Non-compact set 16—17
One-form 40
Open covering 16—18 45
Open covering, bounded 17
Open covering, intersection of 9
Open sets 9 17
Open sets, union of 9
Ordered medium 246
Orientability 33—37 260
Orientability, and the * operation 260
Orientability, definition of 36—37
p-chains 120—122
p-forms 122
Paracompactness 46
Parallel transport 174—175 178—179 187
Parallelizability 157—158
Parallelizability of  158 158
Parallelizable manifolds 157—198
Parallelizable manifolds and Lie groups 157
Partition of unity 45—46 132—133
Path 51
Path, definition of 51
Path, product of 59
Permutation symbol 182
Pfaffian see "Euler class"
Poincare's lemma 123—127
Polyhedron 68
Pontrjagin classes 204—206 210—211 215—217
Positive real form 294
Presentation of a group 69
Principal fibre bundle see "Fibre bundle"
Projective twister space see "Twister space"
Pseudo-Riemannian geometry 164
Pullback bundle 159—161 202—206
Pullback forms 44 183
Punctured plane 124
Quaternionic linear algebra 297
Quaternionic matrix 282
Quaternionic projective space 284
Quaternions 272—282
Quaternions and instantons with k>1 278—282
Quaternions and SU(2)-connections 272—276
Quaternions and the k=1 instanton 276—278
r-form 42—48
Rank 90 149
Rank of a complex vector bundle 149
Rank of a real vector bundle 149
Rank of an abelian group 90
Real projective space 137
Relative boundary 95
Relative chain 95
Relative cycle 96
Relative homology group 95—104
Relative homology group of 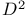 96 96
Relative homology group, definition of 96
Relative homotopy groups 113—118
Relative homotopy groups, definition of 115
Relative n-loop 114
Relative n-loop, definition of 114
Relative n-loop, product of 114
retract 63
Riemannian metric 162—163
Riemannian metric, existence of 162
Section see "Under Fibre bundle"
Self-duality 259 263—283 286 299
Self-duality and  -planes 286 -planes 286
Self-duality and the Bogomolny equation 299
Self-duality, definition of 259
Sets see "Names of specific kinds of set"
Sets, boundary of 15
Sets, closure of 14 16
Sets, cover of 16—18
Sets, interior of 15
Sheaf cohomology 294
simplex 67
Simplex, barycentric coordinates of 67
Simplex, definition of 67
Simplex, dimension of 68
Simplex, face of 67
Simplex, oriented 83
Simplicial complex 68
Simplicial complex, definition of 68
Simplicial complex, path connectedness of 68
Smooth manifold 26
Spin structures see "Stiefel — Whitney classes"
Stereographic projection 133—135 259—260
Stereographic projection and instantons 259—260
| Stiefel manifold 201
Stiefel — Whitney classes 205—206 212 221—222
Stiefel — Whitney classes and orientability 212
Stiefel — Whitney classes and spin structures 212
Stokes' theorem 47—48 120 122
Stokes' theorem and fundamental theorem of calculus 48
Structure group 142 149—152
Structure group for cotangent bundle 151
Structure group for tangent bundle 149
Structure group for tensor bundle 151
Sub-additive function 232
Subcovering 16—19
surface 33—35
Surface, non-orientable 34
Surface, one-sided 33—34
Surface, orientable 33
Surface, two-sided 33
Symmetry breaking selection rules 236—242
Symplectic manifold 166
Symplectic structure see "Hamiltonian structure"
Tangent bundle 140 148—150
Tangent bundle, local product structure of 149
Tangent bundle, structure group of 149
Tangent space 39 43—44
Tangent vector 37—39 149—150
Tensor bundle 151
Tensor field 41
Tensors 41—43
Tensors, antisymmetric covariant 42
Tensors, covariant 42
Tensors, definion of 41
textures 244 253
Topological invariants 21—24
Topological invariants and homotopy 22
Topological reasoning 1—8
Topological space 8—24 26
Topological space, definition of 8—12
topology 9 12—16 24
Topology, coarser 12—13
Topology, discrete 9 12
Topology, finer 12—13
Topology, indiscrete 9 12
Topology, largest 12—13
Topology, relative 24
Topology, smallest 12—13
Topology, stronger 13
Topology, trivial 9
Topology, usual 9 13—14 16
Topology, weaker 13
Torsion 91 105
Torsion tensor 187—194
Torsion tensor, geometrical interpretation of 192—194
Torus 30—33
Torus flat 32—33
Torus, n-dimensional 31
Torus, two—dimensional 31—33
Transition functions 142—148 150—152 154 262
Transition functions and gauge transforma tions 148
Transition functions and SU(2)-bundles over 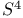 262 262
Transition functions for cotangent bundle 150
Transition functions for Mobius strip 143 145—147 151
Transition functions for tangent bundle 150
Transition functions for tensor bundle 151
Transition functions non-uniqueness of 147—148
Transition functions, factorisation of and triviality 154
Transition matrix see "Transition function"
Triangulation of a space 70
Twistor space 283—289
Twistor space and 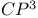 283—285 283—285
Twistor space and 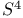 284—285 284—285
Twistor space and planes in 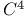 285—288 285—288
Type, of a complex differential form 290
Unitary structure 292—293
Universal bundles 201—206 211—212
Vector bundle 140 149—150 211—212
Vector field 5—8 41 156—158
Vector field, index of 5—6
Vector field, singularities of 8 156—158
Vector field, zero of 5—8
Velocity vector 38
Vertical subspace 175—177 291
Volume element 44—46
Wedge product 41—42
Whitney sum 198
Yang — Mills field 183 256—303
Yang — Mills field, equation of motion of 183
Yang — Mills field, quantization of 302—303
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




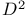
 -planes
-planes