Авторизация
Поиск по указателям
Cox D., Little J., O'Shea D. — Ideals, varieties, and algorithms
Обсудите книгу на научном форуме Нашли опечатку?
Название: Ideals, varieties, and algorithmsАвторы: Cox D., Little J., O'Shea D.Аннотация: Algebraic Geometry is the study of systems of polynomial equations in one or more variables, asking such questions as: Does the system have finitely many solutions, and if so how can one find them? And if there are infinitely many solutions, how can they be described and manipulated? The solutions of a system of polynomial equations form a geometric object called a variety; the corresponding algebraic object is an ideal. There is a close relationship between ideals and varieties which reveals the intimate link between algebra and geometry. Written at a level appropriate to undergraduates, this book covers such topics as the Hilbert Basis Theorem, the Nullstellensatz, invariant theory, projective geometry, and dimension theory.
The algorithms to answer questions such as those posed above are an important part of algebraic geometry. This book bases its discussion of algorithms on a generalization of the division algorithm for polynomials in one variable that was only discovered it the 1960's. Although the algorithmic roots of algebraic geometry are old, the computational aspects were neglected earlier in this century. This has changed in recent years, and new algorithms, coupled with the power of fast computers, have let to some interesting applications, for example in robotics and in geometric Theorem proving.
In preparing a new edition of "Ideals, Varieties and Algorithms" the authors present an improved proof of the Buchberger Criterion as well as a proof of Bezout's Theorem. Appendix C contains a new section on Axiom and an update about Maple, Mathematica and REDUCE.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2-nd editionГод издания: 2006Количество страниц: 553Добавлена в каталог: 08.12.2013Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
15 330 2 Adams, W. 206 517 522 Admissible geometric theorem 289ff Affine, cone over a projective variety see "Cone affine" Affine, Dimension Theorem see "Theorem Dimension" Agnesi, M. 24 Algebraic relation 338 Algebraically independent 294 466 469 470 Algorithm 37 142 Algorithm, algebra (subring) membership 334 Algorithm, associated primes 209 Algorithm, Buchberger’s 87 92 99 100 106 108 377 519 521 Algorithm, computation in 230 Algorithm, consistency 170 Algorithm, dimension (affine variety) 451 468 Algorithm, dimension (projective variety) 453 Algorithm, division 37ff 157 220 Algorithm, division in 33 59ff 93 194 226 227 377 518 Algorithm, division in k[x] 302 303 Algorithm, Euclidean 41 92 149 152 156 157 178 179 Algorithm, finiteness of solutions 230 Algorithm, Gaussian elimination (row reduction) 9 49 50 52 91 154 304 Algorithm, greatest common divisor 187 Algorithm, ideal equality 91 Algorithm, ideal intersection 186 194 202 Algorithm, ideal membership 34 43 93 Algorithm, ideal quotient 194 202 Algorithm, irreducibility 205 Algorithm, least common multiple 187 Algorithm, polynomial implicitization 127 Algorithm, primality 205 Algorithm, primary decomposition 209 Algorithm, projective closure 382 Algorithm, projective elimination 393 Algorithm, pseudodivision 303 Algorithm, radical 233 Algorithm, radical membership 176 292 Algorithm, rational implicitization 130 Algorithm, Ritt’s decomposition 304 309 520 Algorithm, tangent cone 485ff Algorithm, Wu — Ritt 309 510 Altitude 299 Anderson, D. 131 521 artificial intelligence 286 Ascending chain condition (acc) 76 77 201 373 391 Associated primes question 209 Atiyah, M. 209 Automated geometric theorem proving 286ff Automorphism of varieties 242 Axiom see "Computer algebra systems" Baillieul, J. 282 Bajaj, C. 154 521 Barrow, I. 24 Basis, minimal 35 71 72 Basis, of an ideal see "Ideal basis Basis, standard 74 76 Bayer, D. 72 109 119 519 Becker, J. 517 Becker, T. 80 108 176 186 206 233 278 522 Benson, C.T. 323 334 335 520 Bernoulli, J. 24 Bezier, P. 20 Billera, L. 520 Birationally equivalent varieties 250ff 470 Blow-up 494 495 Boege, W. 513 521 Brieskom, E. 424 428 520 Bruce, J.W. 134 139 143 Buchberger, B. 75 84 88 108 227 282 Canny, J. 131 154 Centroid 299 Chain, ascending, of ideals 76 78 Chain, descending, of varieties 79 201 373 Char, B. 509 Characteristic of a field see "Field" Characteristic sets 304 309 520 Chou, S.C. 309 520 Circumcenter 299 Cissoid of Diodes see "Curve cissoid Classification of varieties 217 252 Clemens, H. 424 Closure, projective 381 394 401 454 461 Closure, Zariski 122 190 191 197 254 CoCoa see "Computer algebra systems" Coefficient 2 Collinear 288 299 Comaximal ideals 189 Complement of a monomial ideal 433ff Complete intersection 464 complexity 108 109 519 Computer algebra systems 37 39 42 56 65 66 90 98 100 133 149 164 203 206 209 234 285 293 303 455 505ff 518ff Computer algebra systems, AXIOM 37 176 206 209 505ff Computer algebra systems, CoCoA 455 516ff Computer algebra systems, Macaulay 176 206 455 516ff Computer algebra systems, MACSYMA 516 Computer algebra systems, Magma 517 Computer algebra systems, Maple 37 508ff Computer algebra systems, MAS 517 Computer algebra systems, Mathematica 37 510ff Computer algebra systems, PoSSo 517 Computer algebra systems, REDUCE 37 176 206 209 455 512ff 521 Computer algebra systems, SCRATCHPAD 505 Computer algebra systems, SINGULAR 517 Computer graphics 521 Computer-aided geometric design (CAGD) 20 22 Cone, affine 368 369 374 453 485 Cone, projectivized tangent 495 Cone, tangent 485ff Configuration space see "Space configuration Congruence (mod I) 219 Conic section 27 133 351 358 399 401 415 426 Consistency question 11 45 170 Constructible set 123 259 260 Control points 21 Control polygon 21 Coordinate 235 Coordinate ring of a variety (k[V]) see "Ring coordinate Coordinate subspace 430 435 467 Coordinate subspace, translate of 436 437 439 Coordinate, Pluecker 408ff coordinates 235 Coordinates, homogeneous 352 360 Coordinates, Pluecker 412 Coset 347 Cox, D. 118 233 521 522 Coxeter, H.S.M. 323 Cramer’s Rule 390 500 Cross ratio 298 cube 322 327 328 Cubic, Bezier 20ff 27 520 Cubic, twisted see "Curve twisted Curve, cissoid of Diodes 25 26 Curve, dual 348 Curve, family of 138 Curve, folium of Descartes 133 Curve, four-leaved rose 12 13 144 Curve, rational normal 383 384 Curve, twisted cubic 7 8 19 32 66 84 97 125 127 131 172 195 212 217 244 245 364 366 368 370 379—382 450 464—466 Cuspidal edge 245 Czapor, S. 521 Davenport, J.H. 39 42 44 149 188 Decomposition, minimal, of a variety 203 373 476 Decomposition, minimal, of an ideal 204 Decomposition, primary 206ff Decomposition, question 206 Degenerate case of a geometric configuration 294 307 Degeneration 428 Degree of a projective variety 465 Degree, total, of a monomial 2 438 Degree, total, of a polynomial 2 Degree, transcendence, of a field extension 470 Dehomogenization of a polynomial 363 486 Dehomogenization of an ideal 392 Derivative, formal 46 226 474 Descending chain condition (DCC) 79 201 259 373 Desingularization 495 Determinant 151 417 499 Determinant, Vandermonde 44 Dickson’s Lemma 69 Difference of varieties 14 191 DIMENSION 8ff 11 233 279 430 431 436 439 442 450 453 457ff 466 468—471 480 481 Dimension at a point 478 491 Dimension, question 11 426ff Discriminant 155 319 dodecahedron 328 Dominating map 472 Dual curve 348 Dual projective plane 359 399 Dual projective space 369 407 Dual variety 348 Duality of polyhedra 328 Duality, projective principle of 351 Dube, T. 108 Echelon matrix 49 75 92 410 412 Eisenbud, D. 176 206 517 522 Elimination order see "Monomial ordering elimination" Elimination step 113 Elimination theory 17 112ff Elimination theory, projective 384ff Envelope 139ff Equivalence, birational 250 470 473 Equivalence, projective 399 404 Euler line 299 Euler’s formula 369 Extension step 113 Factorization of polynomials 146ff 164 Family of curves see "Curve family Farin, G. 520 Faugere, J. 519 Feiner, S. 521 Fiber 259 Field 1 497 520 Field of characteristic zero 180 482 Field of finite (positive) characteristic 180 402 404 410 482 Field of fractions of a domain 254 Field of rational functions (k(V)) 147 246 463 469 473 Field, algebraically closed 4 34 124 163 168 170 172 174 175 192 196 199 200 204 210 230 231 254 374—376 382 389 394 395 404 405 417 451 453 458—462 469 486 Field, finite 3—5 36 Field, fractions of a domain 245 Field, infinite 3 4 32 126 130 172 196 342 372 Final remainder (in Wu’s method) 306 Finite Generation of Invariants 327 333 336 Finiteness question 11 230 235 460 Finkbeiner, D.T. 156 166 404 469 499 500 Foley, J. 521 Folium of Descartes see "Curve folium Follows generically from 295 Follows strictly from 292 Forward kinematic problem see "Kinematics problem of robotics forward" Fulton, W. 423 424 Function field see "Field of Function, algebraic 119 Function, coordinate 235 Function, polynomial 3 213 Function, rational 15 119 245 473 Garrity, T. 154 520 521 Gauss, C.F 314 Gaussian elimination see "Algorithm Gaussian Gebauer, R. 108 513 521 Gelfand, I. 154 Gianni, P. 176 206 519 Giblin, P.J. 134 139 143 Giovini, A. 108 521 Giusti, M. 109 GL(n,k) see "Group general Goldman, R. 131 521 Goldstine, S. 511 Grabe, H.G. 516 Graded lexicographic order see "Monomial ordering" Graded monomial order see "Monomial ordering" Graded reverse lexicographic order see "Monomial ordering" Gradient 10 136 137 Graph 6 126 Grassmannian 409 greatest common divisor (GCD) 40ff 178 187 Greuel, G.-M. 517 Griffiths, P. 424 Gritzmann, P. 109 Groebner basis 31 44 74ff 113ff 127 128 130 160 170 176 186 194 226ff 244 275ff 284 293 302 309 314 316 334ff 340ff 382 388 394 485ff 519ff Groebner basis, comprehensive 278 522 Groebner basis, conversion 519 Groebner basis, criterion for 82 104 Groebner basis, minimal 89 92 Groebner basis, reduced 90 92 170 176 292 296 374 Groebner basis, specialization of 276 278 283ff Groebner basis, universal 522 Groebner, W. 75 Group 498 Group of symmetries of a cube 322 327 347 Group of symmetries of a tetrahedron 328 Group, cyclic 322 Group, finite matrix 321ff Group, general linear (GL(n,k)) 321 410 418 498 Group, generators for 325 Group, Klein four- 326 Group, orbit of a point under 343 Group, permutation 322 499 Group, projective general linear (PGL(n,k)) 410 Group, subgroup of 499 Grove, L.C. 323 334 335 520 Heintz, J. 109 Hermann, G. 176 206 Herstein, I.N. 318 521 Hilbert function 452 452 459 Hilbert function, affine 447 467 Hilbert, D. 74 168 311 335 433 Hironaka, H. 76 Hodge, W.V.D. 410 Hoffmann, C. 519 520 Homogenization of a polynomial 172 364 Homogenization of an ideal 378 453 486 Hughes, J. 521 Huneke, C. 176 206 Hyperboloid 247 Hyperplane 363 400 Hyperplane at infinity 361 461 Hypersurface 363 458 461 Hypersurface, cubic 363 Hypersurface, nonsingular quadric 405 Hypersurface, quadric 363 401ff 404 Hypersurface, quartic 363 Hypersurface, quintic 363 icosahedron 328 Ideal 29 498 Ideal description question 34 47 73 Ideal membership question 34 44 47 65 70 80 93 519 Ideal of a variety (I(V)) 31 372 Ideal of leading terms 73 Ideal of relations 339 Ideal, basis of 30 35 Ideal, colon 191 Ideal, complete intersection 464 Ideal, determinantal 110 Ideal, elimination 113 340 394 Ideal, generated by a set of polynomials 29 Ideal, Groebner basis of see "Groebner basis" Ideal, homogeneous 363 371 377 Ideal, in a ring 223
Реклама
 |
|
О проекте
|
|
О проекте



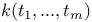
![$k[f_{1},...,f_{m}]$](/math_tex/5280d32a23bc3cce22537ca99f6106c182.gif)
![$k[x_{1},...,x_{n}]$](/math_tex/a9490b5ea4f6ca1ea780cfc0f1af792082.gif)
![$k[x_{1},...,x_{n}]/I$](/math_tex/292b15b45acc60a668735a47493e591382.gif)