|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cvitanovic P. — Group theory (Lie and other) |
|
|
 |
| Предметный указатель |
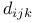 tensor 102 214 tensor 102 214
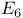 193—212 193—212
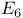 , Springer construction 211—212 , Springer construction 211—212
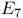 221—232 221—232
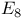 181—191 181—191
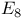 family, primitiveness assumption 181 family, primitiveness assumption 181
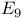 triality 207 triality 207
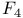 213—220 213—220
 169—180 169—180
 , evaluation rules 253—258 , evaluation rules 253—258
3-j coefficient 43
3-j SU(n) 95
3-j symbol 43
3-j symbol, SU(n) 94—97
3-vertex, spinster 155
3n-j coefficient 39 43
6-j coefficient 43
6-j coefficient, spinorial 138—140
6-j symbols 43
Abelian group 16
Adjoint rep, reality 35
Adjoint rep, SU(n) 107
Adjoint, rep, dimension 32
Adjoint, space 32 33
Adjoint, tensor, 2-index SU(n) 101
Adjoint, tensor, SU(n) 99
Algebra 17
Algebra, associative 17
Algebra, Lie 17
Algebra, of invariants 22
Antisymmetric tensors 58
Antisymmetrization operator 52
Associative algebra 17
Betti number 63
Binor 158 159
Birdtracks 27—37 39
Bra-ket formalism 46
Cartan canonical basis 35 38
Cartan roots 42
Cartan spinor 129
Cartan, E. 129
Cartan-Killing form 35
Casimir 59—75
Casimir orthogonality 68
Casimir quartic 70—75
Casimir SU(n) 105
Casimir symmetrized 61
CHARACTER 82—83
Character, orthonormality 82
Character, SU(n) 97
Characteristic equation 57
Characteristic equation, 3-index tensor, SU(n) 86
Characteristic equation, unitary 2-index tensor 85
Clebsch 29 29—32
Clebsch — Gordan series 43 81
Clebsch, irrelevancy 38
Clifford algebra, Grassmann extension 153 157
Color algorithm, dimension 93
Commutator, Lie algebra 37 38
Commutator, Lorentz group 38
Completeness relation 31
Completeness, relation 25 42
Completeness, spinster 155
Completeness, Wigner 3-j 158
Complex vector space 16
Conjugate, hermitian 19
Conjugate, rep 18
Conjugate, vector space 17
Coordinate reflection 32
Cubic invariant SU(3) 163—165
Curvature scalar 126
Cyclic group 16
Decomposition 93
Decomposition, irreducible 26
Defining, rep 18
Defining, rep, irreducible 26
Defining, vector space 17
Deligne, R. 191
Diagonalizing matrix 24
Dimension, adjoint rep 32
Dimension, color algorithm 93
Dimension, group 32
Dimension, Lie algebra 32
Dimension, SO(n) 127
Dimension, SU(n) 89
Dimension, U(n) 92
Dirac  matrix 42 129—144 167 173 matrix 42 129—144 167 173
Dirac  matrix, Grassmann 153 matrix, Grassmann 153
Dirac, P. 129 153
Direct product, Young tableau 90
Dual vector space 17
Dynkin diagram 75
Dynkin index 64—69
Dynkin index, cubic 69
Dynkin index, quadratic 65 69
Dynkin index, SU(n) 2-index tensor 86
Dynkin index, sum rules 68
Dynkin label 75
Dynkin label, SU(n) 89
Dynkin labels, SO(n) 127
Elvang, E. 242
Feynman diagram 27 39
Fierz coefficients 133—138
Fierz identity 136
Gell — Mann, 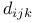 tensor 102 214 tensor 102 214
Gell — Mann,  matrix 33 38 42 matrix 33 38 42
Generator transformation 32
Grand unified theories 70
Grassmann 153
Grassmann, Clifford algebra 153
Grassmann, extension, Clifford algebra 157
Gravity tensors 124
Group 15—16
Group, 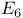 193—212 193—212
Group, 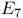 221—232 221—232
Group, 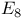 181—191 181—191
Group, 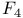 213—220 213—220
Group,  169—180 169—180
Group,  , evaluation rules 253—258 , evaluation rules 253—258
Group, abelian 16
Group, cyclic 16
Group, dimension 32
Group, integral 79—84
Group, integral, SU(n) 83
Group, invariance 23
Group, isomorphic 16
Group, order 15
Group, SO(n) 115—128
Group, SO(n), spinor reps 129—144
Group, Sp(n) 145
Group, spinster reps 153—159
Group, SU(3) 163—165
Group, SU(n) 161—168
Group, U(n) 85—107
Group, U(n), Young proj. oper 247—251
Group, unitary 18
Handedness, spinorial 142—143
Heisenberg algebra 153 159
Hermitian conjugation 19 28
Hermitian matrix 19
IHX relation 40
Index summation, repeated 18
Infinitesimal transformation 32—38
Inner product, space 16
Invariance, condition 34
Invariance, group 23
Invariant 20
Invariant, algebra 22
Invariant, composed 20
Invariant, matrix 20
| Invariant, tensor 19
Invariant, tensor, operator 47
Invariant, tensor, primitive 21
Invariant, tree 21
Invariant, vector 19
Irreducible, decomposition 26
Irreducible, rep 26 81
Isomorphic group 16
Jacobi relation 37 171 181
Johansen, A. 242
k-standard arrangement 8 ?
Kahane algorithm 143—144
Klein — Nishina cross-section 129
Kronecker delta 23
Lattice gauge theories 70
Levi — Civita tensor 21 166
Levinson 46
Lie algebra 17 35—38
Lie algebra, commutator 37 38
Lie algebra, dimension 32
Lie algebra, SO(n) 38
Lie algebra, U(n) 38
Lie product 17
Linear space 16
Lorentz group, commutator 38
Magic Triangle 235—236
Matrix, diagonalizing 24
Matrix, hermitian 19
Matrix, invariant 20
Matrix, product 17
Matrix, rep 17
Metaplectic reps, Sp(n) 153
Multi-particle state 88
Multiplication, scalar 16
Negative dimensions 146 149—152 221
Negative dimensions, spinsters 157
Negative dimensions, SU(n) 3-j 95
Normalization, Young proj. operator 248
Observables, simultaneous 25
Okubo, S. 190
Order of a group 15
Orthogonality, casimir 68
Orthogonality, relation 25 31
Orthogonality, spinor 133
Orthogonality, spinster 155
Orthogonality, Wigner 3-j 158
Orthogonality, Young projection operators 249
Orthosymplectic group 159
Pauli matrix 33
Penrose, R. 158 159
permutations 49—58
Phase convention 43
Primitive invariant tensor 21
Primitiveness assumption 21
Primitiveness assumption, 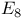 family 181 family 181
Product, Lie 17
Product, matrix 17
Product, scalar 16
Projection operator 24—26 29—32
Propagator 27 39
Quartic casimir 70—75
Quartic casimir relations 72
Racah coefficient 158
Recoupling coefficient, spinster 156
Recoupling relation 43
Reduced matrix elements 45—47
Reflection, coordinate 32
Rep, character 82
Rep, conjugate 18
Rep, defining 18
Rep, dimension spinster 157
Rep, irreducible 26 81
Rep, matrix 17
Rep, SU(n) 88
Rep, tensor 18
Repeated index summation 18
Ricci tensor 126
Riemann — Christoffel tensor 124
Scalar multiplication 16
Scalar product 16
Schur's lemma 46
Sextonians 178
Simultaneous observables 25
Singlet 80
SO(N) 115—128
SO(n) casimirs 62
SO(n) dimensions 127
SO(n) Dynkin labels 127
SO(n) Lie algebra 38
SO(n) spinor reps 129—144
Sp(N) 145
Sp(n) casimirs 62
Sp(n) metaplectic reps 153
Sp(n) spinster reps 153—159
Space, adjoint 33
Space, complex vector 16
Space, conjugate vector 17
Space, defining vector 17
Space, dual vector 17
Space, inner product 16
Space, linear 16
Space, vector 16
Spinography 130—144
Spinor 129—144
Spinor, dimension sum rule 135
Spinor, handedness 142—143
Spinor, Kahane algorithm 143—144
Spinor, orthogonality 133
Spinster 153—159
Spinster, completeness 155
Spinster, orthogonality 155
Spinster, recoupling coefficient 156
Spinster, rep dimension 157
Spinster, trace 155
Springer construction of 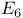 211—212 211—212
Structure constant 17 36
STU relation 40
SU(2), Young tableau 89
SU(3) 163—165
SU(N) 161—168
SU(n) 3-j 94
SU(n) adjoint rep 107
SU(n) adjoint tensor 99
SU(n) basis vectors 94
SU(n) casimirs 105
SU(n) characters 97
SU(n) decomposition 93
SU(n) dimension 89
SU(n) Dynkin label 89
SU(n) Lie algebra 38
SU(n) Young tableaux 88
Subgroup 16
Subgroup, embedding 38
Sum rule, spinor dimensions 135
Sum rule, SU(n) 3-j 96
Symmetric tensors 57
Symmetrization operator 50
Symmetry, breaking 38
Tensor 18
Tensor, 2-index SU(n) 85
Tensor, 3-index SO(n) 121
Tensor, decomposition 93
Tensor, fully antisymmetric 58
Tensor, fully symmetric 57
Tensor, gravity 124
Tensor, invariant 19
Tensor, mixed adjoint  defining SO(n) 117 defining SO(n) 117
Tensor, mixed adjoint 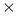 defining SU(n) 97 defining SU(n) 97
Tensor, operator, invariant 47
Tensor, rep 18
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



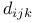 tensor
tensor 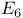
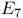
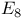
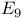 triality
triality 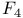

 matrix
matrix  matrix
matrix  defining SO(n)
defining SO(n)  defining SU(n)
defining SU(n)