|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cvitanovic P. — Group theory (Lie and other) |
|
|
 |
| Предметный указатель |
Tensor, SU(n) 86
Three-index tensor, SO(n) 121
Three-index tensor, SU(n) 86
Trace, spinster 155
Transformation, generator 32
Transformation, infinitesimal 32—38
Tree, invariant 21
Triality, 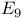 207 207
Trivalent graphs 40
Two-index tensor, adjoint SO(n) 118
Two-index tensor, SO(n) 116
Two-index tensor, SU(n) 85
Two-index tensor, SU(n) adjoint 101
Two-index tensor, Young tableau 89
U(n) 85—107
U(n) rep dimension 92 93
U(n) Young proj. oper 247—251
U(n), Lie algebra 38
Unitary group 18
Vacuum bubbles 44 46
Vanagas 46
Vanishing tensors 75
Vector invariant 19
Vector space 16
Vector space, complex 16
Vector space, conjugate 17
Vector space, defining 17
Vector space, dual 17
Vogel, P. 191
Weak coupling expansions 70
Weyl tensor 126
Weyl, H. 129 135
| Wigner 3-j completeness 158
Wigner 3-j orthogonality 158
Wigner 3n-j coefficient 39
Wigner 3n-j symbols 43
Wigner 6j coefficient 63
Wigner — Eckart theorem 45
Young diagram 87
Young diagram, definition 87
Young diagram, k-standard arrangement 88
Young diagram, length 91
Young polynomial 92
Young projection operator 90—92
Young projection operator, 3-j 94
Young projection operator, basis vectors 94
Young projection operator, completeness 94
Young projection operator, decomposition 93
Young projection operator, normalization 91 248
Young projection operator, orthogonality 249
Young projection operator, properties 91 247—251
Young tableau 87—90
Young tableau, 2-index tensor 89
Young tableau, 3-j 94
Young tableau, conjugate 89
Young tableau, decomposition 93
Young tableau, definition 88
Young tableau, Kronecker product reduction 90
Young tableau, standard arrangement 88
Young tableau, SU(2) 89
Young tableau, SU(n) 88
Young tableau, transpose 88
Young tableau, U(n) dimension 92
Yutsis 46
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте