|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Fenstad J.E. — General recursion theory: An axiomatic approach |
|
|
 |
| Предметный указатель |
Aanderaa, S. [1] 83 85
Abstract 1-section 135
Acceptable structure 87
Aczel, P. [2] 42
Aczel, P. [3] 67 82 83
Aczel, P. [4] 79 82
Aczel, P. [5] 124
Aczel, P. [6] 79 82
Aczel, P. [7] 79
Aczel, P., Aczel, Hinman [8] 204
Aczel, P., Richter, Aczed [135] 83
Adequate 144 158
Admissibility in set-recursion 187 188
Admissible collapse 163
Admissible ordinal 109 137 160
Admissible ordinal,  -admissible 129 -admissible 129
Admissible ordinal, F-admissible 130
Admissible ordinal, next-admissible 124 125
Admissible prewellordering 110 113
Admissible set 109
Admissible set, next admissible 124 125
Admissible set, non-transitive 29
Associate 205
Barendregt, H. [9] 203
Barwise, K.J. 81
Barwise, K.J. [10] 124
Barwise, K.J. [11] 82 109 110 126
Barwise, K.J. [13] 82
Barwise, K.J., Barwise, Gandy, Moschovakis [14] 124
Basis results 204
Bergstra, J. [15] 139 207
Blocking procedure 153
Cenzer, D. [18] 83
Characterization theorem, admissible prewellorderings 121
Characterization theorem, normal theories 180
Characterization theorem, Spector theories 129
Code set 20
Coding scheme 90
Computation domain 19 30 90 111
Computation set 20
Computation structure 44
Computation theory 8 44
Computation theory,  -Mahlo 128 180 -Mahlo 128 180
Computation theory,  -resolvable 111 -resolvable 111
Computation theory, equivalence of 34 48 76
Computation theory, extension 34 48
Computation theory, infinite 112
Computation theory, normal 168
Computation theory, p-normal 66
Computation theory, precomputation 22 30
Computation theory, regular 52
Computation theory, s-normal 58
Computation theory, set-recursion 183
Computation, convergent 94
Computation, derivation 57
Computation, deterministic 57
Computation, divergent 94
Computation, immediate subcomputation 32 47 94
Computation, length of computation 32 44 46 65 94 183
Computation, subcomputation 32 38 44 47 54 57 94 183
Computation, subcomputation tree 33 38 95 183
Continuous functional 204
Countable functional 204
Countable functional, associate 205
Countable functional, fan functional 206
Countable functional, Kleene computable 206
Countable functional, recursively countable 206
Cut-elimination lemma 57
Deficiency set 148
Definition by cases 21
Degree 140 150 157
Density theorem 157
Descriptive set theory 79 203
Determinacy 158
Devlin, K.J. [19] 182 183
Diagonalization operator for inductive definitions 204
Driscoll, G.C., Jr. [21] 145
Effective discontinuity 205
Enumeration, 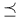 enumeration 141 enumeration 141
Enumeration, enumeration property 13
Envelope 73 171
Envelope, extended 73
Envelope, S-envelope 171
Ershov, Y.L. [22] 207
Ershov, Y.L. [23] 207
Faithful representation theorem 58
Fap C-computable 6
Fap CS-computable 6
Fap S-computable 5
Fap-computable 4
Fattening lemma 127 180
Feferman, S. [24] 136
Feferman, S. [25] 12 14 207
Fenstad, J.E. [26] 15 124
Fenstad, J.E. [27] 15
Fenstad, J.E. [28] 15
Fenstad, J.E. [29] 15
Fenstad, Normann [32] 203
Finite,  -finite 159 -finite 159
Finite,  -finite 52 66 -finite 52 66
Finite, invariantly finite 162
Finite, strongly  -finite 66 -finite 66
Finite, weakly  -finite 66 -finite 66
First recursion theorem 40 48 75 95
Fixed-point operator 7 11
Fixed-point property 13
Fixed-point theorem 25
Forcing 137
Friedman, H. [33] 3 42
Friedman, H. [34] 4 5
Friedman, S.D. [35] 159 160
Friedman, S.D. [36] 160
Friedman, Sacks [31] 159
Function,  -computable 21 -computable 21
Function, partial multiple-valued (pmv) 20
Functional, composition 22
Functional, consistent 21
Functional, monotone 13 95
Functional, partial multiple-valued (pmv) 21
Functional, partial recursive 95
Functional, permutation 22
Functional, strongly  -computable 39 -computable 39
Functional, uniformly weakly  -computable 46 -computable 46
Functional, weakly  -computable 21 44 -computable 21 44
Functional, weakly partial recursive 95
Gandy fixed-point theorem 110
Gandy selection theorem (3.1.6) 65 68
Gandy — Spector theorem 99 123 190 191
Gandy, R.O. [38] 65 204
Gandy, R.O. [39] 79 80
Gandy, R.O. [40] 182
Gandy, R.O., Barwise, Gandy, Moschovakis [41] 124
Gandy, R.O., Gandy, Hyland [42] 207
Gandy, R.O., Gandy, Sacks [43] 136
Gap phenomena 204
Gordon, C.E. [45] 110
Gregory, J. [46] 109
Grilliot selection theorem 90 100 184
Grilliot, T.J. [48] 100
Grilliot, T.J. [49] 80 83 87 88
Grilliot, T.J. [50] 205
Grilliot, T.J. [51] 203
Gurrik, P.K. [52] 183 189
Harrington, L.A. 77 79 158 204
Harrington, L.A. [53] 169 171 182 190 194 202 204
Harrington, L.A. [54] 204
Harrington, L.A., Harrington, Kechris [56] 134
Harrington, L.A., Harrington, Kechris [57] 83 87
Harrington, L.A., Harrington, Kechris, Simpson [58] 134
Harrington, L.A., Harrington, MacQueen [55] 90 100
| Hereditarily consistent functionals 11
hierarchies 204
Hinman, P.G. [59] 67
Hinman, P.G. [60] 207
Hinman, P.G. [61] 204
Hinman, P.G., Aczel, Hinman [8] 204
Hinman, P.G., Hinman, Moschovakis [62] 181
Hodges, W. [63] 203
Hyland, J.M.E. [64] 207
Hyland, J.M.E. [65] 207
Hyland, J.M.E. [66] 207
Hyland, J.M.E. [67] 207
Hyland, J.M.E., Gandy, Hyland [42] 207
Hyperanalytic 90
Hyperprojective theory 181
Hyperregular 146
Imbedding theorem 126
Inadmissible ordinal, strongly 160
Inadmissible ordinal, weakly 160
Inadmissible theory 159
Induction algebra 14
Inductive definability 7 79
Inductive definability, 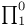 80 80
Inductive definability, 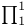 monotone 81 monotone 81
Inductive definability, 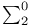 87 87
Inductive definability, 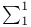 monotone 82 monotone 82
Inductive definability, fixed-points of 79
Inductive definability, monotone 79
Inductive definability, ordinal of 79
Inductive definability, positive 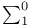 80 80
Inductive definability, positive elementary 81
Inductive definability, stages of 79
Inductive relations, C-coinductive 80
Inductive relations, C-hyperdefinable 80
Inductive relations, C-inductive 80
Infinite computation theory 112
Iteration property 22 45
Jensen, R.B. [70] 136
Jensen, R.B. [71] 182 183
Jensen, R.B., Jensen, Karp [72] 109 182
Jump 149
Jump, a-jump 195
Karp, C., Jensen, Karp [72] 109 182
Kechris, A.S. [74] 134 169 190 204
Kechris, A.S. [75] 79
Kechris, A.S. [76] 106 169 203 204
Kechris, A.S., Harrington, Kechris [56] 134
Kechris, A.S., Harrington, Kechris [57] 83 87
Kechris, A.S., Harrington, Kechris, Simpson [58] 134
Kechris, A.S., Kechris, Moschovakis [77] 12 13
Kierstead, D.P. 203
Kleene recursion in higher types (S1-S9) 67 106
Kleene recursion in higher types (S1-S9) and set-recursion 189 192
Kleene, S.C. [78] 41
Kleene, S.C. [79] 65 122
Kleene, S.C. [80] 65 122
Kleene, S.C. [81] 65 122
Kleene, S.C. [82] 207
Kleene, S.C. [83] 3 42 65 67 94 206
Kleene, S.C. [84] 123
Kleene, S.C. [86] 203
Kolaitis, P.G. [87] 82
Kreisel, G. [88] 207
Kreisel, G. [89] 52 65
Kreisel, G. [90] 145
Kreisel, Sacks [91] 52 65 123
Kripke, S. 109
Kripke, S. [92] 123
Lambda-calculus 42 203
Lavori, P. [95] 204
Locally of type I 188
Louveau, A. [96] 203
Louveau, A. [97] 203
Maass, W. [100] 160 163
Maass, W. [101] 159
Maass, W. [102] 161 163
MacQueen, D.B. [98] 100 182 190
MacQueen, D.B., Harrington, MacQueen [55] 90 100
Malcev, A.I. [99] 10
Mapping 21
Minimum operator ( -operator) 27 -operator) 27
Mitschke, G. [104] 203
Moldestad, J. 60
Moldestad, J. [105] 7 11 90 99 100 106 134 135 168 169 171 203 204
Moldestad, J. [106] 29
Moldestad, J., Moldestad, Normann [107] 204
Moldestad, J., Moldestad, Stoltenberg-Hansen, Tucker [108] 4 5 6 8
Moldestad, J., Moldestad, Stoltenberg-Hansen, Tucker [109] 4 6 9
Moldestad, Tucker [110] 14
Moschovakis, Y.N. 182
Moschovakis, Y.N. [111] 90
Moschovakis, Y.N. [112] 3 42 110 124
Moschovakis, Y.N. [113] 3 42 43 46 48 52 65 72 110 121 122
Moschovakis, Y.N. [114] 75 90
Moschovakis, Y.N. [115] 74 79 81 82 87 124
Moschovakis, Y.N. [116] 79 83 84
Moschovakis, Y.N. [117] 12 14 79
Moschovakis, Y.N. [118] 79 106 203
Moschovakis, Y.N., Barwise, Gandy, Moschovakis [14] 124
Moschovakis, Y.N., Hinman, Moschovakis [62] 181
Moschovakis, Y.N., Kechris, Moschovakis [77] 12 13
Normal function 130
Normal list 97
Normal type-2 functional 127
Normann, D. 184 202
Normann, D. [121] 137
Normann, D. [122] 182 190
Normann, D. [123] 207
Normann, D. [124] 182 184 189
Normann, D. [125] 202
Normann, D. [126] 204
Normann, D. [127] 202
Normann, D. [128] 207
Normann, D. [129] 207
Normann, D., Fenstad, Normann [32] 203
Normann, D., Moldestad, Normann [107] 204
Normann, D., Normann, Stoltenberg-Hansen [130] 158
Normann, D., Normann, Wainer [131] 207
Nyberg, A. [132] 110
Operator,  -computable 84 -computable 84
Operator, adequate class 87
Operator, typical non-monotone class 83
Ordered n-tuple 31
Ordinal,  -Mahlo 130 -Mahlo 130
Ordinal, subconstructive 172
p-normal 66
Pairing structure 30
Parametrization,  -parametrization 13 -parametrization 13
Parametrization, 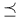 -parametrization 141 -parametrization 141
Parametrization, Spector classes 74
Partial recursive function 93 94
Platek, R.A. 109
Platek, R.A. [133] 7 11 124
Plus-one theorem 138
Plus-two theorem 171
Post, E. 80
Precomputation theory 22 30
Predecessor function 27
Prewellordering 65 85
Prewellordering, length of 111
Prime computable 3
Prime computation set 32 46
Primitive recursion 28 91
Primitive recursive set function 182
Priority argument 140 156 182 202
Projectible 142
Projectum 143
Projectum, r.e.-projectum 144
Quantifier, Monotone 67 82
Reducibility relations 140
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -admissible
-admissible 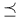 enumeration
enumeration  -finite
-finite 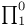
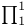 monotone
monotone 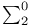
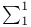 monotone
monotone 
 -operator)
-operator)  -parametrization
-parametrization