|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Fenstad J.E. — General recursion theory: An axiomatic approach |
|
|
 |
| Предметный указатель |
Reducibility relations, 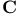 -reflection 84 -reflection 84
Reducibility relations,  -computable 144 -computable 144
Reducibility relations,  -definable, -definable,  145 145
Reducibility relations,  -semicomputable 144 -semicomputable 144
Reducibility relations, many-one reducible 149
Reducibility relations, set recursion 194
Reducibility relations, weakly  -computable 144 -computable 144
Reducibility relations, weakly  -semicomputable 144 -semicomputable 144
Reflection principles 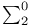 -reflection 80 -reflection 80
Reflection principles in higher types 204
Reflection principles in higher types, compactness 170
Reflection principles in higher types, further reflection 169
Reflection principles in higher types, simple reflection 169
register 4
Register, algebra 6
Register, counting 6
Regular set 146
Regular set theorem 147 148
Relations,  -computable 25 50 69 -computable 25 50 69
Relations,  -semicomputable 25 50 69 -semicomputable 25 50 69
Relations, 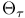 -computable 129 -computable 129
Relations, 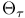 -semicomputable 129 -semicomputable 129
Representation theorem for Spector classes 79
Representation theorem for Spector theories 77
Resolvable structures 110
Resolvable structures,  -resolvable 111 -resolvable 111
Richter, W. [134] 80
Richter, W., Richter, Aczel [135] 83
Rudimentary set function 182 183
S-normal 58
Sacks, G.E. 169 202
Sacks, G.E. [138] 150
Sacks, G.E. [139] 157
Sacks, G.E. [140] 145 147
Sacks, G.E. [141] 136
Sacks, G.E. [142] 135
Sacks, G.E. [143] 169 171
Sacks, G.E. [144] 159 194 202
Sacks, G.E., Friedman, Sacks [37] 159
Sacks, G.E., Gandy, Sacks [43] 136
Sacks, G.E., Kreisel, Sacks [91] 52 65 123
Sasso, L.P. [145] 42
Schwichtenberg, H., Schwichtenberg, Wainer [146] 204
Schwichtenberg, Wainer [146] 204
Search computable 3
Second recursion theorem 95 96
Section 73 171
Section, extended 72
Selection principles, computation theories 51
Selection principles, higher types (Grilliot selection) 100
Selection principles, infinite theories 112 142
Selection principles, p-normal theories (Gandy selection) 68
Selection principles, precomputation theories 26
Selection principles, Spector classes 74
Set-recursion and admissibility 187 188
Set-recursion, set-recursive closure 185
Set-recursion, set-recursive function 182 183
Set-recursion, set-recursive relative to 185
| Shepherdson, J.C. [148] 4
Shoenfield, J.R. [149] 204
Shore, R. [150] 150 157
Shore, R. [151] 157
Shore, R. [152] 109 140 145 150
Simple representation theorem 35
Simpson, S.G. [153] 147
Simpson, S.G. [154] 150
Simpson, S.G. [155] 158
Simpson, S.G. [156] 109 183
Simpson, S.G., Harrington, Kechris, Simpson [58] 134
Singlevalued theory 29
Spector 2-classes 106
Spector Class 73
Spector class, coding scheme 74
Spector class, normed 74
Spector class, parametrizable 74
Spector class, reduction property 74
Spector class, selection principle 74
Spector class, separation property 74
Spector theory 73
Spector theory,  -Mahlo 128 -Mahlo 128
Spector theory, equivalence of 76
Spector theory, weak Spector theory 87
Spector, C. 65 72
Spector, C. [158] 122
Spector, C. [159] 123
Spector, C. [160] 123
Spector, C. [161] 81 123
Spectrum 187
Splitting theorem 150
Stoltenberg-Hansen, V. 157 161
Stoltenberg-Hansen, V. [162] 148 150 151
Stoltenberg-Hansen, V. [163] 122 146 150 151
Stoltenberg-Hansen, V. [164] 147
Stoltenberg-Hansen, V. [165] 160
Stoltenberg-Hansen, V., Moldestad, Stoltenberg-Hansen, Tucker [108] 4 5 6 8
Stoltenberg-Hansen, V., Moldestad, Stoltenberg-Hansen, Tucker [109] 4 6 9
Stoltenberg-Hansen, V., Normann, Stoltenberg-Hansen [130] 158
Strong, H.R. [166] 3 42
Successor function 28 30
Superjump 204
Tait, W. 207
Tame approximation 153
Term evaluation function 9
Troelstra, A.S. [167] 207
Tucker, J.V. [168] 10
Tucker, J.V., Moldestad, Stoltenberg-Hansen, Tucker [108] 4 5 6 8
Tucker, J.V., Moldestad, Stoltenberg-Hansen, Tucker [109] 4 6 9
Tucker, J.V., Moldestad, Tucker [110] 14
Turing, A.M. 3
type structure 205
Universal function 34
Wagner, E.G. [169] 3 42
Wainer, S.S. [170] 204
Wainer, S.S., Normann, Wainer [131] 207
Wang, H. [171] 123
Weak definition by cases 59
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



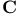 -reflection
-reflection  -computable
-computable 
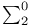 -reflection
-reflection 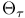 -computable
-computable