Pade approximation, convergence of II 80
Pade approximation, table II 66 75—77
Painleve's transcendent II 89
Parabolic cylinder functions I 135 212
Pi ( ), asymptotic expansion for I 35 36 ), asymptotic expansion for I 35 36
Pi ( ), value of II 292 ), value of II 292
Polynomial approximation see "Approximation"
Polynomials see "Bessel orthogonal etc."
Power series and ratio of power series, Pade approximation for II 76
Powers of z, expansions for see "Expansion"
Psi ( )-function or logarithmic derivative of the gamma function, approximation see "Approximation" )-function or logarithmic derivative of the gamma function, approximation see "Approximation"
Psi ( )-function or logarithmic derivative of the gamma function, asymptotic expansion I 33 )-function or logarithmic derivative of the gamma function, asymptotic expansion I 33
Psi ( )-function or logarithmic derivative of the gamma function, definition and elementary properties I 12 13 )-function or logarithmic derivative of the gamma function, definition and elementary properties I 12 13
Psi ( )-function or logarithmic derivative of the gamma function, expansion see "Expansion" )-function or logarithmic derivative of the gamma function, expansion see "Expansion"
Psi ( )-function or logarithmic derivative of the gamma function, integral representations I 13—15 28 )-function or logarithmic derivative of the gamma function, integral representations I 13—15 28
Psi ( )-function or logarithmic derivative of the gamma function, power series expansion I 26 )-function or logarithmic derivative of the gamma function, power series expansion I 26
R see "Recurrence formula"
Rational approximation see "Approximation"
Recurrence formula for 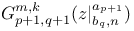 and family of functions which satisfy the same differential equation as does the above function II 156 and family of functions which satisfy the same differential equation as does the above function II 156
Recurrence formula for 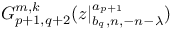 and family of functions which satisfy the same differential equation as does the above function II 153—159 and family of functions which satisfy the same differential equation as does the above function II 153—159
Recurrence formula for 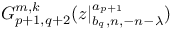 and family of functions which satisfy the same differential equation as does the above function, a special case II 26 and family of functions which satisfy the same differential equation as does the above function, a special case II 26
Recurrence formula for 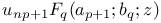 with all parameters as in the preceding example and family of functions which satisfy the same differential equation as does the above function II 156 157 with all parameters as in the preceding example and family of functions which satisfy the same differential equation as does the above function II 156 157
Recurrence formula for ![$[u_{n}/(n+\lambda)_{n}] _{p+1}F_{q+1}(a_{p+1};b_{q},\lambda+1+2n;z)$](/math_tex/c00e2680340a135619d38f10ef23076d82.gif) , , 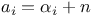 , i=1,2,...,p+1, , i=1,2,...,p+1, 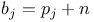 , j=1,2,...,q, , j=1,2,...,q, 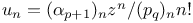 and family of functions which satisfy the same differential equation as does the above function II 157 158 and family of functions which satisfy the same differential equation as does the above function II 157 158
Recurrence formula for ![$[u_{n}/(n+\lambda)_{n}] _{p+1}F_{q+1}(a_{p+1};b_{q},\lambda+1+2n;z)$](/math_tex/c00e2680340a135619d38f10ef23076d82.gif) , , 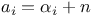 , i=1,2,...,p+1, , i=1,2,...,p+1, 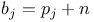 , j=1,2,...,q, , j=1,2,...,q, 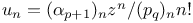 and family of functions which satisfy the same differential equation as does the above function, special case p=0, q=1 II 35 37 and family of functions which satisfy the same differential equation as does the above function, special case p=0, q=1 II 35 37
Recurrence formula for ![$[u_{n}/(n+\lambda)_{n}] _{p+1}F_{q+1}(a_{p+1};b_{q},\lambda+1+2n;z)$](/math_tex/c00e2680340a135619d38f10ef23076d82.gif) , , 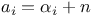 , i=1,2,...,p+1, , i=1,2,...,p+1, 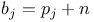 , j=1,2,...,q, , j=1,2,...,q, 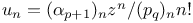 and family of functions which satisfy the same differential equation as does the above function, special case p=2, q=1 II 34 48 159 and family of functions which satisfy the same differential equation as does the above function, special case p=2, q=1 II 34 48 159
Recurrence formula for ![$[u_{n}/(n+\lambda)_{n}] _{p+1}F_{q+1}(a_{p+1};b_{q},\lambda+1+2n;z)$](/math_tex/c00e2680340a135619d38f10ef23076d82.gif) , , 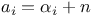 , i=1,2,...,p+1, , i=1,2,...,p+1, 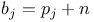 , j=1,2,...,q, , j=1,2,...,q, 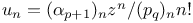 and family of functions which satisfy the same differential equation as does the above function, special case p=3, q=2 II 158 and family of functions which satisfy the same differential equation as does the above function, special case p=3, q=2 II 158
Recurrence formula for ![$[u_{n}/(n+\lambda)_{n}] _{p+1}F_{q+1}(a_{p+1};b_{q},\lambda+1+2n;z)$](/math_tex/c00e2680340a135619d38f10ef23076d82.gif) , , 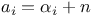 , i=1,2,...,p+1, , i=1,2,...,p+1, 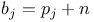 , j=1,2,...,q, , j=1,2,...,q, 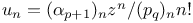 and family of functions which satisfy the same differential equation as does the above function, special case p=q=1 II 35 and family of functions which satisfy the same differential equation as does the above function, special case p=q=1 II 35
Recurrence formula for 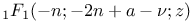 II 190 191 II 190 191
Recurrence formula for 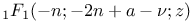 , , 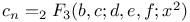 ; b=a-n, ; b=a-n, 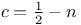 , , 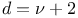 , e=a-2n, , e=a-2n, 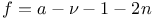 , a=0 or 1 II 82 193 , a=0 or 1 II 82 193
Recurrence formula for 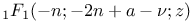 , , 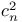 , , 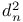 , , 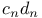 II 193 II 193
Recurrence formula for 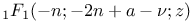 , , 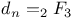 as above with b = -n, as above with b = -n, 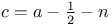 , , 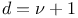 , e=a-1-2n, , e=a-1-2n, 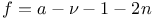 , a=0 or 1 II 82 193 , a=0 or 1 II 82 193
Recurrence formula for 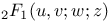 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=-n+1/x, w=1-a+1/x, z=x II 181 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=-n+1/x, w=1-a+1/x, z=x II 181
Recurrence formula for 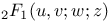 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=-n+a- where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=-n+a- , w=-2n+a- , w=-2n+a- , z=-z II 177 , z=-z II 177
Recurrence formula for 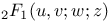 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=-n- where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=-n-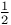 , w= , w=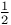 , z=z II 185 , z=z II 185
Recurrence formula for 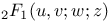 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=x-n, w=x+1-a, z=x II 180 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=x-n, w=x+1-a, z=x II 180
Recurrence formula for 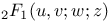 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=1, v=m+ where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=1, v=m+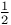 +b, w=m+ +b, w=m+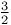 +b, z=-x II 276 +b, z=-x II 276
Recurrence formula for 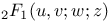 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=1-n, v=-n+ where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=1-n, v=-n+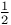 , w= , w=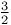 , z=z II 185 , z=z II 185
Recurrence formula for 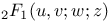 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=a-n, v=a-n-1/x, w=1+a-1/x, z=x II 181 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=a-n, v=a-n-1/x, w=1+a-1/x, z=x II 181
Recurrence formula for 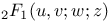 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=a-n, v=a-x-n, w=1+a-x, z=x II 180 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=a-n, v=a-x-n, w=1+a-x, z=x II 180
Recurrence formula for 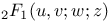 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=n+ where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=n+ , v= , v= , w=n+1, z=z II 36 , w=n+1, z=z II 36
Recurrence formula for 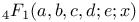 , a=-m, b=m+1+ , a=-m, b=m+1+ , c=m+ , c=m+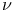 + + , d=1-m- , d=1-m-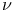 , e= , e=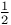 + + II 232 II 232
Recurrence formula for 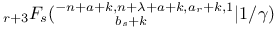 as a function of k II 152 as a function of k II 152
Recurrence formula for Bernoulli polynomials, generalized I 20 22 35
Recurrence formula for coefficients in the expansion of 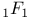 in series of the Bessel functions in series of the Bessel functions 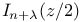 II 48 II 48
Recurrence formula for coefficients in the expansions of the functions named below in series of Chebyshev polynomials of the first kind, 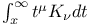 II 241 II 241
Recurrence formula for coefficients in the expansions of the functions named below in series of Chebyshev polynomials of the first kind,  -function or confluent hypergeometric function II 26 239 -function or confluent hypergeometric function II 26 239
Recurrence formula for coefficients in the expansions of the functions named below in series of Chebyshev polynomials of the first kind, 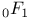 II 35 235—238 II 35 235—238
Recurrence formula for coefficients in the expansions of the functions named below in series of Chebyshev polynomials of the first kind, 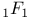 II 35 II 35
Recurrence formula for coefficients in the expansions of the functions named below in series of Chebyshev polynomials of the first kind, 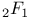 II 34 II 34
| Recurrence formula for Jacobi polynomial, extended, 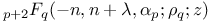 and family of functions which satisfy same differential equation as does the above polynomial II 134—148 156 and family of functions which satisfy same differential equation as does the above polynomial II 134—148 156
Recurrence formula for Jacobi polynomial, extended, 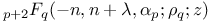 and family of functions which satisfy same differential equation as does the above polynomial, special case p=0, q=1 II 170—172 177 179 and family of functions which satisfy same differential equation as does the above polynomial, special case p=0, q=1 II 170—172 177 179
Recurrence formula for Jacobi polynomial, extended, 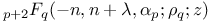 and family of functions which satisfy same differential equation as does the above polynomial, special case p=0, q=2 II 229 230 and family of functions which satisfy same differential equation as does the above polynomial, special case p=0, q=2 II 229 230
Recurrence formula for Jacobi polynomial, extended, 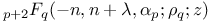 and family of functions which satisfy same differential equation as does the above polynomial, special case p=0, q=3 II 449 and family of functions which satisfy same differential equation as does the above polynomial, special case p=0, q=3 II 449
Recurrence formula for Jacobi polynomial, extended, 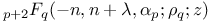 and family of functions which satisfy same differential equation as does the above polynomial, special case p=1, q=2 II 48 147 and family of functions which satisfy same differential equation as does the above polynomial, special case p=1, q=2 II 48 147
Recurrence formula for Jacobi polynomial, extended, 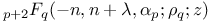 and family of functions which satisfy same differential equation as does the above polynomial, special case p=1, q=3 II 146 and family of functions which satisfy same differential equation as does the above polynomial, special case p=1, q=3 II 146
Recurrence formula for Jacobi polynomial, extended, 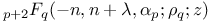 and family of functions which satisfy same differential equation as does the above polynomial, special case p=2, q=3 II 145 146 and family of functions which satisfy same differential equation as does the above polynomial, special case p=2, q=3 II 145 146
Recurrence formula for Jacobi polynomial, extended, 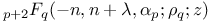 and family of functions which satisfy same differential equation as does the above polynomial, special case p=q=0 II 190—192 and family of functions which satisfy same differential equation as does the above polynomial, special case p=q=0 II 190—192
Recurrence formula for Jacobi polynomial, extended, 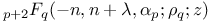 and family of functions which satisfy same differential equation as does the above polynomial, special case p=q=1 II 197 198 and family of functions which satisfy same differential equation as does the above polynomial, special case p=q=1 II 197 198
Recurrence formula for Laguerre polynomial, extended, 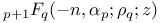 and family of functions which satisfy same differential equation as does the above polynomial II 143—145. and family of functions which satisfy same differential equation as does the above polynomial II 143—145.
Recurrence formula for Laguerre polynomial, extended, 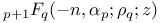 and family of functions which satisfy same differential equation as does the above polynomial, special case p=0, q=1 II 198—201 and family of functions which satisfy same differential equation as does the above polynomial, special case p=0, q=1 II 198—201
Recurrence formula for Laguerre polynomial, extended, 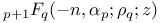 and family of functions which satisfy same differential equation as does the above polynomial, special case p=1, q=2 II 147 and family of functions which satisfy same differential equation as does the above polynomial, special case p=1, q=2 II 147
Recurrence formula for Pade approximations II 78 88 133 see
Recurrence formula for polynomials in polynomial and rational approximations to generalized hypergeometric functions II 134—166 see
Recurrence formulas, use of in computation I 317—319 325—329 II 26—28 159—166 282—285
Representation formulas for polynomials II 139 140 142 144
RF see "Rational function"
RFP see "Rational function which is also a Pade approximation"
Riccati differential equations II 77—91
Saalschuetz's formula I 103
Selected points, method of II 69
Sine and cosine I 23 39 210 see "Expansion"
Sine and cosine integrals I 135 221—223 227 II 27 see "Expansion"
Stokes phenomenon I 128 199
Struve functions see also "Approximation" "Expansion"
Struve functions, asymptotic expansion I 219
Struve functions, definition I 217
Struve functions, difference-differential properties I 218
Struve functions, expressed as a G-function I 227 233
Struve functions, integrals involving I 165 220 II 40
Tables (of) Bernoulli polynomials and numbers I 19 20 34
Tables (of) coefficients for expansion of functions in series of Chebyshev polynomials of the first kind and for approximations of functions in the form of polynomials and rational functions II 282—452 see "Expansion"
Tables (of) mathematical constants II 292 293
Tangent and cotangent I 23 see "Expansion"
Tangent and cotangent, inverse of I 38 40 210
tr see "Trapezoidal or modified trapezoidal rule integration formula"
Trapezoidal-type integration formulas II 214—226
Ultraspherical polynomial I 273 279
Vandermonde's theorem I 99
Watson's formula I 104
Watson's lemma I 4—7
Weber function see "Anger — Weber"
Whipple's formula II 104
Whittaker functions see also "Hypergeometric function confluent"
Whittaker functions, definition I 134
Whittaker functions, expressed as G-function I 225 226 228 231 233 234
Wronskians I 84 85 124 II 101
Y-transform I 165
Zeta-function (Riemann) I 27 II 287 293 306
|
 |
|
О проекте
|
|
О проекте



 ), asymptotic expansion for
), asymptotic expansion for  )-function or logarithmic derivative of the gamma function, approximation
)-function or logarithmic derivative of the gamma function, approximation 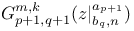 and family of functions which satisfy the same differential equation as does the above function
and family of functions which satisfy the same differential equation as does the above function 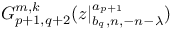 and family of functions which satisfy the same differential equation as does the above function
and family of functions which satisfy the same differential equation as does the above function 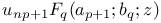 with all parameters as in the preceding example and family of functions which satisfy the same differential equation as does the above function
with all parameters as in the preceding example and family of functions which satisfy the same differential equation as does the above function ![$[u_{n}/(n+\lambda)_{n}] _{p+1}F_{q+1}(a_{p+1};b_{q},\lambda+1+2n;z)$](/math_tex/c00e2680340a135619d38f10ef23076d82.gif) ,
, 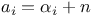 , i=1,2,...,p+1,
, i=1,2,...,p+1, 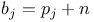 , j=1,2,...,q,
, j=1,2,...,q, 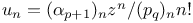 and family of functions which satisfy the same differential equation as does the above function
and family of functions which satisfy the same differential equation as does the above function 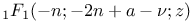
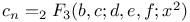 ; b=a-n,
; b=a-n, 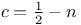 ,
, 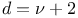 , e=a-2n,
, e=a-2n, 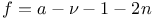 , a=0 or 1
, a=0 or 1 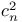 ,
, 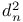 ,
, 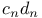
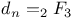 as above with b = -n,
as above with b = -n, 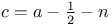 ,
, 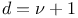 , e=a-1-2n,
, e=a-1-2n, 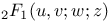 where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=-n+1/x, w=1-a+1/x, z=x
where u, v, w, and z are given in the following, a=0 or 1, b=0 or 1/2, u=-n, v=-n+1/x, w=1-a+1/x, z=x  , w=-2n+a-
, w=-2n+a- , z=-z
, z=-z 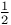 , w=
, w=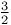 +b, z=-x
+b, z=-x  , v=
, v=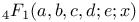 , a=-m, b=m+1+
, a=-m, b=m+1+ , c=m+
, c=m+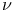 +
+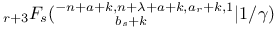 as a function of k
as a function of k 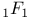 in series of the Bessel functions
in series of the Bessel functions 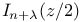
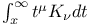
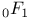
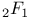
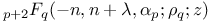 and family of functions which satisfy same differential equation as does the above polynomial
and family of functions which satisfy same differential equation as does the above polynomial 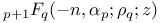 and family of functions which satisfy same differential equation as does the above polynomial
and family of functions which satisfy same differential equation as does the above polynomial