|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kollar J., Mori S. — Birational geometry of algebraic varieties |
|
|
 |
| Предметный указатель |
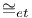 etale equivalence 149 etale equivalence 149
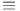 , numerical equivalence 4 , numerical equivalence 4
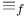 , numerical f-equivalence 5 , numerical f-equivalence 5
$(L_1…L_d Z), intersection number 29
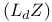 , d-fold intersection number 29 , d-fold intersection number 29
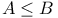 , A - B is effective 4 , A - B is effective 4
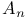 , a type of a Du Val point 122 , a type of a Du Val point 122
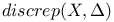 52 52
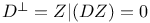 19 19
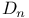 , a type of a Du Val point 122 , a type of a Du Val point 122
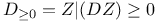 19 19
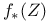 , the birational transform of Z by f 5 , the birational transform of Z by f 5
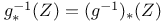 5 5
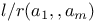 , a , a 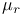 -action 171 -action 171
![$L^{[i]}$](/math_tex/5959c180e5c6b9e2cbdc6fe484fa0d7882.gif) , the double dual of , the double dual of 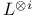 64 64
![$L^{[i]}$](/math_tex/5959c180e5c6b9e2cbdc6fe484fa0d7882.gif) , the double dual of , the double dual of 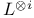 64 64
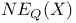 19 19
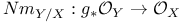 154 154
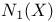 , the space of 1-cycles of X modulo numerical equivalence 18 , the space of 1-cycles of X modulo numerical equivalence 18
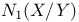 45 45
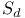 , Serre’s condition 153 , Serre’s condition 153
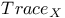 for for 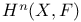 180 180
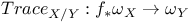 185 185
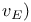 , the valuation at E 218 , the valuation at E 218
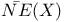 46 46
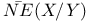 , the closure of NE(X) 19 , the closure of NE(X) 19
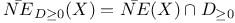 19 19
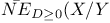 ) 46 95 ) 46 95
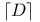 , the round up of divisor D 5 , the round up of divisor D 5
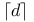 |, the round up of |, the round up of 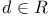 5 5
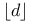 , the round down of , the round down of 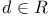 5 5
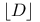 , the round down of divisor D 5 , the round down of divisor D 5
 -Cartier, divisor 4 -Cartier, divisor 4
 -Divisor 4 -Divisor 4
 -factorial 4 47 158 -factorial 4 47 158
 -factorial, globally analytically 47 -factorial, globally analytically 47
 -factorial, locally analytically 47 -factorial, locally analytically 47
 -Factorialization 195 -Factorialization 195
 -Fano fibration 46 -Fano fibration 46
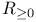 , the set of real numbers , the set of real numbers 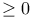 6 6
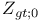 , the set of positive integers 6 , the set of positive integers 6
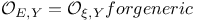 \xi\in E$ 50 \xi\in E$ 50
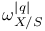 , the double dual of , the double dual of 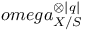 164 164
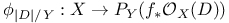 94 94
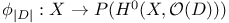 68 68
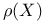 , the Picard number of X 19 , the Picard number of X 19
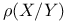 , relative Picard number 45 , relative Picard number 45
 , linear equivalence 4 , linear equivalence 4
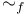 , linear f-equivalence 5 , linear f-equivalence 5
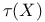 , Tyurina number 129 , Tyurina number 129
(-l)-Curve 8
(K + D)-Flip 99
(K + D)-Flipping contraction 99 189
1-Complement 221
1-Cycle 11 18
1-Cycle, effective 18
1-Cycle, relative 45
:=, is defined by 6
Abelian surface 22
Abundance conjecture 81
Adjunction 173
Adjunction, formula 21 182
Adjunction, inversion of 173 174
Algebra, symbolic power 189
Algebraic equivalence 10 11
Algebraic function 148
Algebraic space 148
Algebraic valuation 50
Almost all 14
Ample, /- 34 35
Analytic case 47
Analytic singularity type 193
Analytic surface 25
Aut, the automorphism group 165 217
Automorphism 22 165
Basepoint-free theorem 75 78
Basepoint-free theorem, relative 94
Bend and break 9 11
Big 67
Big, /- 94
Bimeromorphic map 6
Birational map 6
Birational transform 5
Blow up, symbolic 199
Blow up, weighted 142 143 167 170
Branch 114
Bundle, canonical 47
Bundle, conic 28
Bundle, lattice 10
C, a type of an extremal ray 28
Calabi — Yau threefold 239
Canonical 42 56 165 238
Canonical bundle 47
Canonical bundle formula 52
Canonical bundle formula, Kodaira’s 49
Canonical divisor 47
Canonical flop 191
Canonical model 107
Canonical model, weak 107
Canonical ring 80 237
Canonical singularity 42
Cartier, 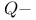 4 4
Castelnuovo’s Theorem 8
cDV, compound Du Val 165 199
Center 51
Chain 114
Chow’s Lemma 32
CM, Cohen — Macaulay 153
Codimension in 159
Codimension of pure 8 70
Cohen — Macaulay, CM 153
Compact complex manifold 13
Compound Du Val, cDV 165
Cone 18
Cone theorem 22 27 38 43 76 81
Cone theorem, relative 95
Cone, example of 21-22
Conic bundle 28
cont, a contraction 25
Contraction 25 46 76
Contraction, (K + D)-flipping 99
Contraction, divisorial 38 43 98
Contraction, extremal 38 43 100
Contraction, Fano 99
Contraction, fiber type 38
Contraction, flipping 43 98
Contraction, flopping 191
Contraction, morphism 27
Contraction, small 38
Contraction, theorem 76
Cover, cyclic 63
Cover, ramified cyclic 64
Cover, unbranched 13
Cover, unramified cyclic 63
Crepant 195
Criterion, Kleiman’s 19 33 35
Criterion, Nakai — Moishezon 31 34
Cubic surface 22
Curve, (-l)- 8
Curve, existence of rational 12 16 22 76 95
Curve, flipped 100
Curve, flipping 100
Curve, multiple 11
Curve, stable 230
Cusp 116
CYCLE 114 115
Cycle, 1- 11 18
Cycle, relative 1- 45
Cyclic cover 63
Cyclic cover, ramified 64
| Cyclic cover, unramified 63
D, a type of an extremal ray 28
Deformation 144
Deformation, miniversal 145
Deformation, space 12 232
Deformation, theory 12
Deformation, versal 145
Degeneration 11
Del Pezzo fibration 28
Del Pezzo surface 22 39
Dimension at 149 150
Dimension, embedding 149 150
Dimension, fiber 9
Dimension, Kodaira 237
discrep(center 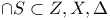 ) 172 ) 172
discrep(center 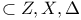 ) 172 ) 172
Discrepancy 50
Discrepancy of a divisor 51 112
Discrepancy of a pair 52
Discrepancy, total 52
Divisor 4
Divisor,  -Cartier 4 -Cartier 4
Divisor, 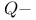 4 4
Divisor, canonical 47
Divisor, effective 4
Divisor, over X 51
Divisor, prime 4
Divisor, simple normal crossing, snc 5
Divisor, support of 4
Divisorial contraction 38 43 98
Divisorial log terminal, dlt 58
Divisorial log terminal, dlt, morphism 208
Dlt, divisorial log terminal 58
Dlt, divisorial log terminal, morphism 208
Dlt, divisorial log terminal, numerically 112
Double dual 64
Du Val, compound, cDV 165
Du Val, singularity 113 143 165
Dual graph 113
Dual graph, extended 114
Dualizing sheaf, 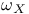 47 180 47 180
e(X) =#{crepant divisor} 198
Easy termination theorem 203
Effective 1-cycle 18
Effective divisor 4
El-5, types of an extremal ray 28 37
Elimination theory 15
Elliptic singularity 138 165
Elliptic threefold 239
Embedding, dimension 149 150
Embedding, minimal 150
En, a type of a Du Val point 122
Endomorphism 13
Endomorphism, Frobenius 14
Equivalence, algebraic 10 11
Equivalence, etale 149
Equivalence, linear 4
Equivalence, linear /- 5
Equivalence, numerical 4 18
Equivalence, numerical f- 5
Etale 148 150
Etale, equivalence 149
Ex(f), the exceptional set of f 5
Example of  simultaneous resolution 128 simultaneous resolution 128
Example of cones 21- 22
Example of degenerations to cones 231
Example of extremal contractions 44
Example of extremal rays 25
Example of f-nef divisors 35
Example of flips 39
Example of Kummer threefolds 37
Example of minimal models 107
Example of non-algebraic varieties 10
Example of non-CM lc singularities 162
Example of simultaneous resolution 132
Example of Tyurina number 129
Exceptional set 5
Existence of  -factorialization 195 -factorialization 195
Existence of flips 189- 191
Existence of flops 192 204
Existence of rational curves 12 16 22 76 95
Existence of semi-stable flips 210 224
Existence of special semi-stable flips 220
Existence of terminalization 195
Extended dual graph 114
Extremal contraction 38 43 100
Extremal contraction, face 18
Extremal contraction, ray 18
Extremal contraction, subcone 18
F, a type of an extremal ray 28
f-equivalence, linear 5
f-equivalence, numerical 5
f-Minimal 106
Face, extremal 18
Factorial, 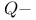 4 47 158 4 47 158
Factorialization, 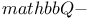 195 195
Family, one-parameter 13
Fano contraction 99
Fano fiber space 44
Fano threefold 239
Fano variety 28
Fiber dimension 9
Fiber space, Fano 44
Fiber type contraction 38
Fibration, 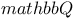 -Fano 46 -Fano 46
Fibration, Del Pezzo 28
Finite kernel 217
Finite quasi- 149 150
Finite sequence is 193 194 203 205 211
Fixed point of an action 40
Flatness, generic 14
Flip 39 41 190 237
Flip, existence of semi-stable 210 224
Flip, existence of special semi-stable 220
Flip, infinite sequence of 193
Flip, semi-stable viii
Flip, sequence of 193
Flip, termination of 193 210 211
Flipped curve 100
Flipping contraction 43 98
Flipping curve 100
FLOP 191
Flop, canonical 191
Flop, existence of 192
Flop, sequence of 194
Flop, terminal 191 192
Flop, termination of 194 203 205
Flopping contraction 191
Fork 114
Formula, adjunction 21
Formula, canonical bundle 52
Formula, Hurwitz 210
Formula, Kodaira’s canonical bundle 49
Fractional part, { } 5
Free, f- 94
Frobenius endomorphism 14
Frobenius morphism 13 14 16
Fujita’s conjecture 238
Function, algebraic 148
Function, regular 148
G-Minimal model 48
GAGA principle 62
General Kodaira vanishing 73
Generic flatness 14
Geometric invariant theory 237
Globally analytically Q-factorial 47
Group, action 47 217
Hensel’s Lemma 125
Hironaka theorem 3 4
Hironaka theorem, weak 3 4
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



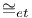 etale equivalence
etale equivalence 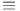 , numerical equivalence
, numerical equivalence 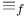 , numerical f-equivalence
, numerical f-equivalence 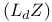 , d-fold intersection number
, d-fold intersection number 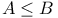 , A - B is effective
, A - B is effective 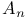 , a type of a Du Val point
, a type of a Du Val point 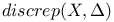
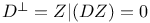
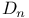 , a type of a Du Val point
, a type of a Du Val point 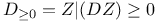
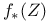 , the birational transform of Z by f
, the birational transform of Z by f 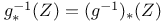
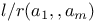 , a
, a 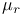 -action
-action ![$L^{[i]}$](/math_tex/5959c180e5c6b9e2cbdc6fe484fa0d7882.gif) , the double dual of
, the double dual of 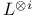
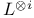
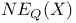
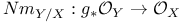
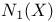 , the space of 1-cycles of X modulo numerical equivalence
, the space of 1-cycles of X modulo numerical equivalence 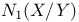
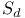 , Serre’s condition
, Serre’s condition 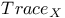 for
for 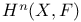
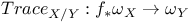
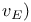 , the valuation at E
, the valuation at E 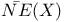
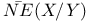 , the closure of NE(X)
, the closure of NE(X) 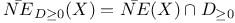
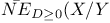 )
) 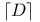 , the round up of divisor D
, the round up of divisor D 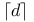 |, the round up of
|, the round up of 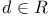
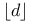 , the round down of
, the round down of 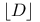 , the round down of divisor D
, the round down of divisor D  -Cartier, divisor
-Cartier, divisor 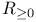 , the set of real numbers
, the set of real numbers 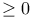
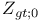 , the set of positive integers
, the set of positive integers 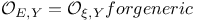 \xi\in E$
\xi\in E$ 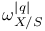 , the double dual of
, the double dual of 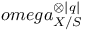
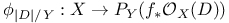
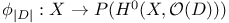
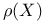 , the Picard number of X
, the Picard number of X 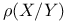 , relative Picard number
, relative Picard number  , linear equivalence
, linear equivalence 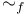 , linear f-equivalence
, linear f-equivalence 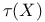 , Tyurina number
, Tyurina number 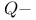
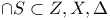 )
) 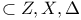 )
) 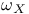
 simultaneous resolution
simultaneous resolution 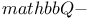
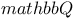 -Fano
-Fano