Transcendental integral function, simple, of given class 91
Transcendental integral function, with unlimited number of zeros over the whole plane, in form of a product 76
Transformation, homographic 512 see
Trasversale 314
Triangle, rectilinear, represented on a half-plane 543
Triangle, separate cases in which representation is complete and uniform 543
Triangle, separate cases in which representation is complete and uniform, curvilinear, represented on a half-plane 555 see
Trigonometrical series, expansion of tertiary periodic functions in 293
Triply-infinite arithmetical system of zeros cannot be possessed by transcendental integral function 91
Triply-periodic uniform functions of a single variable do not exist 205
Triply-periodic uniform functions of a single variable do not exist, example of this proposition 386
Two-sheeted surface, special form of branch-lines for 344
Umgebung 52
Unifacial surface 325
Unifacial Surfaces 325 333
uniform 15
Uniform function of position on a Riemann's surface, has as many zeros as infinities 372
Uniform function of position on a Riemann's surface, most general 369
Uniform function of position on a Riemann's surface, most general, algebraic equation determining 371
Uniform function of position on a Riemann's surface, multiform function becomes 337 343
Uniform function, conditions that a, be an integral of a differential equation of first order not containing the independent variable 471
Uniform function, defined 15
Uniform function, has a unique set of elements in continuation 56
Uniform function, Hermite's sections for integrals of 185
Uniform function, is algebraical polynomial if only singularity be accidental and at infinity 69
Uniform function, is constant everywhere in its region if constant over a line or area 99
Uniform function, is rational algebraical and meromorphic if there be no essential singularity and a finite number of accidental singularities 71
Uniform function, must assume any assigned value 64
Uniform function, must assume any value at an essential singularity 54 94
Uniform function, must have at least one singularity 64
Uniform function, number of zeros of, in an area 63
Uniform function, of one variable, that are periodic 200
Uniform function, of several variables that are periodic 208
Uniform function, transcendental see "Transcendental function"
Uniform function, when the conditions are satisfied, it is either a rational, a simply-periodic, or a doubly-periodic, function 476
Unlimited number of essential singularities, functions possessing Chap. vii
Unlimited number of essential singularities, functions possessing, distributed over the plane 112
Unlimited number of essential singularities, over a finite circle 117
Verzweigungschnitt 339
Verzweigungspunkt 15
Vivanti 92
Von der Muehll 500 576
| von Mangoldt 619 653
Weber 189 511 619 633 637
Weierstrass v vii 14 44 53 54 55 57 74 97 112 238 254 297 311 455 456
Weierstrass's  -function 249 -function 249
Weierstrass's  -function, differential equation satisfied by 266 -function, differential equation satisfied by 266
Weierstrass's  -function, its pseudo-periodicity 259 -function, its pseudo-periodicity 259
Weierstrass's  -function, its quasi-addition-theorem 261 -function, its quasi-addition-theorem 261
Weierstrass's  -function, periodic functions expressed in terms of 260 -function, periodic functions expressed in terms of 260
Weierstrass's  -function, used to construct secondary periodic functions 281 -function, used to construct secondary periodic functions 281
Weierstrass's  -function, used to construct secondary periodic functions, and tertiary periodic functions 288 -function, used to construct secondary periodic functions, and tertiary periodic functions 288
Weierstrass's 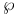 -function 251 -function 251
Weierstrass's 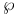 -function is doubly-periodic 252 -function is doubly-periodic 252
Weierstrass's 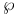 -function is of the second order and the first class 253 -function is of the second order and the first class 253
Weierstrass's 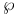 -function, derivatives with regard to the invariants and the periods 265 -function, derivatives with regard to the invariants and the periods 265
Weierstrass's 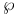 -function, its addition-theorem 262 -function, its addition-theorem 262
Weierstrass's 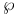 -function, its differential equation 254 -function, its differential equation 254
Weierstrass's 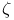 -function 250 -function 250
Weierstrass's 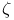 -function, its pseudo-periodicity 255 -function, its pseudo-periodicity 255
Weierstrass's 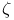 -function, its quasi-addition-theorem 261 -function, its quasi-addition-theorem 261
Weierstrass's 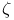 -function, periodic functions expressed in terms of 256 -function, periodic functions expressed in terms of 256
Weierstrass's 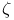 -function, relation between its parameters and periods 257 -function, relation between its parameters and periods 257
Weierstrass's product-form for transcendental integral function, with doubly-infinite arithmetic series of zeros 87
Weierstrass's product-form for transcendental integral function, with infinite number of zeros over the plane 80
Wesentliche singulaere Stelle 53
Weyr 84
Wiener 136
Williamson 20 40
Winding surface, defined 346
Winding surface, portion of, that contains one winding-point is simply connected 948
Winding-point 346
Winding-surface 346
Windungspunkt 15
Witting 93
Zero 16
Zeros of doubly-periodic function, irreducible, are in number equal to the irreducible infinities and the irreducible level points 227
Zeros of doubly-periodic function, irreducible, are in sum are congruent with their sums 228
Zeros of uniform function are isolated points 60
Zeros of uniform function are isolated points, cannot form triply-infinite arithmetical series 98
Zeros of uniform function are isolated points, form of function in vicinity of 61
Zeros of uniform function are isolated points, in an area, number of 61 63 98 72
Zeros of uniform function are isolated points, of transcendental function, when simply-infinite 83
Zeros of uniform function are isolated points, when doubly-infinite 84
Zusammenhaengend, einfach, mehrfach 313 314
|
 |
|
О проекте
|
|
О проекте



 -function
-function 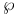 -function
-function 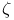 -function
-function