Авторизация
Поиск по указателям
Baker H.F. — Abel's Theorem and the Allied Theory Including The Theory of the Theta Functions
Обсудите книгу на научном форуме Нашли опечатку?
Название: Abel's Theorem and the Allied Theory Including The Theory of the Theta FunctionsАвтор: Baker H.F. Аннотация: Classical algebraic geometry, inseparably connected with the names of Abel, Riemann, Weierstrass, Poincaré, Clebsch, Jacobi and other outstanding mathematicians of the last century, was mainly an analytical theory. In our century the methods and ideas of topology, commutative algebra and Grothendieck's schemes enriched it and seemed to have replaced once and forever the somewhat naive language of classical algebraic geometry. This classic book, written in 1897, covers the whole of algebraic geometry and associated theories. Baker discusses the subject in terms of transcendental functions, and theta functions in particular. Many of the ideas put forward are of continuing relevance today, and some of the most exciting ideas from theoretical physics draw on work presented here.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1897Количество страниц: 684Добавлена в каталог: 25.03.2006Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
292 324 333 516 Abel 90 173 205 206 207ff. 221 225ff. 231 243 246 377 397 657 Abelian functions 236 600 Abelian integrals see Integrals; Abelian matrix 669 Abel’s Abel’s proof of 219 220 Abel’s converse of 222 Abel’s differential equations 225 ff. Abel’s for curves in space 231 Abel’s for factorial functions 397 Abel’s for radical functions 377 Abel’s number of independent equations given by 222ff. Abel’s proof of 213 Abel’s statement of 210 214 Abel’s theorem 207 ff. Addition equation for hyperelliptie theta functions, deduced algebraically 331 ff. Addition for theta functions in general 457 461 472 476 481 513 521 Adjoint expression of rational function by 127 see Integrals Sets Lots. Adjoint number of terms in 128 Adjoint polynomial (or curve), definition of 121 Appell 200 392 Argument and parameter, interchange of 16 185 187 189 191 194 206 Associated, associated system of factorial functions 397 Associated, Forms associated with fundamental integral functions 62 Associated, integrals of second kind associated with integrals of the first kind 193 195 198 532 Automorphic connection with factorial functions 439ff. Automorphic functions, simple ease of 352 ff. Azygetic characteristics 487 497 Azygetic transformation of 542 547 Bacharach 141 Bacharaeh’s modification of Cayley’s theorem for plane curves 141 Bachmann 666 Bam 57 112 Benoist 153 156 222 647 Bertini 137 Biermann 663 Biquadratic see Gopel. Birational transformation of a Riemann surface , by 142 152 Birational transformation of a Riemann surface , does not affect the theory 3 7 Birational transformation of a Riemann surface , for hyperelliptie surface 152 85 Birational transformation of a Riemann surface , number of invariants in 9 144 148 150 Birational transformation of a Riemann surface , of plane curves 11 Birational transformation of a Riemann surface , of surface into itself 658 see Invariants and Birational transformation of a Riemann surface , when 153 Bitangents of a plane curve 381 390 644 646 Bobek 647 Bolza 177 294 296 815 329 842 436 663 Borahardt 340 342 468 Bouquet 90 Branch places see Places. Braunmiihl 486 521 Brill 12 29 134 137 145 149 436 647 Brioschi 296 311 342 448 516 526 668 666 Briot 90 Broch 221 Burkhardt 43 429 436 555 623 663 Burnside 345 373 663 Canonical curve discussed by Klein 159 Canonical equation for a Riemann surface 83 91 103 143 145 152 Canonical integral of the third kind 168 185 189 194 195 Cantor 239 Caspary 474 486 525 Castelnuovo 647 665 Cauchy 600 Cayley 12 137 141 145 165 168 198 222 230 283 296 340 342 374 387 459 540 646 647 650 664 666 668 Cayley’s theorem for plane curves 141 Characteristics, expression of any half-integer characteristic by means of a fundamental system 301 500 502 Characteristics, G 489 490 494 ff. Characteristics, general theory of 486 ff. Characteristics, of a theta function, number of odd and even 251 Characteristics, of radical functions 380 564 Characteristics, period characteristics and theta characteristics 543 564 Characteristics, syzygetic, azygetic 487 Characteristics, tables of half-integer characteristics for 303 305 Characteristics, transformation of 536 542 547 564 568 Characteristics, Weirstrass’s number notation for 570 887 303 ChasUs 187 647 Christoffel 666 Clebsch 131 142 153 156 165 168 183 222 241 244 288 295 392 423 448 544 545 556 578 623 647 Coincidences of a correspondence 645 Column and row see Matrices. Column of periods 571 Complex multiplication of theta functions 629 ff. 639 660 Composition of transformations of theta functions 551 Condition of dimensions 49 Conformal representation 343 356 372 Congruence, meanings of sign of 236 256 261 264 487 Constants, in any transformation of theta functions 620 622 Constants, in linear transformation of theta functions 555 559 Constants, invariant in rational transformation 9 88 144 148 150 Contact curves see Curves and Convergence of an automorphic series 350 Convergence of transformed theta function 538 Coresidual sets of places on a Riemann surface 135 ff. 213 Coresidual sets of places on a Riemann surface, are equivalent sets 136 Coresidual sets of places on a Riemann surface, enter in statement of Abel’s theorem 210 Correspondence of Riemann surfaces 3 ff. 81 639 642 647 648 649 654 662 Covariant see Invariant. Cubic surface associated with a plane quartic curve 382 389 Curves, Abel’s theorem for 281 Curves, adjoint curves 121 129 Curves, as alternative interpretation of fundamental algebraic equation 11 Curves, bitangents of a plane quartic curve 384 Curves, Cayley’s theorem for 141 Curves, contact curves 381 Curves, coresidual and equivalent sets upon 134 136 Curves, correspondence of see Correspondence; Curves, curves in space 157 ff. 166 664 Curves, general form of Pl 124 Curves, generalisation 40 Curves, inflexions and bitangents in connection with theory of correspondence 644 646 Curves, inflexions of a plane quartic in connection with the gap theorem 36 Curves, special sets upon 146 ff. Curves, transformation of see Birational Invariants and Curves, Weierstrass’s canonical equation for 93 103 Cusps 11 114 Darboux 666 De Jonquieres 137 Dedekind 57 Deficiency of a Riemann surface 7 55 60 Defining relation for theta functions 443 Definition equation of theta functions of general order 448 Degenerate Abelian integrals 657 Dependence of the poles of a rational function 27 Dersch 647 Differential equations of inversion problem 225 ff. Differential of theta functions see Addenda Differentials of integrals of first kind 25 62 67 127 169 Dimension of an integral function 48 ff. 55 Dimension, condition of dimensions 49 Dini 239 Dirichlet 246 600 Discriminant of a fundamental set of integral functions 74 101 124 Dissection of the Riemann surface 26 529 253 257 569 297 550 560 Double points of a Riemann surface (or curve) 1 2 3 11 114 Double tangents of a plane curve 644 646 Eisenstein 246 674 Elementary integrals see Integrals. Epstein 342 Equivalence, meanings of sign of 236 256 261 264 487 Equivalent sets of places on a Riemann surface 134 ff. 136 213 Essential factor of the discriminant 60 74 124 Euler 159 Existence references 14 Existence theorems, algebraically deducible 78 Expression of any rational function 77 176 212 Expression of fundamental integral functions 105 ff. Expression of half-integer characteristic by means of a fundamental system 301 487 500 502 Factorial functions 392 ff. Factorial functions, connection with automorphic functions 439 ff. Factorial functions, definition of 396 Factorial functions, expressed by factorial integrals 403 Factorial functions, expressed by fundamental factorial function 413 Factorial functions, used to express theta functions 423 426 Factorial functions, which are everywhere finite 399 Factorial functions, with fewest poles 406 Factorial integrals 898 Factorial integrals, expression of factorial function by means of that Factorial integrals, integral 412 Factorial integrals, fundamental, having only poles 408 Factorial integrals, simplified form of that integral 411 Factorial integrals, which are everywhere finite 399 Fagnano 638 Forsyth 2 3 7 9 10 13 14 15 16 21 24 25 29 39 90 114 122 123 144 150 198 212 233 296 327 373 395 421 439 441 442 445 459 531 577 578 Frahm 383 Fricke 639 648 Frobenius 342 387 447 474 486 491 500 516 517 521 522 525 586 588 589 598 628 629 630 632 633 666 668 674 676 Frost 389 Fuchs 206 566 Function, 292 324 338 516 Function, 287 292 320 Function, automorphic 352 ff. 439 ff. Function, factorial see Factorial; Function, integral see Rational and Function, prime 172 205 360 363 428 Function, radical 374 390 565 Function, rational see Rational; Function, theta see Theta functions and Fundamental algebraical equation 10 113 Fundamental rational function, Weierstrass’s 171 175 177 178 ff. 182 Fundamental set for the expression of rational integral functions 48 ff. 55 56 57 105 ff. Fundamental system of theta characteristics 301 487 500 502 G 338 340 465 468 G see Characteristics. G 174 189 200 Gap theorem 32 34 93 174 Gasorati 579 Gauss 559 600 674 Geiser 383 Geometrical investigations 113 see Curves. Gopel 246 338 339 Gordan 131 142 168 183 241 244 255 288 295 892 423 448 544 545 556 578 623 Goursat 663 Grade, of a polynomial 120 Grassman 137 Greenhill 639 Group, Gopel see Characteristics. Halphen 124 165 364 370 421 473 474 639 665 Hamburger 2 Hancock 296 326 Harkness 2 10 14 15 16 21 24 25 79 101 124 239 342 Harnack 222 Hensel 57 64 78 118 Hensel’s determination of fundamental integral functions 105 ff. hermite 238 246 448 452 538 577 600 615 632 689 663 666 674 Hettner 177 654 hilbert 665 Homogeneous variables 118 441 Homographic behaviour of differentials of integrals of first kind 26 Humbert 222 255 340 486 Hurwitz 41 392 689 648 651 653 654 Hyperelliptie surfaces 80 ff. 152 158 373 Independence of the 446 447 Independence of the poles of a rational function 27 Index at the infinite place of Weierstrass’s canonical surface 129 Index of a place on a Riemann surface 122 123 124 Infinitesimal on a Riemann surface 1 2 3 Infinitesimal periods 238 573 Infinities of rational function 27 ff. Infinity, the places at infinity on a Riemann surface, algebraic treatment of 118 Inflexions of a plane curve 36 40 646 Integral functions see Rational and Transcendental. Integrals, algebraic expression of 65 ff. 127 131 163 185 189 194 Integrals, all derivable from integral of third kind 22 Integrals, degenerate 657 Integrals, factorial see Factorial ; Integrals, formulae connecting with logarithmic differential coeffcients of theta functions 289 290 320 Integrals, hyperelliptie 195 Integrals, Riemann’s, normal elementary 15 Interchange of argument and parameter 16 185 187 189 191 194 206 Interchange of period loops see Transformation. Invariants in birational transformation, for transformation of the Invariants in birational transformation, dependent variable 74 124 Invariants in birational transformation, the 9 144 148 150 Invariants in birational transformation, the 38 653 Invariants in birational transformation, the contact 281 427 Invariants in birational transformation, the number 7 Invariants in birational transformation, the ratios of 26 153 Inversion theorem, by radical functions 390 Inversion theorem, in the hyperelliptic ease 317 324 Inversion theorem, Jacobi’s 285 ff. 270 Inversion theorem, solution of 239 242 244 275 J 221 jacobi 165 206 221 230 235 237 246 360 577 600 639 657 Jacobian functions, their expression by theta functions 588 594 Jacobian functions, their periods, are generalisation of theta functions 579 588 Jacobian functions, there exists a homogeneous polynomial relation connecting any 594 Jacobi’s inversion theorem see Inversion. JORDAN 248 392 549 623 639 666 669 Joubert 639 K 837 342 448 459 477 529 600 607 615 628 658 661 663 Kiepert 688 639 Klein 9 25 156 159 169 177 342 343 360 373 378 383 392 429 430 431 436 438 439 544 639 648 658 654 Klein, prime form 360 427 430 433 Kohn 387 Kowalevski 658 659 662 663 Krause 296 342 468 486 600 623 674 Krazer 477 486 555 600 627 kronecker 56 79 124 445 577 600 629 631 639 666 669 Kummer 340 Lagrange 280 Laguerre 632 666 Laurent’s theorem, for 444 Left side of period loop 529 Liiroth 239 Lindemann 153 156 222 647 Linear transformation see Transformation. Linearly independent 154 Linearly independent columns of periods 575 Linearly independent Jacobian functions 594 Linearly independent theta functions 446 447 Loops, period loops on a Riemann surface 21 529 Lots, of sets of places on an algebraic curve, or Riemann surface 135 Malet 663 Mathews 165 Matrices 248 283 580 666 669 Minding 221 Mittag — Leffler’s theorem for uniform function on a Riemann surface 202 Mittag — Lejler 202 Moduli of periodicity see Periods. Moduli, for the hyperelliptie equation 88 Moduli, of the algebraic equation, are 9 144 148 150 Morley 2 10 14 15 16 21 24 25 79 101 124 239 342 Multiplication, by an integer, for theta functions 527 Multiplication, complex, of theta functions 629 ff. Multiply-periodic 236 see Inversion. Netto 20 90 Neumann 14 17 169 296 531 Noether 12 29 32 124 131 134 137 142 145 149 156 165 168 180 272 292 295 390 392 430 486 522 544 566 654 665 Noether’s (Kraus’s) 156 157 Normal equation for a Riemann surface 83 91 103 143 145 152 Normal integrals (Riemann’s) see Integrals. Number of independent products of 154 Number of Jacobian functions 594 Number of odd and even theta functions 251 Number of theta functions of general order 452 463 Order of a theta function 448 Order of small quantity on a Riemann surface 2 Parameter, interchange of argument and parameter see Interchange. Parameters, in the algebraic equation see Constants. Period characteristics see Characteristics. Period loop see Loops.
Реклама
 |
|
О проекте
|
|
О проекте



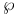 Function
Function  -polynomials
-polynomials 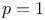 , or
, or 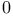
 pel groups and systems of
pel groups and systems of 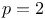 ,
, 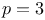
 cker’s equations for
cker’s equations for  function
function  theta functions with half-integer characteristics
theta functions with half-integer characteristics moduli
moduli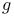 -places
-places 
 Jacobian functions of same periods and parameter
Jacobian functions of same periods and parameter 
 in number
in number