Авторизация
Поиск по указателям
Baker H.F. — Abel's Theorem and the Allied Theory Including The Theory of the Theta Functions
Обсудите книгу на научном форуме Нашли опечатку?
Название: Abel's Theorem and the Allied Theory Including The Theory of the Theta FunctionsАвтор: Baker H.F. Аннотация: Classical algebraic geometry, inseparably connected with the names of Abel, Riemann, Weierstrass, Poincaré, Clebsch, Jacobi and other outstanding mathematicians of the last century, was mainly an analytical theory. In our century the methods and ideas of topology, commutative algebra and Grothendieck's schemes enriched it and seemed to have replaced once and forever the somewhat naive language of classical algebraic geometry. This classic book, written in 1897, covers the whole of algebraic geometry and associated theories. Baker discusses the subject in terms of transcendental functions, and theta functions in particular. Many of the ideas put forward are of continuing relevance today, and some of the most exciting ideas from theoretical physics draw on work presented here.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1897Количество страниц: 684Добавлена в каталог: 25.03.2006Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Periodicity of a (1,1) correspondence 650 Periods of Riemann’s integrals 16 21 Periods of Riemann’s integrals, for integrals of second kind 323 Periods of Riemann’s integrals, general theory of systems of periods ff. 579 ff. Periods of Riemann’s integrals, general transformation 536 538 Periods of Riemann’s integrals, linear transformation of periods 532 Periods of Riemann’s integrals, of degenerate integrals 657 Periods of Riemann’s integrals, of factorial integrals 404 Periods of Riemann’s integrals, Riemann’s and Weierstrass’s relations for the periods of integrals of the first kind, and of associated integrals of the second kind 197 285 581 587 Periods of Riemann’s integrals, rule for half-periods on a hyperelliptie surface 297 Picard 14 165 594 659 Picard’s theorem (Weierstrass’s) 658 Pick 360 430 639 Pl 124 165 Pl 166 Pl 123 124 Places, after linear transformation 562 Places, branch places 7 9 46 74 122 297 569 Places, determination of, for a Riemann surface with assigned period Places, loops 567 Places, for a hyperelliptie surface 297 563 Places, of a Riemann surface 1 2 3 Places, the places 255 Places, their geometrical interpretation 265 266 Places, where a rational fnnetion is infinite, to order less than 38 41 90 653 Poincar 239 372 373 439 486 594 654 659 663 Poles see Inflnities. Polynomial, 141 Polynomial, adjoint 121 128 Polynomial, algebraic treatment of 120 Polynomial, expression of rational functions, and algebraic integrals by means of adjoint polynomials 156 see Curves. Polynomial, grade of 120 Polynomial, transformation of fundamental equation by 142 154 Positive direction of period loop 529 Primary and associated systems of factorial fnnctions 397 Prime function (or form) see Function. Pringsheim 445 Product expression of uniform transcendental function with single essential singularity 205 Prym 2 296 342 392 477 486 511 566 600 627 Quartic. Double tangents of plane quartic curve 381 390 647 Quotients of theta functions 310 311 390 516 Radical function see Function. Rational function, of order 1, algebraic expression of, by adjoint polynomials 125 ff. 156 Rational function, of order 1, expressed by Riemann’s integrals 24 212 Rational function, of order 1, expressed by Weier- strase’s function 176 Rational function, of order 1, fundamental integral rational functions, algebraic determination of 105 ff. Rational function, of order 1, infinities of, Riemann- Roch theorem, Weierstrass’s gap theorem 27 ff. Rational function, of order 1, integral function 47 ff. 55 91 ff. Rational function, of order 1, is an uniform function on the Riemann surface whose only infinities are poles 27 Rational function, of order 1, of order 38 137 Rational function, of order 1, of the second order 80 ff. Rational function, of order 1, only exists when 8 Rational function, of order 1, special 25 137 Rational function, of order 1, Weierstrass’s fundamental 171 175 177 ff. 182 Reciprocal sets of zeros of adjoint polynomials 134 Residual sets of places 135 Residue, fundamental residue theorem 232 189 20 Reversible transformation see Birational. Richelot 221 230 529 600 668 Riemann 1 2 6 9 13 45 47 77 113 115 246 248 255 296 343 397 409 628 Riemann and Weierstrass’s period relations 197 285 581 587 Riemann — Roch theorem 44 133 Riemann — Roch theorem, for factorial functions 405 Right side of period loop 529 Ritter 360 373 392 429 439 442 Roch 29 Rosanes 666 Rosenhain 221 222 246 311 459 600 607 662 Row and column see Matrices Salmon 5 6 7 11 39 117 124 136 144 165 267 383 389 Schepp 239 Schl 666 Schottky 32 101 283 296 340 343 345 360 371 372 373 387 448 461 469 544 628 Schottky — Klein prime form and function 360 430 433 Schubert 665 Schwarz 14 654 Scott 473 Sequence, theorem of 114 161 165 Sequent sets of places 135 Sets of places on a Riemann surface or algebraic curve 135 see Special. Sign of equivalence and congruence 236 256 261 264 487 smith 12 600 639 666 674 675 Sohnke 689 Special correspondences on a Riemann surface 648 Special rational functions 25 62 137 Special sets of zeros of adjoint polynomials 134 147 Special transformation of a theta function ff. 639 660 Stahl 288 301 392 430 486 502 Stickelberger 666 Stolz 2 Strength of assigned zeros, as determinators of a polynomial 133 Supplementary transformations of a theta function 552 Sylvester 136 System, G see Characteristics. Syzygetic characteristics 487 542 Taber 668 Tables of Characteristics 303 305 Tangents, double, of a plane curve, by the principle of correspondence 644 646 Theta functions, addition theorem for hyperelliptic 882 337 Theta functions, algebraic expression for hyperelliptic 435 Theta functions, algebraic expression of first logarithmic derivatives of 288 290 320 Theta functions, algebraic expression of quotients of 310 311 390 426 Theta functions, algebraic expression of second logarithmic derivatives of 293 324 329 333 Theta functions, convergence of 247 Theta functions, determination of, from periodicity 444 Theta functions, General theta function of first order 283 444 Theta functions, General theta function of first order, addition theorems for 457 472 481 513 521 Theta functions, General theta function of first order, expression of Jacobian functions by means of 594 Theta functions, General theta function of first order, G see G Theta functions, General theta function of first order, period relations 285 197 581 587 Theta functions, General theta function of first order, second logarithmic derivatives of 516 Theta functions, hyperelliptic 296 ff. Theta functions, identical vanishing of 258 271 276 303 Theta functions, number of odd and even 446 Theta functions, period properties of 249 Theta functions, Riemann’s functions not the most general 248 628 Theta functions, Riemann’s theta functions 246 ff. Theta functions, solution of inversion problem by means of 275 324 390 426 ff. Theta functions, Theta functions of second and higher order 448 Theta functions, Theta functions of second and higher order, every 453 Theta functions, Theta functions of second and higher order, expression of, number of linearly independent 452 463 Theta functions, Theta functions of second and higher order, of order 2, of special kind 509 510 Theta functions, Transformation of theta functions see Transformation; Theta functions, Transformation of theta functions, characteristics of theta functions see Characteristics; Theta functions, Transformation of theta functions, complex multiplication of theta functions 629 ff. 639 660 Theta functions, Transformation of theta functions, hyperelliptic case 433 Theta functions, Transformation of theta functions, particnlar cases 430 ff. Theta functions, Transformation of theta functions, theta functions Theta functions, Transformation of theta functions, expressed by factorial functions and simpler theta fnnetions 426 Theta functions, zeros of 252 255 258 567 Thomae 288 296 318 533 556 600 Thompson 436 toeplitz 383 Transcendental uniform function 200 Transcendental uniform function, application of Laurent’s theorem when the function is integral 444 Transcendental uniform function, expressed in prime factors 205 Transcendental uniform function, Mittag- Leffler’s theorem for 202 Transformation of characteristics see Characteristics. Transformation of periods 528 534 539 551 553 555 559 568 Transformation of the algebraic equation (or Riemann surface) 3 143 145 151 152 654 655 Transformation of theta functions 535 Transformation of theta functions for any odd order, general theorem 614 Transformation of theta functions for hyperelliptic case 568 Transformation of theta functions of second order 603 617 Transformation of theta functions, composition of 551 Transformation of theta functions, for any odd order, constants in 620 622 Transformation of theta functions, linear transformation 539 Transformation of theta functions, linear transformation constants in 554 559 Transformation of theta functions, special transformations 629 660 Transformation of theta functions, supplementary transformations 552 Transformation of theta functions, when coefficients not integers 625 uniform see Rational and Valentin 101 Valentiner 124 165 665 Vanishing of theta function 253 258 271 276 303 Variables, homogeneous 118 429 441 Voss 137 Weber 8 56 270 272 37 387 392 430 460 486 538 538 559 600 615 620 639 674 Weierstrass 32 93 99 101 177 195 197 205 231 239 242 246 301 311 317 326 389 443 474 486 525 570 571 572 573 577 579 594 628 653 654 658 666 Weierstrass’s gap theorem 32 34 93 174 Weierstrass’s gap theorem, canonical surface (or equation) 90 ff. 93 Weierstrass’s gap theorem, fundamental rational fnnction 171 175 177 178 182 189 Weierstrass’s gap theorem, period relations 197 ff. 285 581 587 Weierstrass’s gap theorem, rule for characteristics of hyperelliptic theta functions 569 Weierstrass’s gap theorem, special places which are the poles of rational functions of order less than 34 ff. Weierstrass’s gap theorem, theorem for degenerate integrals 658 White 165 Wiltheiss 842 600 629 660 662 674 Wirtinger 340 486 578 628 Zeros, generalised zeros of a polynomial 121 Zeros, zeros of Riemann theta function 252 Zeta function 287 292 320 Zeuthen 647
Реклама
 |
|
О проекте
|
|
О проекте



 cker
cker  , ...,
, ..., 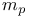
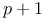

 -polynomials
-polynomials 
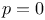
 fli
fli  pel
pel 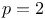
 theta functions of same order, periods, and characteristic, connected by a homogeneous polynomial relation
theta functions of same order, periods, and characteristic, connected by a homogeneous polynomial relation