|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| McShane E.J., Botts T.A. — Real Analysis |
|
|
 |
| Предметный указатель |
Lebesgue, H., differentiability of 184
Lebesgue, H., Lebesgue decomposition 178
Lebesgue, H., Lebesgue dominated convergence theorem 140
Lebesgue, H., Lebesgue integral 1261
Lebesgue, H., Lebesgue ladder 161
Lebesgue, H., Lebesgue summable function 133
Left derivative 111
Left limit 39 58
Length of graph of function 75
Limit, double 80
Limit, iterated 80 81
limit, left 39 68
Limit, lower 54
Limit, operations with 35
limit, right 38 58
Limit, upper 54
Line segment 72
Linear bounded 210
Linear function 90
Linear functional 209ff 216ff
Linear operator 209
Linear positive 216
Linear space 202
Linear subspace 202
Lipschitz, R., Lipschitz condition 77 78 80 97 103 112 113 210
Lower bound 20 28
Lower Darboux — Stielijes integral 168
Lower derivate 110
Lower integral 133
Lower limit 54
Lower semicontinuous function 74
Lusin, N. N., Lusin’s theorem 159
Matrix 121
Matrix, diagonal 241
Matrix, hermitian 241
Maximal dement 28
Maximality principle 29ff 251ff
Maximum, attained 71 76
Maximum, relative 117
Mean value theorem 117 121
Mean value theorem, first (for integrals) 151
Mean value theorem, second (for integrals) 192
Measurable function 146ff 161
Measurable set 153ff
Measure 153ff 173ff
Measure, finite 143
Measure, signed 175
Measure, zero 138 145
Mesh, of partition 165
Metric 59 204
Metric, density 188
Metric, space 59ff
Minimum, attained 71 76
Minimum, relative 116 121
Minkowski, H., Minkowski inequality 59 164
Module 202
Modulus of continuity 78
Monomial function 72
Monotone Convergence Theorem 137
Monotone function 58 98ff
Moore, E. H. 82
Natural numbers 4
Negative variation 100 106
Neighborhood, and open sets 44ff
Neighborhood, basic 32 39
Neighborhood, deleted basic 32
Neighborhood, deleted relative 68
Neighborhood, general 44
Neighborhood, Spherical 60
Neutral dement 9
Nikodym, O, Radon — Nikodym theorem 180ff
Nonmeasurable set 157
Nonordered sum 34
Nonoverlapping intervals 108
Norm 204ff
Norm, convergence in 225
Norm, supremum-absolute 204
Norm, uniform 204
Normal space 95 97
Normed linear space 204
Nowhere-differentiable function 113ff
Numbers, cardinal 5
Numbers, complex 161
Numbers, extended real 26
Numbers, natural 4
Numbers, real 24ff
Oldened  -tuple 5 -tuple 5
Oldened field 14
Oldened pair 2
One-point compactificaiion 80
One-to-one correspondence 4
One-to-one function 4
Open covering 50
Open interval 27
Open set 44ff
Operator, Hermitian (symmetric, self-adjoint) 223 241ff
Operator, linear 209
Order 14 253
Order, convergence 54
Order, partial 27
Ordering 253
Orthogonal complement 224
Orthogonal projection 223
Orthogonal vectors 221
Orthonormal set 227 232
Parseval, M. A., Parseval’s equation 229 232
Partial derivatives 118 125
Partial order 27ff
Partially ordered set 28
Partition 106 165
Peano, O., Peano postulates 6
Permutation 5 122
Perpendicular 221
Plancherel, M., Fourier — Plancherel transform 238
Polynomial function 72
Positive linear functional 216
Positive variation 100 106
PRODUCT 13
Product, cartesian 43
Product, inner 219
Product, topological 42
Projection, orthogonal 223 229
Quadratic functional 224ff
Radon — Nikodym theorem 180ff
Radon, J., Radon — Stieltjes integral 133
Range (of a function) 3
Rational numbers 18
Rational subfield 16
Real number system 24
refinement 40
Reflexive relation 40
Regular convergence 183
Regular topological space 84
Regularity (for measurable sets) 157
Relation 4
Relation, antisymmetric 27
Relation, refinement (among topologies) 40
Relation, reflexive 40
Relation, transitive 40
Relative neighborhoods 68
| Relative topologies 49ff
Representation of linear functionals 211
Representation of step function 126
Resolution of the identity (spectral resolutions) 247
Restriction of a function 3
Riemann, B., Riemann and Riemann — Stieltjes integral 165ff
Riemann, B., Riemann sum 165
Riemann, B., Riemann — Lobesgue theorem 151 231
Riesz, F., Riesa — Ficher theorem 228 232
Riesz, F., Riesz representation theorem 216ff
Right derivative 111
Right limit 38 58
Ring, of sets 173
Rolle’s Theorem 117
Saks, S 159
scalar 202
Schwarz, H. A., Cauchy — Buniakowski — Schwarz inequality 59 162
Segment 72
Self-adjoint operator 223
Semicontinuily 73ff
Semicontinuous function 74
Separable 47
SEQUENCE 33
Sequence, convergent 34
Sequence, sum of 33
Series 34
Series, absolutely convergent 136
Series, convergent 34 37
Series, unconditionally convergent 34
Set 1ff
Set, arcwise connected 72
Set, Borel 164
Set, cardinal number of a 5
Set, closed 46ff
Set, compact, SOS Set, convex 222
Set, countable 5
Set, countably infinite 5
Set, dense 21 47
Set, measurable 153ff
Set, open 44ff
Set, orthonormal 227
Set, ring of 173
Set, separable 47 208
Set, star-shaped 72
Set, well-ordered 6 252
Signed measure 175
Simple function 212
Singular function of sets 178
Space,  202ff 202ff
Space, 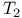 40 40
Space, Banach 204
Space, function 202ff
Space, Hausdorff 40
Space, Hilbert 219ff
Space, linear 202
Space, metric 59ff
Space, normal 95 97
Space, normed linear 204
Space, product 42ff
Space, regular 84
Space, spanned by a set 22
Space, subspace 202
Space, topological 39ff
Spectral resolution 247
Spherical neighborhood 60
Star-shaped set 72
Stieltjes, T. J., Lebesgue — Stieltjes integral 133
Stieltjes, T. J., Lebesgue — Stieltjes integration 126ff
Stieltjes, T. J., Riemann — Stieltjes integral 165ff
STONE, M. H.., Stone — Weierstrass theorem 87ff
Strictly isotone or antitone function 98
Strong convergence 225
Subdirected function 37 38
Subdirection 37
Subfield 10 11
Subfield, rational 16
Subsequence 38
Substitution, in multiple integrals 196ff
Substitution, in simple integrals 193ff
Sum, nonordered 34
Sum, of a series 34
Sum, of elements of a field 13
Summable function 133ff 161
Supremum 20 28
Supremum, essential 203
Symmetric operator 223
Taylor’s Formula 116ff
Tietze, Tietze’s extension theorem 96 97
Topological space 39ff
Topological space, convergence in 40ff
Topological space, functions on a 68ff
Topological space, normal 95 97
Topological space, product 42 52
Topological space, regular 84
topology 39
Topology, equivalent 40 41
Topology, of 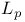 spaces 206ff spaces 206ff
Topology, relative 49ff
Total variation 100 106
Transfinite inductive, definition 254
Transfinite inductive, proof 253
Transitive relation 27 40
Tukey, J. W. 30
Tychonoff, A., Tychopoff’s theorem 52 260
U-function 126ff
Ultimately 33 35
Unconditionally convergent series 34
Uniform continuity 77 78 97
Uniform convergence 82 84ff 93 102 225
Uniform norm 204
Uniformly continuous function 78
union 2
Uniqueness of limit in Hausdorff space 41
Uniqueness, for Fourier expansion 233
Uniqueness, for Fourier transform 240
Uniqueness, of complete ordered fields 22ff
Upper and lower Darboux — Stieltjes integrals 168
Upper bound 20 28
Upper Darboux — Stieltjes integral 168
Upper derivate 110
Upper integral 133
Upper limit 54
Upper semicontinuous function 74
Upwardly directed set 28 128
Urysohn, P., Urysohn’s lemma 97
Value, absolute 15
Variation, positive 100 106
Variation, total 100 106
Variations, bounded 99ff 103 106
Variations, negative 100 106
Vector space 202
Vectors 50 202
Vectors, orthogonal 221
Volume 108 126
Weak convergence 225
Weierstrass, K., Bolzano — Weierstrass theorem 53
Weierstrass, K., Stone — Weierstrass theorem 87ff
Well-ordered set 6 252
Welt-ordering theorem 253
Zermelo, E. 29 253
Zorn, M., Zorn’s lemma 251
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -tuple
-tuple 
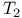
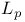 spaces
spaces