|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ford L. Ч Automorphic Functions |
|
|
 |
| ѕредметный указатель |
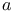 -cuts 229 233 266 -cuts 229 233 266
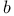 -cuts 229 233 266 -cuts 229 233 266
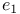 , , 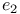 , , 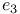 150 157Ч162 150 157Ч162
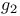 , , 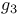 149 151Ч157 160 149 151Ч157 160
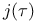 151Ч157 159 160 163 308 151Ч157 159 160 163 308
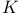 see Multiplier see Multiplier
 see Genus see Genus
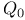 30 30
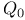 , a group allied to 35 78 79 , a group allied to 35 78 79
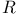 , the region, defined 44; see Fundamental region , the region, defined 44; see Fundamental region
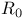 see Fundamental region see Fundamental region
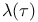 157Ч163 308 157Ч163 308
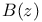 83 86 88 144Ч146 148Ч150 158Ч162 307 83 86 88 144Ч146 148Ч150 158Ч162 307
Abramowicz, C. 323
Accessible boundary points 189Ч 195 197 199
Alezais, R. 316
Algebraic functions 221 225 229Ч 249 252 266 278 308
Algebraic functions, of genus greater than zero 233Ч244 247Ч249 252 266 278
Algebraic functions, of genus one 239 240 278
Algebraic functions, of genus zero 229Ч233 245Ч247 252
Algebraic relations between automorphic functions 94Ч98 149 160 163 231
Analytic curve 201
Angles at vertices of ordinary cycle 62 89 93 112 130
Anharmonic ratio see Cross ratio
Anharmonic ratios, group of 34 49 78 159
Area of 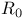 75 75
Area of 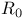 , theorems 167Ч169 , theorems 167Ч169
Automorphic function, definition of 83
Automorphic functions, simple 86Ч88
Automorphic functions, simple, algebraic relations 94Ч98
Automorphic functions, simple, and differential equations 98Ч101
Automorphic functions, simple, behavior at vertices and parabolic points 88Ч91
Automorphic functions, simple, for finite group 102 131 136
Automorphic functions, simple, for modular group 155
Automorphic functions, simple, for modular sub-group 162
Automorphic functions, simple, for periodic and allied groups 144Ч146
Automorphic functions, simple, poles and zeros 91Ч94
Automorphic functions, simple, uniformization by means of 233Ч247 266Ч279
Axel, H. 322
Bagnera, G. 31 52
Baker, H. F. 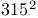
Bianchi, L. 313 314 319
Bieberbach, L. 148 167 172 318 321 322 323
Biermann, O. 312 313
Birkhoff, G. D. 322
Blumenthal, O. 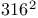 317 317
Boundary, behavior of mapping function on 187Ч203
Boundary, circular arc 202
Boundary, continuation of mapping function across 201Ч203
Boundary, elements 195Ч198
Boundary, of R 47Ч49
Branch points 165 181 213 226 227 229 249 250 290 309
Brod n, T. 317 n, T. 317
Brouwer, L. E. J. 31 93
Burckhardt, H. 314
Burnside, W. 106 313
Cahen, E. 320
Carath odory, C. 165 195 odory, C. 165 195
Caspar, M. 318
Cassel, G. 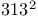 314 314
Chain of points 176 179
Chazy, J. 319
circle 8Ч15 (see also Inversion Conformal Fixed Isometric Unit Etc)
Circular arc boundaries 202
Circular arc boundaries, triangle 305
Combination, method of 56Ч59 279
Combined regions, mapping of 203Ч205
Concentric slits 265 266
Conformal mapping 164Ч219
Conformal mapping of multiply connected region of planar character on region bounded by complete circles 279Ч283
Conformal mapping of neighborhood of parabolic point 90
Conformal mapping of neighborhood of regular singular point 298
Conformal mapping of plane on plane 3
Conformal mapping of plane on plane region 2
Conformal mapping of plane simply connected region on circle 179Ч187
Conformal mapping of region and subregion 166
Conformal mapping of region bounded by complete circles on second such region 282
Conformal mapping of semicircle on circle 188
Conformal mapping of simply connected finite-sheeted Conformal mapping regions 213Ч216
Conformal mapping of surface of genus zero on plane 229
Conformal mapping of two-sheeted circular region on circle 181
Conformal mapping, and groups of linear transformations 216Ч219
Conformal mapping, by 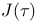 157 157
Conformal mapping, of circle on circle 32
Conformal mapping, of circle on plane finite region 169Ч175
Conformal mapping, of combined regions 203Ч205
Conformal mapping, of finite plane on finite plane 3
Conformal mapping, of half plane on circular arc triangle 305
Conformal mapping, of limit regions 205Ч213
Conformal mapping, of multiply connected region of planar character on slit region 262Ч265
Congruent configurations 37
Conjugate imaginary 8
Connectivity of algebraic surfaces 225Ч229
Connectivity of regions 221Ч229
Constant automorphic function 94
Continuation of mapping function across the boundary 201Ч203
Convergence in mapping limit region 207Ч 211
Convergence of iterative process 183 184
Convergence of series and products connected with the group 115 116
Convergence of series for 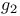 151 152 151 152
Convergence of subsequence of a set of functions 267Ч271
Convergence of subsequence of mapping functions 271Ч273
Convergence of theta series 104Ч108
Cosine 85 144 220 233 307
Cotangent, series for 154
Courant, R. 148 319
Craig, C. F. 318
Cross (anharmonic) ratio 4 7 34 49 78 159
Cross-cut 222
cube 124Ч127 136Ч138
Curves defining boundary element 196Ч198
Cycles, ordinary 59Ч62 72 73 89 130
Cycles, parabolic 62Ч64 72
Cyclic groups 51Ч56 66 Parabolic Hyperbolic and
Dalaker, H. H. 323
de Brun, F. 313
Deformation of lengths by inversion in sphere 118
Deformation of lengths by linear transformation 24 25
Deformation theorem, for circle 171Ч175
Deformation theorem, general 175Ч177 274
Del Pezzo, P. 314
Delta$ 150 151 155
Derivative of automorphic function 98 104 131
Derivative of automorphic function, Schwarzian 98 291 302
Determinant of linear transformation 2
Diameter of curve 198
Differential equations 98Ч101 284Ч309
Differential equations, connection with groups 284Ч286
Differential equations, hypergeometric equation 303Ч308
Differential equations, quotient of two solutions 287Ч293 296Ч298
Differential equations, regular singular points 293Ч298
Differential equations, triangle functions 305Ч308
Differential equations, with algebraic coefficients 308 309
Differential equations, with rational coefficients 299Ч308
Differential equations, with three singular points 303Ч308
Differential equations, with two singular points 303
Dihedral group 129
Discontinuous groups 35
Discrete set of points 277
Dixon, A. C. 315
Domain of existence of function 83
Doubly periodic functions see Elliptic functions
Doubly periodic groups 35 38 139Ч146 148Ч151 238 243
Dyck, W. 312
DТOvidio, E. 314
Edge separating square elements 251
Element, square 213 250
Elementary groups 66 117Ч147
Elementary groups, allied to periodic 140Ч143
Elementary groups, determination of all finite 129Ч136
| Elementary groups, finite 117Ч138
Elementary groups, of regular solids 123Ч129
Elementary groups, simply and doubly periodic 139 140
Elementary groups, with one limit point 139Ч146
Elementary groups, with two limit points 146 147
Elliptic cyclic groups 55 109 129 133 217
Elliptic functions 83 144Ч146 148Ч150 158 159 238 240 247 307 309
Elliptic modular functions 148Ч163
Elliptic modular functions, 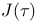 151Ч157 151Ч157
Elliptic modular functions, 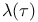 157Ч159 160Ч162 157Ч159 160Ч162
Elliptic modular functions, algebraic relations 159 160 163
Elliptic modular functions, definition 148
Elliptic surface 227 257
Elliptic transformations 19 20 23 28 88 121 288 298
Emch, A. 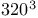
Equation, indicial 294 298
Equations, differential see Differential equations
EulerТs formula 128 228 246
Existence, domain of 83
Exponents at regular singular point 294 298Ч301 303
Extended groups 136Ч138
Falckenberg, H. 321
Families, normal 268
Fatou, P. 317
Finite groups 34 37 38 49 55 66 78 102 117Ч138 245 246 303 308
Finite groups, determination of all finite groups 129Ч136
Finite groups, fixed points of 132 133
Finite groups, of regular solids 123Ч129
Finite-sheeted simply connected regions 213Ч216
Fixed circles of linear transformation 19Ч22 28Ч32 66 67
Fixed points at infinity 75Ч82 105 139Ч147
Fixed points of linear transformation 6Ч8 24 67 88 109 130Ч135 141
Ford, L. R. 320
Forsyth, A. R. 314 321
Four group 129 133
Fricke, R. 148 319 320 323
Fubini, G. 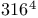 322 322
Fuchs, L. 31 12 317
Fuchsian functions 87
Fuchsian functions, and differential equations 302 303 306 309
Fuchsian functions, uniformization by means of 240 241Ч244 247 simple Elliptic
Fuchsian groups 66 67Ч82
Fuchsian groups, cycles 72 73
Fuchsian groups, fixed points at infinity 75Ч82
Fuchsian groups, fundamental region 69Ч71 73Ч75 77
Fuchsian groups, generating transformations 71 72
Fuchsian groups, limit points 67Ч69
Fuchsian groups, of first and second kinds 73Ч75
Fuchsian groups, of the first kind 68 73Ч75 108 237 308
Fuchsian groups, of the second kind 68 73Ч75 106Ч109 116 258
Fuchsian groups, the transformations 67
Fueter, R. 321 323
Fuhr, H. 322
Function see Algebraic Automorphic Elliptic Elliptic Periodic Polyhedral Rational Triangle Etc. function
Function, groups 64Ч66 86 109
Fundamental region of a group 37Ч39 65 75 77 92 94 237 240 243
Fundamental region of a group, boundary of 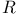 47 48 47 48
Fundamental region of a group, definition of region 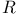 44 44
Fundamental region of a group, genus of 238
Fundamental region of a group, region 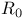 69 69
Fundamental region of a group, regions congruent to 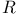 44Ч46 44Ч46
Fundamental region of a group, the cycles 59Ч64
Fundamental region of a group, the sides 47
Fundamental region of a group, the vertices 38 48 49 54 55 58 61 73 74 78 80 82 136 142 143 148 153 161 217 238 248 258 274 278 307
Garnier, R. 318 319
Generating transformations 34 39 50 51 65 71 72
Generating transformations, relations between 62
Genus, definition 227
Genus, of algebraic function 227
Genus, of fundamental region 238 (see also Algebraic functions)
Geometric interpretation of linear transformation 13 14 26Ч28
Giraud, G. 320
Gordan, P. 315
Got, Th 322
Group of differential equation 286
Groups of linear transformations 33Ч66
Groups of linear transformations, cycles 59Ч64
Groups of linear transformations, cyclic groups 51Ч56
Groups of linear transformations, function groups 64Ч66
Groups of linear transformations, fundamental region 37Ч39
Groups of linear transformations, generating transformations 50 51
Groups of linear transformations, isometric circles 39Ч41
Groups of linear transformations, limit points 41Ч44
Groups of linear transformations, properly discontinuous 35 36
Groups of linear transformations, region 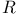 44Ч50 44Ч50
Groups of linear transformations, the method of combination 56Ч59
Groups of linear transformations, transforming a group 36 37 Kleinian Schottky Etc. groups)
Hecke, E. 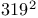
Herglotz, L. 317
Hilb, E. 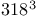 319 321 319 321
Hilbert, D. 316 319
Homographic transformation 1
Humbert, G. 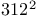 321 321
Hurwitz, A. 148 185 311 313 317
HurwitzТ theorem 185
Hutchinson, J. I. 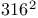
Hyperbolic cyclic groups 52Ч54 147
Hyperbolic function 83
Hyperbolic transformations 18 19 23 28
Hyperelliptic functions 247Ч249
Hyperelliptic surface 227 229
Hypergeometric equation 303Ч308
Icosahedral group 129
Improperly discontinuous groups 36
Ince, E. L. 284
Indicial equation 294
Infinitesimal transformations 35
Infinity, point at 2 7 75Ч77 165 293 299 309
Integral, PoissonТs 177Ч179
Inverse of linear transformation 2 5 25 33
Inverse of quotient of solutions of differential equation 287Ч293
Inverse points with respect to circle 10Ч12 19 20 29
Inverse points with respect to sphere 117 119
Inversion in circle 10Ч15 26 28 29 45 104 137 202 280 282 305Ч 308
Inversion in sphere 117Ч119
Isometric circles 23Ч30
Isometric circles, and fixed circles 28Ч30
Isometric circles, and theta series 104 114
Isometric circles, deformation of lengths and areas 25
Isometric circles, geometric interpretation of linear transformation 26 27
Isometric circles, of group 39Ч42 67
Isometric circles, of product 40 53
Isometric circles, prescribed circles 57
Isometric circles, types of transformations 27 28
Isomorphic groups 36 218 236
Iterative process 179Ч186
Johansson, S. 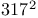
Jordan curve 189
Jordan curves, regions bounded by 198Ч202
K nig, R. 319 nig, R. 319
Kapteyn, W. 314
Kempinski, S. 315
Klein, F. 124 148 311 314 315 317 318 319
Kleinian function 87
Kleinian groups 66
Kluyver, J. C. 315
Koebe, P. 134 140 186 188 191 205 233 262 274 279 288 323
KoebeТs lemma 188
LegendreТs differential equation 304
Levi, E. E. 317
Lewent, L. 323
Lewickyj, W. 321
Lichtenstein, L. 321
Liljestrom, A. 319 320
Limit points of group 41Ч44 46 47 315 58 62Ч64 67Ч69 70 85 108 277
Limit points of regions 205Ч213 216 218 268Ч271
Limit points of regions, application in uniformization 230 234 235 237 242 245 248 252 253 257 278 280 302
Lindemann, F. 316
Linear transformation 1Ч32
Linear transformation, and circle 8Ч15 32 282
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



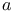 -cuts
-cuts 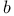 -cuts
-cuts 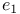 ,
, 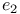 ,
, 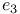
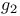 ,
, 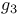
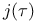
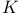

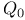
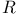 , the region, defined
, the region, defined 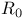
 n, T.
n, T. 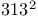
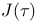
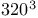
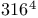
 nig, R.
nig, R.