|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Finkbeiner D.T. Ч Introduction to Matrices and Linear Transformations |
|
|
 |
| ѕредметный указатель |
 -tuples, ordered 209 -tuples, ordered 209
 -tuples, space of 27 35Ч36 42 -tuples, space of 27 35Ч36 42
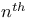 roots of unity 20 124 140 roots of unity 20 124 140
Abstract systems 1Ч22 211Ч212
Abstract systems, homomorphism of 212Ч213 216Ч221
Abstract systems, isomorphism of 212Ч213 217Ч221
Adjoint 97
Adjoint, determinant of 100
Adjoint, method for 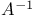 97Ч99 97Ч99
Alias interpretation 60
Alibi interpretation 60
angle 162 173Ч181
Annihilator 76
Associativity 7 16Ч18 49 78
Basis 35Ч39 58Ч59
Basis, change of 121
Basis, dual 76
Basis, for idempotent transformations 62
Basis, for nilpotent transformations 148Ч150
Basis, normal orthogonal 176Ч180 186 189
Basis, of null space 53
Basis, orthogonal 176
BesselТs inequality 178
Bilinear form 163Ч168
Bilinear function 162Ч168
Bilinear function, conjugate 170
Bilinear function, rank of 164
Bilinearity 49 78 170
Binary operation 14 16 211
Binary relation 209Ч210
Binomial coefficient 197
Block multiplication 80Ч83
Boolean algebra 15
Canonical form 107
Canonical form, for congruence 166Ч 167 187
Canonical form, for equivalence 118 120
Canonical form, for idempotent matrices 125
Canonical form, for nilpotent matrices 152
Canonical form, for row equivalence 115
Canonical form, for similarity 156
Canonical form, for skew-symmetric matrices 166
Canonical form, for symmetric matrices 166Ч167 187
Canonical form, Jordan 153Ч158
Cartesian product 8 162 209
Cauchy inequality 172
Cayley Ч Hamilton theorem see Hamilton Ч Cayley theorem
CayleyТs Theorem 219
Characteristic, equation 128 131 133 135 206
Characteristic, numbers 127
Characteristic, polynomial 128 133 136 157Ч159 185
Characteristic, roots 127
Characteristic, values 126Ч 133 136Ч141 146 155 185Ч191 198Ч202 206-207
Characteristic, vectors 126Ч133 135Ч141 185Ч 186 189 191 201-202
Closed operations 13 17Ч19 49
Cofactor 95
Column index 64
Column vector 71 77 89 177
Combinatorial equivalence 104 222Ч228
Commutative group 19
Commutativity 7 16Ч19 48 68
Complement of a set 6
Complex 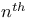 roots of unity 20 124 140 roots of unity 20 124 140
complex numbers 169Ч172 189Ч191
Congruence of integers 219Ч220
Congruence of matrices 165Ч168 180 186Ч 187
Conjugate, -bilinear 170
Conjugate, of a complex matrix 184Ч185 189
Conjugate, of a complex number 169Ч172
Conjugate, symmetry 170
Conjunctivity, of matrices 166 190Ч191
Consistency condition 87
Continuity of a matrix 202
Convergence 193Ч201
Coordinate system 35Ч36 (see also Basis)
Coset, of a function 215 220Ч221
Coset, of a relation 214 220
Cosets, product of 216
CramerТs Rule 98Ч99
Cyclic subspace 145
Dantzig, G. B. 222
Derivative of a matrix 202Ч204
Determinant 88Ч105 127 204
Determinant, cofactor of a 95
Diagonability of matrices 130Ч133 136Ч141 189
Diagonability of quadratic forms 189
Diagonal matrix 69 72 129Ч132 136Ч142 166Ч167 186 189 200
Difference of sets 9
Difference of sets, symmetric 9Ч10
Difference system 217
Differential equation, infinite 36
Differential equation, matric form of 203 206
Differential equation, of a linear algebra 49
Differential equation, of a vector space 38Ч40
Differential equation, of subspaces 39Ч40
Differential equation, solution space of 28 205 207
Dimension, finite 36Ч37
Direct sum 143Ч155
Direction numbers 175
Disjoint sets 6
Distance 162 172Ч173 176Ч179
Distributivity 7 16
Division algebra 51
Division ring 27
Domain of a function 10 210
Domain of a relation 210
Dot product 165 169 176
Dual, basis 76
Dual, operations 7
Dual, space 75Ч76 162
Echelon form 111
Echelon form, reduced 112 226
Eigenvalues 127
Eigenvectors 127
Element 4 13
Element, idempotent 16Ч17
Element, identity 7 16Ч18 219
Element, inverse 16Ч18 219
Elementary divisors 157Ч158
Elementary matrices 108Ч110 223Ч228
Elementary operations on matrices 108Ч 110 117 223Ч228
Elementary operations on systems of equations 101
Equivalence classes 107 213 215 220 224
Equivalence relations 13 104 106Ч125 164Ч168 190Ч191 213Ч215 220 222-228
Equivalence relations, combinatorial equivalence 104 222Ч228
Equivalence relations, congruence 165Ч168 180
Equivalence relations, conjunctivity 166 190Ч191
Equivalence relations, equivalence 117Ч120 122 164Ч165
Equivalence relations, row equivalence 110Ч116
Equivalence relations, similarity 120Ч126 130 136Ч141 151 156 180 186-187
Equivalent matrices 117Ч120 122 164
Equivalent systems of equations 101 116 227
Euclidean group 179
Euclidean space 170 173 175Ч179
Factor system 217
Field 19Ч22 26
Field, as a vector space 28
Field, finite 20 70 166
Field, of scalar matrices 67 72
Finite field 20 70 166
Finite geometry 3
Finite-dimensional 36Ч37
Fixed point 127
Form, bilinear 163Ч168
Form, Hermitian 190Ч 191
Form, quadratic 182Ч191
Forsythe, G. E. 100
Frobenius 51
Function 10Ч13 210Ч211 220-221
Function, coset of a 215Ч216 220Ч221
Function, domain of a 10 210
| Function, of a function 12 45
Function, range of a 10 210
Function, value of a 10
Functions, bilinear 162Ч168
Functions, hermitian 190
Functions, matrices of 202Ч204
Functions, of matrices 195Ч199
Functions, product of 12Ч13
Functions, quadratic 182Ч191
Functions, space of continuous 28 170Ч171
Gram Ч Schmidt orthogonalization 174Ч175 178
Group 18Ч21 26 218Ч221
Group, commutative 19 26 218
Group, euclidean 179
Group, full linear 57
Group, Lorentz 80
Group, of triangular matrices 72
HadamardТs inequality 191
Hamilton 51
Hamilton Ч Cayley theorem 135Ч136 139 158Ч161 195
Hermitian, congruence, see Conjunctivity; Hermitian, form 190Ч191
Hermitian, function 190
Hermitian, matrix 190Ч191
Hermitian, skew 191
Hermitian, symmetry 170
Homogeneous system 86
Homomorphism, kernel of a 52 221
Homomorphism, of abstract systems 212Ч 213 217Ч221
Homomorphism, of vector spaces 41Ч49
Idempotent element 16Ч17
Idempotent linear transformation 48 62 75 143Ч146
Idempotent matrix 70 72 75 125 139
Identity, element 7 16Ч18 219
Identity, linear transformation 46
Identity, matrix 68
Identity, right 21
Independence, see Linear independence Independent vectors, maximal set of 34
Inequality, BesselТs 178
Inequality, Cauchy 172
Inequality, HadamardТs 191
Inequality, Schwarz 171Ч173
Inequality, triangle 173
Infinite-dimensional 36 171
Inner product 169Ч182
Inner product, space 170Ч181
Integral of a matrix 202
Intersection of sets 6 15 17
Intersection of subspaces 30Ч32
Invariant spaces 54 144Ч155
Inverse of a matrix, calculation of, by adjoint method 97Ч99
Inverse of a matrix, calculation of, by approximation 200
Inverse of a matrix, calculation of, by Hamilton Ч Cayley theorem 159Ч161
Inverse of a matrix, calculation of, by pivot operations 103Ч104 227
Inverse of a matrix, calculation of, by row and column operations 118Ч120
Inverse of a matrix, calculation of, by row operations 113Ч114
Inverse of a matrix, calculation of, for an orthogonal matrix 180
Inverse, a linear transformation 56
Inverse, element 16Ч18 219
Inverse, of a mapping 11
Inverse, of a matrix 70 72
Inverse, right 21
Isomorphism, of abstract systems 212Ч213 217Ч221
Isomorphism, of matrices and linear transformations 73Ч76
Isomorphism, of vector spaces 40Ч43
Jordan canonical form 153Ч158 196Ч198 206
Kernel of a homomorphism 52 221
Kronecker delta 68
Latent roots 127
Law of Cosines 177
Left hand notation 45 77 85
Length 162 169 172Ч179
Linear equations, equivalence of 101 116 227
Linear equations, homogeneous 86
Linear equations, non-homogeneous 86
Linear equations, operations on 100Ч105
Linear equations, solution by CramerТs rule 98Ч99
Linear equations, solution of 84 222
Linear equations, system of 84Ч89
Linear transformation 44Ч62
Linear transformation, characteristic values of 126Ч133 136Ч141 146 155 185Ч191 198Ч202 206-207
Linear transformation, characteristic vectors of 126Ч133 135Ч141 185Ч186 191 201-202
Linear transformation, idempotent 48 62 75 143Ч 146
Linear transformation, identity 46
Linear transformation, inverse of 56
Linear transformation, Lorentz 79Ч80
Linear transformation, matric representation of 58Ч64 73 77 121Ч124
Linear transformation, negative 46
Linear transformation, nilpotent 48 54 76 133 142Ч155
Linear transformation, non-singular 55Ч 57 153
Linear transformation, null space of 52Ч54 142 153
Linear transformation, nullity of 52Ч54
Linear transformation, orthogonal 178Ч182 185Ч186
Linear transformation, range space of 52Ч54 114 142 153
Linear transformation, rank of 52Ч54
Linear transformation, restricted to a subspace 144 149 153
Linear transformation, Segre characteristic of 157Ч158
Linear transformation, singular 55
Linear transformation, specific form of 57Ч62
Linear transformation, trace of 160Ч161
Linear transformation, unitary 179 181
Linear transformation, zero 46
Linear transformations, equality of 45
Linear transformations, product of 45Ч46
Linear transformations, scalar multiple of 45Ч 46
Linear transformations, sum of 45Ч46
Linear, algebra 30 49Ч51 73Ч75
Linear, combinations 30
Linear, dependence 32 33
Linear, functional 75Ч76 162
Linear, group 57
Linear, independence 32Ч 39 131Ч132 136 141 146
Linear, programming 101 227
Linear, space; see Vector space Linear equations, consistency condition for 87
Lorentz matrices 79Ч80
Mac Duffee, C. C. 68
Main diagonal 69
Mapping 10Ч13 211Ч221
Mapping, composite 12
Mapping, image under a 10Ч11 211
Mapping, inverse 11
mapping, many-to-one 11 211
Mapping, of a subspace 48
Mapping, one-to- one 11 211
Mapping, reversible 11
Mapping, zero 13
Mappings, product of 13
Mappings, successive 11 21 215Ч217
Markov matrix 79 130
Matric polynomial 134
Matrices, block multiplication of 80Ч83
Matrices, combinatorial equivalence of 104 222Ч228
Matrices, congruence of 165Ч168 180 186Ч187
Matrices, conjunctivity of 166 190Ч191
Matrices, elementary 108Ч110 223Ч228
Matrices, equality of 64
Matrices, equivalence of 117Ч120 122 164Ч165
Matrices, functions of 195Ч199
Matrices, of functions 202Ч 204
Matrices, product of 66 78
Matrices, row equivalence of 110Ч116
Matrices, sequences of 193Ч199
Matrices, similarity of 120Ч126 130 136Ч141 151 156 180 186-187
Matrices, sum of 65
Matrix representing a, bilinear function 164
Matrix representing a, linear transformation 58Ч64 73 77 121Ч124
Matrix representing a, system of equations 84
Matrix, adjoint of 97
Matrix, augmented 86
Matrix, characteristic equation of 128 131 133 135 206
Matrix, characteristic polynomial of 128 133 136 157Ч159 185
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -tuples, ordered
-tuples, ordered 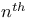 roots of unity
roots of unity