|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Diestel R. — Graph Theory |
|
|
 |
| Предметный указатель |
Edge-chromatic number (see Chromatic index)
Edge-connectivity 11 55 58
Edge-disjoint spanning trees 58—61
Edge-maximal 4
Edge-maximal vs. extremal 149 182
Edge-maximal without 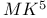 183 183
Edge-maximal without 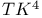 182 182
Edge-maximal without 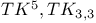 84 84
Edge-maximal without 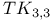 185 185
Edmonds, J. 42 282
Embedding in  69—70 77 69—70 77
Embedding in surface 74 92 274—276 280 281— 282
Embedding in the plane 76 80—93
Embedding of bipartite graphs 202—204
Empty graph 2
End of edge 2 25
End of path 6
Endpoints of arc 68
Endvertex 2 25
Endvertex, terminal vertex 25
Equivalence in quasi-order 277
Equivalence of planar embeddings 76—80 79 90
Equivalence of points in 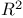 68 68
Erdos — Sos conjecture 152 166 167
Erdos, P. 101 121 151 152 163 166 167 187 197 208 209 210 215 228 232 235—237 243 249 295
Euler, characteristic 276
Euler, formula 7 75 89 90 289
Euler, L. 18—19 74
Euler, tour 19 20 291
Eulerian graph 19
Even, degree 19 33
Even, graph 133 135 145
Event 231
Evolution of random graphs 241 249
Exceptional set 153
Excluded minors (see Forbidden minors)
Existence proof, probabilistic 121 229 233 235—237
Expanding a vertex 113
Expectation 233 234 242
Exterior face (see Outer face)
Externally k-cormcctcd 264 280
Extremal vs. edge-maximal 149 182
Extremal without 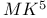 183 183
Extremal without 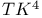 182 182
Extremal without 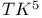 184 184
Extremal without 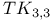 185 185
Extremal, bipartite graph 165
Extremal, graph 1 9—150
Extremal, graph theory 147 151 160 166
Face 70
Factor 29
Factor, 1-factor 29 38
Factor, 1-factor theorem 35 42 66
Factor, 2-factor 33
Factor, k-factor 29
Factor-critical 36 285
Fajtlowicz, S. 187
Fan 55
Fan-version of Menger’s theorem 55
Finite graph 2
First order sentence 239
First point on frontier 68
Five colour theorem 96 121 141
Five colour theorem, list version 106 121
Five-flow conjecture 140 141
Fleischner, H. 218 295
Flow 123—146 125—126
Flow in plane graphs 136—139
Flow, 2-flow, low 133
Flow, 3-low 133—134 141
Flow, 4-low 134—135 140—141
Flow, 6-low theorem 141 143
Flow, conjectures 140—141
Flow, group-valued 128—133 144
Flow, H- flow 128—133
Flow, integral 126 128
Flow, k-flow 131—134 140—143 145
Flow, network flow 125—128 291
Flow, number 131 134 140 144
Flow, polynomial 130 146
Flow, total value of 126
Flow-colouring duality 136—139 291
Forbidden minors and chromatic number 181 185
Forbidden minors and tree-width 263—274
Forbidden minors, expressed by 263 274—277
Forbidden minors, minimal set of 274 280 281
Forbidden minors, planar 264
Forcibly hamiltonian (see Hamiltonian sequence)
Forcing, 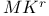 179—184 186 179—184 186
Forcing, 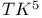 184 187 184 187
Forcing, 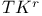 61 170—178 186 61 170—178 186
Forcing, high connectivity 11
Forcing, induced trees 178
Forcing, large chromatic number 101—103
Forcing, linkability 62—63 66 171—174
Forcing, long cycles 8 26 118 213—228
Forcing, long paths 8 166
Forcing, minor with large minimum degree 174 179
Forcing, short cycles 179—180 237
Forcing, subgraph 13 147—167
Forcing, tree 13 178
Forcing, triangle 119 209
Ford, L.R. Jr. 127 145
Forest 12
Forest, minor 281
Forest, partitions 60—61
Four colour problem 120 186
Four colour theorem 96 141 145 181 183 185 215 227
Four colour theorem, history 120—121
Four-flow conjecture 140—141
Frank, A. 65 145
Frobenius, F.G 42
From ... to 6
Frontier 68
Fulkerson, D.R. 122 127 145
Gallai — Edmonds matching theorem 36 38 42
Gallai, T. 39 42 66 167
Galvin, F. 109
Gasparian, G.S. 122
Genus and colouring 121
Genus of a graph 90 280
Genus of a surface 276
Geometric dual (see Plane dual)
Gibbons, A. 145
Gilmore, P.C. 120
girth 7
Girth and average degree 237
Girth and chromatic number 101 121 235—237
Girth and connectivity 237
Girth and diameter 8
Girth and minimum degree 8 179—180 237
Girth and minors 179—180
Girth and planarity 89
Girth and topological minors 178
Godsil, C. 28
Golumbic, M.C. 122
Good, characterization 274 282
Good, pair 252
Good, sequence 252
Gorbunov, K.Yu. 281
Goring, F. 66
Graham, R.L. 210
Graph 2 4 25 26
Graph, invariant 3
Graph, minor theorem 251 274 277 215
Graph, partition 60
Graph, plane 70—76 87—89 96—97 106—108 136—139
Graph, process 250
Graph, property 238
Graph, simple 26
| Graph-theoretical isomorphism 77—78
Graphic sequence (see Degree sequence)
Greedy algorithm 98 108 117
grid 90 184 258
Grid, minor 260 264 274
Grid, theorem 264
Grid, tree-width of 260 278 281
Griinwald, T. 66
Grotzsch, H. 97 141 145
Group-valued flow 128—133
Guthrie, F. 120
Gyarfas, A. 178 185
Hadwiger, H. 181 186 187
Hadwiger, H., conjecture 169—170 181—183 185 186—187
Hajnal, A. 197 210
Hajos, G. 102 187
Hajos, G., construction 101—102
Haken, W. 121
Halin, R. 65—66 227 280—281
Hall, P. 31 42
Hamilton closure 226
Hamilton cycle 213 228
Hamilton cycle and 4—flows 144 215
Hamilton cycle and degree sequence 216—218 226
Hamilton cycle and minimum degree 214
Hamilton cycle and the four colour theorem 215
Hamilton cycle in 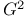 218—226 218—226
Hamilton cycle in 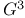 227 227
Hamilton cycle in almost all graphs 241
Hamilton cycle in planar graphs 215
Hamilton cycle, power of 226
Hamilton cycle, sufficient conditions 213—218
Hamilton path 213 218
Hamilton, W.R. 227
Hamiltonian, graph 213
Hamiltonian, sequence 216
Harant, J. 66
head (see Terminal vertex)
Heawood, P.J. 121 145
Heesch, H. 121
Hereditary graph property 263 274—277
Hereditary graph property, algorithmic decidability 276—277
Higman, D.G. 252 280
Hoffman, A.J. 120
Hypergraph 25
In (a graph) 7
incidence 2
Incidence, encoding of planar embedding (see Combinatorial isomorphism)
Incidence, map 25 26
Incidence, matrix 24
incident 2 72
Increasing property 241 248
Independence number 110—117
Independence number and connectivity 214—215
Independence number and Hamilton cycles 215
Independence number and long cycles 118
Independence number and path cover 39
Independence number of random graph 232 248
Independent, edges 3 29—38
Independent, events 231
Independent, paths 7 55 56—57 283
Independent, vertices 3 39 110 232
Indicator random variable 234 295
Induced subgraph 3 111 116—117 290
Induced subgraph in Ramsey theory 196—206
Induced subgraph in random graph 232 249
Induced subgraph of all imperfect graphs 116—117 120
Induced subgraph of all large connected graphs 207
Induced subgraph of almost all graphs 238 248
Induced subgraph, cycle 7—8 21 47 75 86 111 117 290
Induced subgraph, tree 178
Infinite graphs ix 2 28 41 166 209 248 280
Infinity lemma 192 210 294
Initial vertex 25
Inner face 70
Inner vertex 6
Integral, flow 126 128
Integral, function 126
Integral, random variable 242
Interior of a path, P 6—7
Interior of an arc 68
Internally disjoint (see Independent)
Intersection 3
Intersection, graph 279
Interval graph 120 279
INTO 255
Intuition 70 231
Invariant 3
Irreducible graph 219
Isolated vertex 5 248
Isomorphic 3
Isomorphism 3
Isomorphism of plane graphs 76—80
Isthmus (see Bridge)
Jaeger, F. 146
Janson, S. 249
Jensen, T.R. 120 146 281
Johnson, D. 282
Join 2
Jordan, C. 68 70
Jung, H.A. 62 186
k-choosable 105
k-chromatic 95
k-colourable 95
k-constructible 101—102 118
k-mesh 265
k-set 1
Kahn, J. 122
Karoriski, M. 249
Kempe, A.B. 121 227
Kernel of directed graph 108—109 119
Kernel of incidence matrix 24
Kirchhoff’s law 123 124
Klein four-group 135
Kleitman, D.J. 121
Knot theory 146
Knotless graph 211
Kohayakawa, Y. 167
Kollar, J. 167
Komlos, J. 167 110 186 210 226
Konig, D. 30 42 52 103 119 192 210
Konig, D., duality theorem 30 39 111
Konig, D., infinity lemma 192 210 294
Konigsberg bridges 19
Kostochka, A.V. 119
Kruskal, J.A. 253 280 296
Kuratowski, C. 80—84 274
Kuratowski-type characterization 90 274—275 281—282
Larman, D.G. 62
Latin square 119
Leaf 12 27
Lean tree-decomposition 261
Length of a cycle 7
Length of a path 6 8
Length of a walk 9
Line (edge) 2
Line (edge), graph 4 96 185
Linear algebra 20—25 47—49 85—86 116
Linear programming 145
Linked by a path 6
Linked by an arc 68
Linked k-linked 61—63 66
Linked vs. k-connected 62 65
Linked, set 110
Linked, tree-decomposition 261
Linked, vertices 6 68
List, bipartite graphs 108—110 119
List, Brooks’s theorem 121
List, colouring 105—110 121—122
List, conjecture 108 119 122
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте