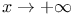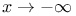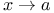|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hardy G.H. — A course of pure mathematics |
|
|
 |
| Предметный указатель |
Abel's test for convergence 329
Abel's theorem on the multiplication of series 339
Algebraical functions: differentiation of 200 217
Algebraical functions: explicit 41
Algebraical functions: implicit 42
Algebraical functions: integration of 226 et seq. 246
Algebraical numbers: see Numbers, algebraical Amplitude of a complex number 82
Areas of curves 236 et seq. 239 249
Areas of curves in polar coordinates 241
Areas of curves, proof of existence of 271 et seq.
Argand diagram 81
Argument of a function 377
Argument of a point 82
Axes of a conic 63 212
Axes of coordinates 29 51
Axes of coordinates, change of 29 et seq.
Binomial theorem 256 288 334 365 368 405
Cauchy's tests for convergence: condensation test 308
Cauchy's tests for convergence: general test 297
Cauchy's tests for convergence: integral test 303 305
Cis  , defined 83 , defined 83
Classes, finite and infinite 110
Coaxal circles 89
Comparison theorems for integrals 311 319
Comparison theorems for series 297 325
Condition that four points lie on a circle 92 93
Condition that three points lie on a straight line 88
Cone 58
Conjugate complex numbers 77
Contact of plane curves 259 et seq.
Continuity 171 et seq.
Continuity of cos x and sin x 174
Continuity of functions of two variables 182
Continuity of polynomials and rational functions 173
Continuity of sums and products 173
Continuity, geometrical illustration of 173
Continuous functions without derivatives 187 et seq.
Continuum, the 15 et seq.
Contour maps 57
Convergence, circle and radius of 333
Convergent and divergent 309 et seq.
coordinates 29 51
Coordinates, polar 34
Cos 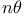 and sin and sin 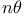 , applications 97 98 104 , applications 97 98 104
Cos 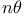 and sin and sin 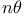 , formulae for 95 et seq. 103 , formulae for 95 et seq. 103
Cos x, sin x, series for 255 400
Cross ratios 92
Curvature 261 291
Cylinder 56
d'Alembert's test for convergence 298
De Moivre's theorem 82 et seq. 101 390
De Moivre's theorem, applications 96 et seq. 103
Decimals, terminating 3
Derivative 185 et seq.
Derivative of 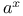 351 351
Derivative of 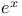 349 349
Derivative of 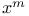 190 199 351 190 199 351
Derivative of a complex function 194
Derivative of a constant 190
Derivative of a determinant 242
Derivative of a function of a function 216
Derivative of a function of two functions 264 et seq.
Derivative of a polynomial 196 et seq.
Derivative of a rational function 198 et seq.
Derivative of a sum, a product, etc. 192 et seq. 195
Derivative of a transcendental function 200 et seq. 217
Derivative of an algebraical function 200 217
Derivative of an inverse function 194 195
Derivative of arc sin x, etc. 196 201
Derivative of cos x and sin x 190
Derivative of exp{(a+ib)x} 40824
Derivative of f(ax+b) 193
Derivative of log x 343
Derivative of tan x, etc. 200
Derivative, meaning of sign of 205
Derivatives of 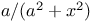 and and 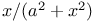 204 204
Derivatives of 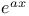 , etc. 353 , etc. 353
Derivatives of functions of several variables 262 et seq.
Derivatives, higher 202 et seq.
Derivatives: discontinuous 213
Derivatives: general theorems concerning 205 et seq.
Difference-equations 337
Differential coefficient 187
Differential equations: 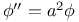 249 371 249 371
Differential equations: of straight lines, circles, etc. 242 243
Differential, partial 263
Differential, repeated 202 et seq.
Differential, total 264; see also “Derivative”
Dirichlet's test for convergence 328
Dirichlet's theorem on the rearrangement of series 301 324 330
Discontinuity, types of 175
Displacements 66 et seq.
Double limit problems 420 et seq.
e, number 347 et seq.
Equation of a circle 32 61
Equation of a cone 58
Equation of a conic 63
Equation of a cylinder 56
Equation of a locus in a plane 30 et seq. 53
Equation of a locus in space 51 et seq.
Equation of a plane 52
Equation of a ruled surface 59
Equation of a sphere 53
Equation of a straight line 30
Equation of a surface in general 55
Equation of a surface of revolution 58
Equation with complex coefficients 89 102
Equation x=f(x) 155
Equation, complete 384
Equation, cubic or biquadratic 15 et seq. 42 60 102
Equation, general: of first degree 31 52
Equation, general: of second degree 63
Equation, quadratic: complex roots of 79
Equation, quadratic: geometrical construction for roots of 8
Equation, quadratic: graphical solution of 50
Equation, quadratic: with complex coefficients 88 102
Equation, repeated roots of 197 243
Equations, algebraical: approximation to roots of, by Newton's method 253
Equations, algebraical: graphical solution of 51 60
Equations, algebraical: number of roots of 80 415
Equations, algebraical: proof of existence of roots of 415 et seq.
Equations, algebraical: rational roots of 7 20
Equations, algebraical: repeated roots of 197 209 243
Equations, algebraical: with complex coefficients, cubic 89
Equations, algebraical: with complex coefficients, linear 88
Equations, algebraical: with complex coefficients, quadratic 88 102
Equations, algebraical: with rational coefficients, irrational roots occur in pairs 11 86
Equations, algebraical: with real coefficients, complex roots occur in pairs 85
Equations, differential see “Differential equations”
Equations, functional 292 344 344 349 350 371 384 388
Equations, transcendental 51 61 201 209 244 254 354 371 396 et 408
Equations: of a line or curve in space 55
Equations: of a section of a cone 62
Equations: of the tangent and normal to a curve 190 218
Euler's 359 369
Euler's constant 359
Euler's theorem on homogeneous functions 291
Expansions see “Power-series”
Exponential function 348 et seq. 386
Exponential function, continuity of 349 367 387
Exponential function, derivative of 349 367
Exponential function, functional equation satisfied by 349 388
Exponential function, graph of 349
Exponential function, integrals involving 353 et seq.
Exponential function, order of infinity of, as 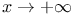 350 356 369 372 350 356 369 372
Exponential function, power-series for 360 et seq. 399
Exponential function, representation of, as a limit 351 et seq. 393
Exponential limit 140 et seq. 154 351 393
Exponential series 300 331 335 360 373 399
Exponential theorem 361
| Exponential values of cos x and sin x 394
Factor theorem for complex numbers 77
Formulae of reduction 247 et seq. 316 354
Fourier's integrals 280
Function of several variables 182
Function, attains its upper and lower limits 181
Function, continuous 171 et seq.
Function, fundamental property of 175
Function, range of values of 180 et seq.
Functions see also “Algebraical functions” “Exponential “Function continuous” “Logarithmic “Oscillation” “Polynomials” “Rational
Functions in stricter sense 179
Functions of a continuous real variable. 25 et seq.
Functions of a positive integral variable 108 et seq.
Functions of several variables 51 et seq.
Functions, 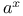 350 et seq. 388 350 et seq. 388
Functions, algebraical, explicit 41
Functions, algebraical, implicit 42
Functions, algebraical, transcendental 44 et seq.
Functions, complex, of a real variable 94
Functions, exponential 348 et seq. 386
Functions, expression of as limits 149 150 155
Functions, graphical representation of 28 et seq. 51
Functions, homogeneous 291
Functions, hyperbolic 355 395
Functions, hyperbolic, inverse 356
Functions, increasing and decreasing 135 et seq. 162 171
Functions, independent and non-independent 270
Functions, inverse 178 et seq.
Functions, logarithmic 222 et seq. 342 380 392
Functions, of a complex variable 376 et seq.
Functions, rational 38 et seq.
Functions, trigonometrical or circular 44 et seq. 394
Functions, trigonometrical or circular, inverse 45 et seq. 398
Geometrical allied series 148 et seq. 154 156 299
Geometrical series 145 et seq. 153
Geometrical series, rapidity of convergence of 303
Geometrical series, tests of convergence derived from comparison with 297 et seq.
Harmonic relation of four points 92
homogeneous functions 291
Hyperbolic functions 355 395
Hyperbolic functions, inverse 356
Inequalities 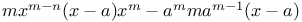 165 165
Infinite 146 et seq.
infinity 114 et seq.
Infinity of a function 174 175
Infinity scales of, logarithmic and exponential 346 350 370
Inflexion, point of 260
Integral function 220
Integral function, 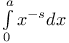 317 et seq. 317 et seq.
Integral function, 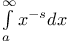 307 312 307 312
Integral function, indefinite 278
Integral, approximation to 295
Integral, calculation of, from indefinite integral 279
Integral, curvilinear 377 et seq.
Integral, definite 277 et seq.
Integral, direct 280
Integral, finite 310
Integral, general properties of 281 et seq.
Integral, infinite, of first kind 309 et seq.
Integral, limits of 278
Integral, of second kind 316 et seq.
Integrals connected with conics 227 et seq. 246 250
Integration 219 et seq.
Integration 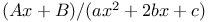 , explicit 224 , explicit 224
Integration by parts 230 234 247
Integration by parts for definite integrals, finite 284 et seq. 287
Integration by parts for definite integrals, infinite 316 320
Integration by substitution 226 et seq. 231 234 246 354
Integration by substitution for definite integrals, finite 284 et seq.
Integration by substitution for definite integrals, finite, infinite 314 et seq. 320 321
Integration of 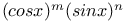 , etc. 233 248 , etc. 233 248
Integration of 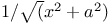 , etc. 229 , etc. 229
Integration of 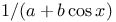 , etc. 235 249 , etc. 235 249
Integration of $exp \{ (a+ib)x \}$408
Integration of 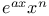 , etc. 354 , etc. 354
Integration of 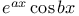 , etc. 353 et seq. , etc. 353 et seq.
Integration of 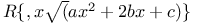 228 et seq. 246 228 et seq. 246
Integration of 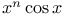 , etc. 233 248 , etc. 233 248
Integration of 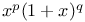 232 248 232 248
Integration of 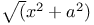 , etc. 231 , etc. 231
Integration of algebraical functions 226 et seq. 246
Integration of arc sin, etc. 235 et seq.
Integration of log x, etc. 235 et seq. 249
Integration of polynomials 222
Integration of R (cos x, sin x) 234 et seq.
Integration of rational functions 222 et seq. 247
Integration of tan x, etc. 234 248
Integration of transcendental functions 233 et seq.
Integration of trigonometrical functions 233 et seq.
Integration, explicit 225
Integration, path of 378
Integration, range of 278
Integration, subject of 278
Integration: arbitrary constant of 221
Interpolation, functional 109
Irrational numbers see “Numbers” “irrational”
Jacobians 270
Leibniz's theorem 202
Lengths of curves 238 et seq.
Lengths of curves in polar coordinates 241
Lengths of curves, existence of 276
Level curves 412 et seq.
Limit and value 121 166
Limit as  of of 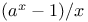 350 351 350 351
Limit as  of (sin x)/x, etc. 169 et seq. of (sin x)/x, etc. 169 et seq.
Limit as  of {log(l+x)}/x 344 392 of {log(l+x)}/x 344 392
Limit as 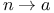 of of 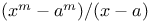 168 168
Limit as 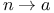 of of 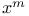 165 166 173 165 166 173
Limit as 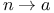 of P(x), R(x) 165 of P(x), R(x) 165
Limit as  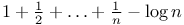 , etc. 359 369 , etc. 359 369
Limit as  of of 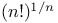 140 140
Limit as  of of 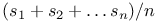 158 158
Limit as  of of 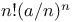 370 370
Limit as  of of 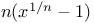 141 et seq. 352 141 et seq. 352
Limit as  of of 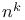 122 122
Limit as  of of 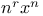 , , 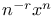 140 140
Limit as  of of 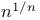 140 140
Limit as  of of 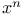 138 153 138 153
Limit as  of of 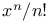 140 140
Limit as  of of 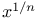 140 140
Limit as  of of 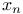 , where , where 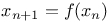 155 155
Limit as  of of ![$\sqrt [n] {(n!)/n}$](/math_tex/ad22fef801af557d73ff431fcbe2433682.gif) 356 356
Limit as  of of 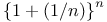 140 et seq. 154 140 et seq. 154
Limit as  of of 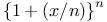 351 et seq. 393 351 et seq. 393
Limit as  of of 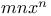 155 155
Limit as  of f(n+1)-f(n) and {f(n)}/n 158 of f(n+1)-f(n) and {f(n)}/n 158
Limit as  of R (n) and of R (n) and 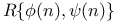 134 et seq. 134 et seq.
Limit as  of {f(n+1)}/{f(n)} and of {f(n+1)}/{f(n)} and ![$\sqrt[n] {\{ f(n) \}} $](/math_tex/9367a6eda6d0cc38705987b01251c59c82.gif) 356 356
Limit as 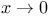 of of 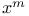 165 168 165 168
Limit of a complex function 151 et seq.
Limit of a function of a complex variable 393
Limit of a sum, a product, etc. 127 et seq. 161 164
Limit of an increasing or decreasing function 135 et seq. 162 171
Limit of f(x), as 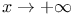 159 et seq. 159 et seq.
Limit of f(x), as 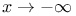 160 160
Limit of f(x), as 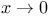 162 162
Limit of f(x), as 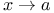 163 163
Limit, calculation of by differentiation 257 et seq.
Limit, exponential 140 et seq. 154 351 393
Limit, logarithmic 141 et seq. 352
Limit, upper and lower, of a function 180 et seq.
Limit, upper and lower, of an integral 278
Limit: of f(n), as  116 et seq. 116 et seq.
Limits, geometrical illustrations of definitions of 119 161
Locus in a plane 31 et seq.
Locus in space 54 et seq.
Logarithm 342 et seq.; see also “Logarithmic function” “Logarithmic “Logarithmic
Logarithm of a complex number 380 et seq.
Logarithm of a complex number to any base 392
Logarithm of a negative number 384 385
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 , defined
, defined 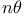 and sin
and sin 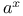
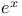
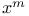
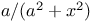 and
and 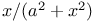
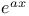 , etc.
, etc. 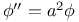
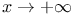
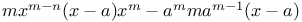
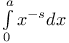
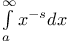
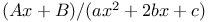 , explicit
, explicit 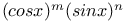 , etc.
, etc. 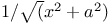 , etc.
, etc. 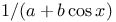 , etc.
, etc. 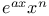 , etc.
, etc. 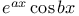 , etc.
, etc. 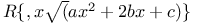
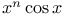 , etc.
, etc. 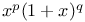
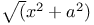 , etc.
, etc.  of
of 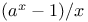
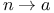 of
of 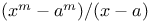

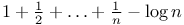 , etc.
, etc. 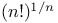
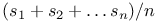
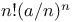
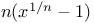
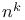
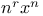 ,
, 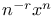
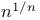
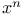
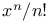
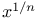
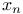 , where
, where 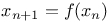
![$\sqrt [n] {(n!)/n}$](/math_tex/ad22fef801af557d73ff431fcbe2433682.gif)
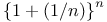
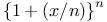
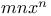
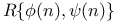
![$\sqrt[n] {\{ f(n) \}} $](/math_tex/9367a6eda6d0cc38705987b01251c59c82.gif)
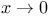 of
of