|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hardy G.H. — A course of pure mathematics |
|
|
 |
| Предметный указатель |
Logarithm, common 353
Logarithm, principal value of 382
Logarithmic function 222 et seq. 341 380 392
Logarithmic function and inverse trigonometrical functions 398 et seq.
Logarithmic function, functional equation satisfied by 344 384
Logarithmic function, graph of 343
Logarithmic function, order of infinity of, as 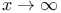 344 et seq. 369 373 344 et seq. 369 373
Logarithmic function, power-series for 363 et seq. 402
Logarithmic function, representation of, as a limit 142 352
Logarithmic limit 142 352
Logarithmic scale of infinity 346
Logarithmic series 363 et seq. 402
Logarithmic tests for convergence 357 et seq.
Maclaurin's integral test for convergence 303 305
Maclaurin's series 255; see also “Taylor's series”
Maxima and minima 206 et seq. 256
Maxima and minima of  210 et seq. 210 et seq.
Maxima and minima, discrimination between 207 257
Maxima and minima, examples of 209 et seq. 244
Maxima and minima, occur alternately 208
Mean value theorem 214 et seq.
Mean Value Theorem for functions of two variables 267
Mean Value Theorem for integrals, Bonnet's form 286
Mean Value Theorem for integrals, first 282
Mean Value Theorem for integrals, generalised 282
Mean Value Theorem for integrals, second 285
Mean Value Theorem of second order 252
Mean Value Theorem, general 252
Measure of curvature 261
Mercator's projection 410
Modulus 82
Modulus of a product 83
Modulus of a sum 84 86 324
Multiplication of series 301 et seq. 334 335 339 373
Newton's method of approximation to the roots of an equation 253
Normal to a curve 190 218
Number  17 65 17 65
Number  5 et seq. 12 5 et seq. 12
Number e 347 et seq.
Number i 77 et seq.
Number, complex 75 et seq.
Number, complex, conjugate 77
Number, complex, equivalence, addition, multiplication and division of 75 et seq.
Number, complex, factor theorem for 77
Number, complex, geometrical applications of 86 et seq. 101
Number, complex, modulus and amplitude of 82
Number, complex, rational functions of 84 et seq.
Number, complex, real and imaginary parts of 82
Number, complex, roots of 98 et seq.
Number, complex, trigonometrical applications of 95 et seq.
Number, infinite 111 et seq.
Numbers, algebraical 23 et seq.;see also “Numbers irrational” “Quadratic “Surds”
Numbers, irrational 4 et seq.; see also “Numbers algebraical” “Quadratic “Surds”
Numbers, irrational, expression of as decimals 147
Numbers, rational 1 et seq.
Numbers, rational, expression of as decimals 3 146
Orders of smallness and greatness 168 et seq. 183 344 350
Oscillation of  , etc. 125 , etc. 125
Oscillation of a function of n 123 et seq.
Oscillation, examples of 124 et seq.
Oscillation, finite and infinite 124
Oscillation, of a function of x 160 et seq.
Oscillation, theorems connected with 126 129
Partial fractions 198 et seq. 222
Polygons, regular, constructions for 100
Polynomials 35 et seq.
Polynomials in a complex variable 80
Polynomials, continuity of 173
Polynomials, differentiation of 196 et seq.
Polynomials, having given values 61
Polynomials, in x, 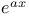 , etc., integration of 354 , etc., integration of 354
Polynomials, in x, cos ax, etc., integration of 233 et seq. 248
Polynomials, in x, log x, etc., integration of 236 249
Polynomials, integration of 222
Polynomials, limits of, as 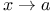 165 165
Power-series 331 et seq.
Power-series, circle and radius of convergence of 332 et seq.
Power-series, multiplication of 334
Power-series, recurring 337 et seq.
Power-series, uniqueness of 333
Power-series: Taylor's and Maclaurin's 255 287
Power-series: Taylor's and Maclaurin's for arc tan x 364 404; “Exponential “Logarithmic
Power-series: Taylor's and Maclaurin's for cos x and sin x 255 400
Principal value, of  390 390
Principal value, of 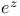 391 391
Principal value, of am z 82
| Principal value, of Log z 382
Pringsheim's theorem 304 et seq. 309
Pringsheim's theorem, analogue of, for integrals 314
Quadratic surds 5 et seq.
Quadratic surds, approximation to, by binomial theorem 366
Quadratic surds, geometrical constructions for 8 et seq. 64
Quadratic surds, theorems concerning 9 et seq.
Quadrature of circle, approximate 65
Radius of convergence 333
Radius of curvature 261
Rates of variation 188 et seq.
Rational functions 38 et seq. 61
Rational functions of 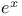 , integration of 354 , integration of 354
Rational functions of 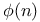 , , 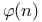 , etc., limits of, as , etc., limits of, as 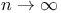 134 134
Rational functions of a complex variable 84 et seq.
Rational functions of cos x and sinx, integration of 234
Rational functions of n, limits of, as 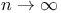 135 135
Rational functions of x, limits of, as 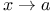 165 165
Rational functions, continuity of 173
Rational functions, differentiation of 198 et seq.
Rational functions, integration of 222 et seq.
Rational numbers see “Numbers” “rational”
Rationalisation, integration by 226 et seq. 231 234 246 354
Rearrangement of series 301 324 327 328 330
Recurring series 337 et seq.
Rolle's theorem in general 205
Rolle's theorem, for polynomials 198
Roots see “Equations”
Scales of infinity 346 350 370
Series, infinite 142 et seq. 296 322 “Exponential “Geometrical “Logarithmic “Multiplication “Power-series” “Rearrangement “Taylor's
Series, infinite, arithmetic 148
Series, infinite, convergence, divergence, and oscillation of 143
Series, infinite, general theorems concerning 144 et seq.
Series, infinite, harmonic 144 149 300 305 308 335 359 369
Series, infinite, of complex terms 330 et seq.
Series, infinite, of complex terms, absolutely convergent 330
Series, infinite, of positive and negative terms 322 et seq.
Series, infinite, of positive and negative terms, Abel's and Dirichlet's tests of convergence for 328 et seq.
Series, infinite, of positive and negative terms, absolutely convergent 323 et seq.
Series, infinite, of positive and negative terms, alternating 326
Series, infinite, of positive and negative terms, conditionally convergent 325 et seq.
Series, infinite, of positive terms 145 296
Series, infinite, of positive terms Cauchy's and d'Alembert's tests of convergence for 297 et seq.
Series, infinite, of positive terms comparison theorem for 297
Series, infinite, of positive terms condensation test of convergence for 308
Series, infinite, of positive terms integral test of convergence for 305 et seq.
Series, infinite, of positive terms Pringsheim's theorem concerning 304 et seq.
Series, infinite, special:  364 404 364 404
Series, infinite, special:  , ,  , etc. 404 414 , etc. 404 414
Series, infinite, special:  , ,  324 328 329 324 328 329
Series, infinite, special:  8 299 307 309 8 299 307 309
Series, infinite, special:  362 362
Series, infinite, special: 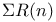 299 335 299 335
Series, infinite, special:  , ,  153 154 153 154
Series, infinite, special:  , ,  , , 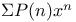 , ,  , ,  , ,  , ,  , ,  , ,  , ,  see other entries mentioned see other entries mentioned
Series, infinite, special:  , ,  144 149 300 305 308 335 359 369 144 149 300 305 308 335 359 369
Series, infinite, special:  156 299 156 299
Series, infinite, special:  367 367
Simpson's rule 295
Stereographic projection 410
Surds 14 et seq. 21
Surds, approximation to, by binomial theorem 366; see also “Numbers algebraical” “Quadratic
surface 54
Surface of revolution 58
Surface, ruled 59
Symmetric functions of the roots of a trigonometrical equation 96 et seq.
Tangent to a curve 185 et seq.
Tangent to a curve, equation of 190 218
Taylor's series 255 287
Taylor's series for derivative or integral 373
Taylor's series, remainder, Cauchy's form 288
Taylor's series, remainder, Lagrange's form 255
Taylor's theorem 252 et seq. 287
Transformation 90 et seq. 104 409
Transformation  105 105
Transformation  , ,  etc. 409 et seq. etc. 409 et seq.
Transformation  411 411
Transformation  94 94
Transformation  105 105
Transformation z=(aZ+b)/(cZ+d) 90 et seq. 104
Triangles, geometrical properties of 86 87 101 419
Unity, roots of 99 et seq.
Variable, continuous real 18 et seq.
Variable, positive integral 19 108
Velocity 189
“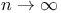 ” 114 et seq. ” 114 et seq.
“Large values'” of n 111 et seq.
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



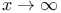



 , etc.
, etc. 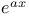 , etc., integration of
, etc., integration of 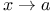

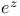
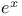 , integration of
, integration of 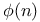 ,
, 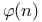 , etc., limits of, as
, etc., limits of, as 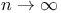

 ,
,  , etc.
, etc.  ,
, 


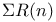
 ,
, 
 ,
,  ,
, 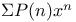 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
 ,
, 



 ,
,  etc.
etc. 

