|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ryser H.J. — Combinatorial Mathematics |
|
|
 |
| Предметный указатель |
Minimal permanent 59 77 124
Minimal term rank 70 75
Minimal trace 76
Monotone column sum vector 61
Monotone row sum vector 61
Montmort 23
Moore, E. H 127 129
Multinomial coefficient 11
Multiplicative law 26
Multiplicity 7
Multiplier 135ff.
Multiplier, conjectures on 139
Multiplier, examples of 139 140
Multiplier, group 136
Multiplier, theorems 137 139
Nagell, T. 28 127 129
Netto, E. 16 127 129
Newman, M. 59 60 129
Nikolai, P. J. 127 129
Nonexistence theorem for (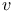 , ,  , ,  )-configurations 111 )-configurations 111
Nonexistence theorem for finite planes 93 94 115
Normal matrix 103
Normalized class 69
Normalized form of matrix 118
Normalized Hadamard matrix 105
Normalized Latin rectangle 35
Null set 4
One to one mapping 6
One to one mapping, in projective plane 90
Order of finite plane 91
Order of group 7
Order of Kirkman system 101
Order of Latin square 36
Order of square array 24
Order of Steiner system 99
Ordered  -tuple see Sample -tuple see Sample
Ordered partition 4
Ordinary line 93
Ordinary point 93
Ore, O. 60
Orthogonal Latin squares 79ff.
Orthogonal Latin squares, and finite planes 92
Orthogonal Latin squares, as an array 82
Orthogonal Latin squares, complete set 80
Orthogonal Latin squares, Euler conjecture on 84ff.
Orthogonal Latin squares, existence theorems for 81ff.
Orthogonal Latin squares, for 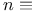 10 (mod 12) 85 10 (mod 12) 85
Orthogonal set see Orthogonal Latin squares
Ostrom, T. G. 141
Paley, R. E. A. C. 127 129
Parker, E. T. 85 94 95 129
Partition of set 4
Partition of set, (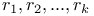 ) repartition 10 ) repartition 10
Partition of set, ordered 4
Partition of set, unordered 4
Pascal triangle 14
Perfect difference set 131ff.
Perfect difference set, and circulant 131
Perfect difference set, and Hadamard configuration 133
Perfect difference set, conjectures on 132 139
Perfect difference set, examples of 139 140
Perfect difference set, fixing of 139
Perfect difference set, isomorphism of 135
Perfect difference set, multiplier of 135ff.
Perfect difference set, planar 132
Perfect difference set, survey of 133
Permanent 25ff.
Permanent, conjectures on 59 77 124
Permanent, formula for 26
Permanent, of circulant 125
Permanent, of incidence matrix 54 124
Permutation 5
Permutation matrix 54
Pickert, G. 95
Pigeon-hole principle 38
Planar difference set 132
Planar difference set, table for 132
Point 89
Point, ideal 93
Point, ordinary 93
Polynomial congruence 136
Prime 13
Principle of duality 90
Principle of inclusion and exclusion 18
Principle submatrix 44
Probl me des m me des m nages 32 nages 32
Probl me des recontres 23 me des recontres 23
Problem of 36 officers 1 84
Problem of dance 58
Problem of Montmort 23
Problem of rooks 24
Problem of schoolgirls 1 101
Problem of weights 1
Product set 5
Projective plane 89ff.
Projective plane, duality in 90
Projective plane, finite 91ff.
Projective plane, incidence relation in 89
Projective plane, line of 89
Projective plane, one to one mapping in 90
Projective plane, point of 89
Proper subset 4
Quadratic form 108
Quadratic form, congruence of 109
Quadratic form, of matrix 108
Quadratic nonresidue 114
Quadratic residue 114
Rado, R. 46 60
Ramsey, F. P. 38 46
Ramsey’s theorem 38ff.
Ramsey’s theorem, applications 43ff.
rectangular array 24
Rectangular array, main diagonal of 25
Rectangular array, position in 24
Rectangular array, size of 24
Rectangular array, square 24
Rectangular array, subarray of 24
Rectangular array, symmetric 25
Rectangular array, transpose of 25
Recurrence 29
Recurrence inequality 41
| Reiss, M. 100 127 129
Relatively prime 19 20
Replications 97
Representative 47
Richardson, M. 129
Right coset decomposition 51
Riordan, J. 16 28 29 36 37
Rooks 24
Rouse Ball, W. W. 127 130
Row by column rule 25
Row sum vector 61
Row sum vector, monotone 61
Rule of product 5
Rule of sum 4
Ryser, H. J. 59 60 78 93 94 95 127 128 130 141
Sade, A. 37
Sample 5
Sample,  -sample 5 -sample 5
Sample, size of 5
Sch tzenberger, M. P. 130 tzenberger, M. P. 130
Secondary diagonal 71
Selection see Unordered selection
Set 3
Set,  -set 4 -set 4
Set, disjoint 4
Set, element of 3
Set, finite 4
Set, intersection of 4
Set, null 4
Set, of  elements 4 elements 4
Set, partition of 4
Set, proper subset of 4
Set, subset of 3
Set, union of 4
Shrikhande, S. S. 85 94 95 130
Sieve formula 19
Sieve of Eratosthenes 22
Silverman, R. 130
Singer, J. 132 141
Size of array 24
Size of sample 5
Size of unordered selection 7
Skolem, T. 46 127 130
Skornyakov, L. A. 95
Sprott, D. A. 130 141
Square array 24
Square array, order of 24
Squarefree 93
Squarefree part 93
Stanton, R. G. 141
Steiner triple system 99
Steiner triple system, number of 100 101
Steiner triple system, order of 99
Stevens, W. L. 94 95
Storer, J. 141
Straus, E. G. 129
subarray 24
Subset 3
Subset,  -subset 4 -subset 4
Subset, proper 4
Swift, J. D. 127 128
Sylvester 19 109
Symmetric array 25
Symmetric group 6
Symmetric group, degree of 6
Symmetrical balanced incomplete block design see (
System of common representatives 50ff.
System of common representatives, application to cosets 51
System of common representatives, fundamental theorem on 50
System of distinct representatives 47ff.
System of distinct representatives, fundamental theorem on 48
System of distinct representatives, lower bound for 48
Szekeres, G. 46
Table for  37 37
Table for 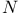 ( (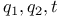 ) 42 ) 42
Table for planar difference sets 132
Tarry, G. 85 94 95
Taussky, O. 127 129 130
Term rank 55ff.
Term rank, fundamental theorem on 55
Term rank, intermediate 70
Term rank, maximal 70ff.
Term rank, minimal 70 75
Term rank, with 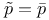 76 76
Tinsley, M. F. 127 130
Todd, J. A. 127 130
Touchard, J. 33 37
Trace 55
Trace, maximal 76
Trace, minimal 76
TRANSPOSE 25
Triple 99
Triple system of Kirkman 101
Triple system of Steiner 99
Turyn, R. 141
Unessential 1 71
Union of sets 4
Unordered collection see Unordered selection
Unordered partition 4
Unordered selection 7
Unordered selection,  -selection 7 -selection 7
Unordered selection, multiplicity of 7
Unordered selection, size of 7
Van der Waerden conjecture 59 77 124
Varieties 96
Vaughan, H. E. 59
Veblen, O. 94 95
Walker, R. J. 127 128
Weight 17
Welch, L. R. 141
Whaples, G. 59
Whiteman, A. L. 141
Williamson, J. 127 130
Wright, E. M. 28
Yamamoto, K. 36 37
Yates, F. 128
Yu, Chinese Emperor 1
Zero-one matrix 27 53ff. 61ff.
Zero-one matrix, as incidence matrix 53ff.
Zero-one matrix, class of 61ff.
Zero-one matrix, complement of 98
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ,
,  ,
,  )-configurations
)-configurations  -tuple
-tuple 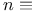 10 (mod 12)
10 (mod 12) 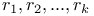 ) repartition
) repartition 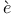 me des m
me des m nages
nages  tzenberger, M. P.
tzenberger, M. P.  -set
-set 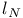
 (
( )
)