|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Munkres J.R. — Analysis on manifolds |
|
|
 |
| Предметный указатель |
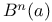 see “n-ball” see “n-ball”
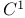 see “Class see “Class 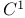 ” ”
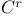 see “Class see “Class 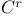 ” ”
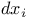 , elementary 1-form 253 , elementary 1-form 253
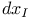 , elementary k-form 254 , elementary k-form 254
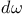 , differential 256 , differential 256
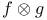 , tensor product 223 , tensor product 223
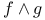 , wedge product 238 , wedge product 238
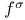 229 229
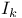 , identity matrix 5 , identity matrix 5
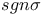 228 228
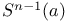 see “n-1 sphere” see “n-1 sphere”
 , symmetric group 227 , symmetric group 227
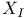 , submatrix 184 , submatrix 184
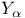 see “Parametrized-manifold” see “Parametrized-manifold”
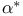 , dual transformation of forms 267 , dual transformation of forms 267
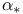 , induced transformation of vectors 246 , induced transformation of vectors 246
 -neighborhood of point 26 -neighborhood of point 26
 -neighborhood of set 34 -neighborhood of set 34
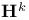 , , 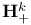 200 200
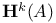 , deRham group 335 , deRham group 335
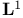 left half-line 283 left half-line 283
 as metric space 25 as metric space 25
 as vector space 2 as vector space 2
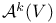 , alternating tensors 229 , alternating tensors 229
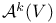 , alternating tensors, basis for 232 , alternating tensors, basis for 232
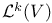 , k-tensors on V 220 , k-tensors on V 220
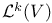 , k-tensors on V, basis for 221 , k-tensors on V, basis for 221
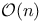 , orthogonal group 209 , orthogonal group 209
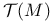 see “Tangent bundle” see “Tangent bundle”
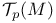 see “Tangent space” see “Tangent space”
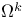 , linear space of k-forms 255 351 , linear space of k-forms 255 351
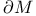 see “Boundary of manifold” see “Boundary of manifold”
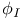 , elementary tensor 221 , elementary tensor 221
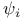 , elementary alternating tensor 232 , elementary alternating tensor 232
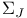 222 222
![$\Sigma_{[I]}$](/math_tex/d7b3d09d3509649f6bb51800910533d982.gif) 184 184
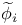 , elementary 1-form 249 , elementary 1-form 249
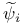 , elementary k-form 249 , elementary k-form 249
Addition of matrices 4
Addition of vectors 1
Additivity of integral 106 109
Additivity of integral (extended) 125
Additivity of volume 112
Alternating tensor 229
Alternating tensor, elementary 232
Antiderivative 99
Approaches as a limit 28
ARC 306
Area 179
Area of 2-sphere 216—217
Area of parametrized-surface 191
Area of torus 217
Ascending k-tuple 184
Ball, 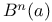 see “n-ball” see “n-ball”
Ball, open 26
Basis 2 10
Basis for  3 3
Basis, usual, for tangent space 249
Bd A 29
Boundary of manifold 205 346
Boundary of manifold, induced orientation 288 346
Boundary of set 29
Bounded set 32
Cauchy — Schwarz inequality 9
Centroid of 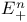 218 218
Centroid of bounded set 168
Centroid of cone 168
Centroid of half-ball 169
Centroid of manifold 218
Centroid of parametrized-manifold 193
Chain rule 56
Change of variables 147
Change of Variables Theorem 148
Change of variables theorem, proof 161
Class 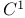 50 50
Class 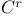 , form 250 351 , form 250 351
Class 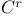 , function 52 144 199 , function 52 144 199
Class 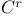 , manifold 196 200 347 , manifold 196 200 347
Class 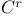 , manifold-boundary 206 , manifold-boundary 206
Class 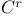 , tensor field 248 , tensor field 248
Class 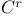 , vector field 247 , vector field 247
Class  52 52
Closed cube 30
Closed form 259
Closed form, not exact 261 308 343
Closed set 26
Closure 26
Cofactors 19
Cofactors, expansion by 23
Column index 4
Column matrix 6
Column rank 7
Column space 7
Common refinement 82
Compact 32
Compact support 139
Compact vs. closed and bounded 33 38
Compactness of interval 32
Compactness of rectangle 37
Comparison property of integral 106
Comparison property of integral (extended) 125
Component function 28
Component interval 81
Components of alternating tensor 233
Components of form 249
Composite function, class 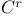 58 58
Composite function, differentiability 56
Cone 168
Connected 38
Connectedness of convex set 39
Connectedness of interval 38
Conservative vector field 323
Content 113
Continuity of algebraic operations 28
Continuity of composites 27
Continuity of projection 28
Continuity of restriction 27
continuous 27
Continuously differentiable 50
Convex 39
Coordinate patch 196 201 346
Coset 334
Covering 32
Cramer’s Rule 21
Cross product 183 313
Cross-section 121
cube 30
Cube, open 26
Curl 264
Cylindrical coordinates 151
d(x,C) 34
Darboux integral 89
deRham group 335
deRham group of 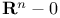 341 341
deRham group of 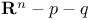 344 344
deRham’s theorem 354
Derivative 41 43
Derivative of composite 56
Derivative of inverse 60
Derivative vs. directional derivative 44
Determinant of product 18
Determinant of transpose 19
Determinant vs. rank 16
Determinant, axioms 15
Determinant, definition 234
Determinant, formula 234
Determinant, geometric interpretation 169
Determinant, properties 16
Df, derivative 43
| df, differential 253 255
Diagonal 36
Diffeomorphism 147
Diffeomorphism of manifolds 347
Diffeomorphism, preserves rectifiability 154
Diffeomorphism, primitive 156
Differentiable 41—43
Differentiable homotopy 325
Differentiable manifold 346
Differentiable vs. continuous 45
Differentiably homotopic 325
Differential form of order 0 251
Differential form on manifold 351
Differential form on open set in  248 248
Differential of 0-form 253
Differential of k-form 256
Differential operator 256
Differential operator as directional derivative 262
Differential operator in manifold 352
Dimension of vector space 2
Directional derivative 42
Directional derivative in manifold 349
Directional derivative vs. continuity 44
Directional derivative vs. derivative 44
Distance from point to set 34
Divergence 263
Divergence theorem 319
Dominated by 139
Dot product 3
Dual basis 222
Dual space V* 220
Dual transformation of forms 267
Dual transformation of forms, calculation 269 273
Dual transformation of forms, properties 268
Dual transformation of tensors 224
Echelon form 8
Elementary 1-form 249 253
Elementary alternating tensor 232
Elementary alternating tensor as wedge product 237
Elementary k-form 249 254
Elementary k-tensor 221
Elementary matrix 11
Elementary permutation 227
Elementary row operation 8
Entry of matrix 4
Euclidean metric 25
Euclidean norm 4
Euclidean space 25
Even parametrization 228
Exact form 259
Expansion by cofactors 23
Ext A 29
Extended integral 121
Extended integral as limit of integrals 123 130
Extended integral as limit of series 141
Extended integral vs. ordinary integral 127 129 140
Extended integral, properties 125
Exterior 29
Extreme-value theorem 34
Face of rectangle 92
Final point of arc 306
FORM see “Differential form”
Frame 171
Fubini’s theorem for rectangles 100
Fubini’s theorem for simple regions 116
Fundamental theorem of calculus 98
Gauss — Jordan reduction 7
Gauss’ Theorem 319
Gradient 48 263
Gradient theorem 312
Gram — Schmidt process 180
Graph 97 114
Green’s Theorem 308
Half-ball 169
hemisphere 192
Homeomorphism 345
Homologically trivial 259
Homotopy equivalence 336
Homotopy equivalence theorem 336
Homotopy, differentiable 325
Homotopy, straight-line 331
Identity matrix 5
Implicit differentiation 71 73
Implicit function theorem 74
Improper integral 121
Increasing function 90
Independent 2 10
Induced orientation of boundary 288 307 346
Induced transformation of deRham group 335
Induced transformation of quotient space 335
Induced transformation of tangent vectors 246
Initial point of arc 306
Inner product 3
Inner product space 3
Int A 29
Integrable 85
Integrable, extended sense 121
Integral of constant 87
Integral of form on 0-manifold 307
Integral of form on differentiable manifold 353
Integral of form on manifold in  293—294 293—294
Integral of form on open set in 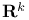 276 276
Integral of form on parametrized-manifold 276
Integral of max, min 105
Integral of scalar function over manifold 210 212
Integral of scalar function over parametrized-manifold 189
Integral of scalar function over Riemannian manifold 355
Integral of scalar function vs. integral of form 299
Integral over bounded set 104
Integral over bounded set, existence 109 111
Integral over bounded set, properties 106
Integral over interval 89
Integral over rectangle 85
Integral over rectangle, evaluation 102
Integral over rectangle, existence 93
Integral over rectifiable set 112
Integral over simple region 116
Integral, extended see “Extended integral”
Interior of manifold 205 346
Interior of set 29
Intermediate-value theorem 38
Invariance of domain 67
Inverse function theorem 69
Inverse function, derivative 60
Inverse function, differentiability 65
Inverse matrix 13
Inverse matrix, formula 22
Inversion in a permutation 228
Invertible matrix 13
Inward normal 318
Isolated point 27
Isometry 120 174
Isometry, preserves volume 176
Isomorphism, linear 6
Iterated integrals 103
Jacobian matrix 47
Jordan content 113
Jordan-measurable 113
k-form see “Form”
Klein bottle 285
Left half-line 283
Left inverse 12
Left-handed 171
Leibnitz notation 60
Leibnitz’s rule 324
Length 179
Length of interval 81
Length of parametrized-curve 191
Length of vector 4
Lie group 209
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



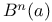
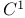
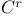
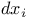 , elementary 1-form
, elementary 1-form 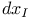 , elementary k-form
, elementary k-form 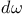 , differential
, differential 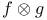 , tensor product
, tensor product 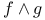 , wedge product
, wedge product 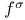
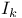 , identity matrix
, identity matrix 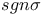
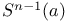
 , symmetric group
, symmetric group 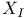 , submatrix
, submatrix 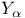
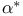 , dual transformation of forms
, dual transformation of forms 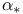 , induced transformation of vectors
, induced transformation of vectors  -neighborhood of point
-neighborhood of point 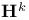 ,
, 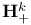
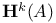 , deRham group
, deRham group 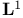 left half-line
left half-line  as metric space
as metric space 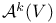 , alternating tensors
, alternating tensors 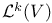 , k-tensors on V
, k-tensors on V 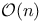 , orthogonal group
, orthogonal group 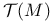
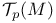
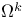 , linear space of k-forms
, linear space of k-forms 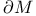
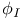 , elementary tensor
, elementary tensor 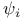 , elementary alternating tensor
, elementary alternating tensor 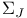
![$\Sigma_{[I]}$](/math_tex/d7b3d09d3509649f6bb51800910533d982.gif)
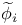 , elementary 1-form
, elementary 1-form 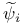 , elementary k-form
, elementary k-form