|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Munkres J.R. — Analysis on manifolds |
|
|
 |
| Предметный указатель |
LIMIT 28
Limit of composite 30
Limit point 26
Limit vs. continuity 29
Line integral 278
Line segment 39
linear combination 2
Linear in 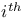 variable 220 variable 220
Linear isomorphism 6
Linear space 1
Linear space of k-forms 255
Linear subspace 2
Linear transformation 6
Linearity of integral of form 295
Linearity of integral of scalar function 213
Linearity of integral, extended 125
Linearity of integral, ordinary 106
Lipschitz condition 160
Locally bounded 133
Locally of class 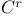 199 199
Lower integral 85
Lower sum 82
Manifold 200
Manifold of dimension 0 201
Manifold without boundary 196
Matrix 4
Matrix addition 4
Matrix cofactors 22
Matrix multiplication 5
Matrix, column 6
Matrix, elementary 11
Matrix, invertible 13
Matrix, non-singular 14
Matrix, row 6
Matrix, singular 14
Mayer — Vietoris theorem 337
Mean-value theorem in 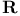 49 49
Mean-value theorem in 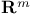 59 59
Mean-value theorem, second-order 52
Measure zero in  91 91
Measure zero in manifold 213
mesh 82
Metric 25
Metric space 25
Metric, Euclidean 25
Metric, Riemannian 354
Metric, sup 25
Minor 19
Mixed partials 52 103
Moebius band 285
Monotonicity of integral 106
Monotonicity of integral (extended) 125
Monotonicity of volume 112
Multilinear 220
Multiplication by scalar 1 4
Multiplication of matrices 5
n-1 sphere 207
n-1 sphere as manifold 208
n-1 sphere, volume 218
n-ball, 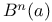 207 207
n-ball, 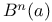 , as manifold 208 , as manifold 208
n-ball, 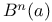 , volume 168 , volume 168
n-manifold see “Manifold”
Natural orientation of n-manifold 286
Natural orientation of tangent space 298
Neighborhood 26 (see also “ -neighborhood”) -neighborhood”)
Non-orientable manifold 281
Non-singular matrix 14
Norm 4
Normal field to n-1 manifold vs. orientation 285 312
Normal field to n-1 manifold, formula 314
Odd permutation 228
Open ball 26
Open covering 32
Open cube 26
Open rectangle 30
Open set 26
Opposite orientation of manifold 286 346
Opposite orientation of vector space 171
Order (of a form) 248
Orientable 281 346
Orientation for 0-manifold 307
Orientation for 1-manifold 282
Orientation for boundary 288
Orientation for manifold 281 346
Orientation for n-1 manifold 285 312
Orientation for n-manifold 286
Orientation for vector space 171 282
Orientation-preserving, diffeomorphism 281
Orientation-preserving, linear transformation 172
Orientation-reversing, diffeomorphism 281
Orientation-reversing, linear transformation 172
Oriented manifold 281 346
Orthogonal group 209
Orthogonal matrix 173
Orthogonal set 173
Orthogonal transformation 174
Orthonormal set 173
Oscillation 95
Outward normal 318
Overlap positively 281 346
Parallelopiped 170
Parallelopiped, volume 170 182
Parametrized-curve 48 191
Parametrized-manifold 188
Parametrized-manifold, volume 188
Parametrized-surface 191
Partial derivatives 46
Partial derivatives, equality of mixed 52 103
Partial derivatives, second-order 52
Partition of interval 81
Partition of rectangle 82
Partition of unity 139
Partition of unity on manifold 211 352
Peano curve 154
Permutation 227
| Permutation group 227
Poincare lemma 331
Polar coordinate transformation 54 148
Potential function 323
Preserves 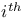 coordinate 156 coordinate 156
Primitive diffeomorphism 156
Product, matrix 5
Product, tensor see “Tensor product”
Product, wedge see “Wedge product”
Projection map 167
Pythagorean theorem for volume 184
Quotient space V/W 334
Rank of matrix 7
rectangle 29
Rectangle, open 30
Rectifiable set 112
Reduced echelon form 8
Refinement of partition 82
Restriction of coordinate patch 207
Restriction of form 337
Reverse orientation see “Opposite orientation”
Riemann condition 86
Riemann integral 89
Riemannian manifold 355
Riemannian metric 354
Right inverse 12
Right-hand rule 172
Right-handed 171
Row index 4
Row matrix 6
Row operations 8
Row rank 7
Row space 7
Scalar field 48 251
Sign of permutation 228
Simple region 114
Singular matrix 14
Size of matrix 4
Skew-symmetric 265
Solid torus 151
Solid torus as manifold 208
Solid torus, volume 151
span 2 10
Sphere see “n-1 sphere”
Spherical coordinate transformation 55 150
Stairstep form 8
Standard basis 3
Star-convex 330
Stokes’ theorem for 1-manifold 308
Stokes’ theorem for arc 306
Stokes’ theorem for differentiable manifold 353
Stokes’ theorem for k-manifold in  303 303
Stokes’ theorem for surface in  319 319
Straight-line homotopy 331
Subinterval determined by partition 82
Subrectangle determined by partition 82
Subspace of metric space 25
Subspace, linear 2
Substitution rule 144
Sup metric 25
Sup norm for matrices 5
Sup norm for vectors 4
Support 139
Symmetric group 227
Symmetric set 168
Symmetric tensor 229
T* see “Dual transformation of tensors”
Tangent bundle 248
Tangent space to  245 245
Tangent space to manifold 247 349
Tangent vector field to  247 247
Tangent vector field to manifold 248
Tangent vector to  245 245
Tangent vector to manifold 247 348 351
Tensor 220
Tensor field on manifold 249
Tensor field to  248 248
Tensor product 223
Tensor product, properties 224
Topological property 27
Torus 151
Torus as manifold 208
Torus, area 217
Total volume of rectangles 91
Transition function 203 346
TRANSPOSE 9
triangle 193
Triangle inequality 4
Uniform continuity 36
Upper half-space 200
Upper integral 85
Upper sum 82
Usual basis for tangent space 249
V(X), volume function 181
V*, dual space 220
V/W, quotient space 334
Vector 1
Vector addition 1
Vector space 1
Velocity vector 48 245 349
Volume form 300
Volume form for Riemannian manifold 355
Volume of 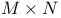 218 218
Volume of bounded set 112
Volume of cone 168
Volume of manifold 212
Volume of n-bail 168
Volume of n-sphere 218
Volume of parallelopiped 182
Volume of parametrized-manifold 188
Volume of rectangle 81
Volume of Riemannian manifold 355
Volume of solid torus 151
Wedge product, definition 238
Wedge product, properties 237
width 81
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



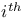 variable
variable 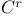
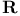
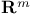

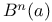
 -neighborhood”)
-neighborhood”)