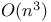|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lawler E.L. — Combinatorial Optimization: Networks and Matroids |
|
|
 |
| Предметный указатель |
Multicommodity flows, synthesis problem 176
Multigraph 25
Multiplier, path 136
Multiterminal flows 173—176
Multiterminal flows, analysis problem 174
Multiterminal flows, synthesis problem 175
Munro, I. 106
Murchland, J.D. 355
Murty, K.G. 107
Nash-Williams, C.St.J.A. 317 318 353
Negative cycles 90 131
Nemhauser, G. 12
Network synthesis problem, generalized 361
Ninomiya, K. 261
Node 20
Node covering problem 8
Norman, R.Z. 222 226 262
NP-complete 8
Objective function, linear programming 41
Oettli, W. 178
Onaga, K. 179
Open path 26
Orden, A. 181
Ore, O. 58
Orthogonalility, dual solution 56
Out-degree 24
Out-of-kilter method, linear programming 57
Out-of-kilter method, network 142—156
Out-of-kilter method, theoretical improvement 157—159
Painting theorem 32
Painting theorem, applied 145
Palermo, F.P. 299
Parity problem, matroid 356
Partial transversal 183
Partition matroid 272
Path 26
PERT networks 61
PERT scheduling 165—169
Philip Hall theorem 323
Pivot element, linear programming 44
Planar graph 32
Plane graph 33
Pollak, H.O. 299
Polynomial bounded 5—8
Potts, R.B. 208 216
Prager, W. 178 180
Prim, R.G. 285 299
Primal algorithm, weighted matroid intersection 333
Primal-dual algorithm, linear programming 57
Primal-dual algorithm, weighted matroid intersection 345—347
Project scheduling 165—169
Provisioning problem 125
Pseudonode, directed spanning tree 349—351
Pseudonode, nonbipartite matching 230
Rabin, M.O. 222 226 262
Rado, R. 276
Rao, M.R. 107
Ratio test, linear programming 46
Reiter 707
Relations 16
Relaxation procedure, shortest path 77—82
Reliable paths 61
Renumbering nodes 30
Restricted satisfiability problem 2
Rhys, J. 178
Robbins, H. 299
Romanovskii, I.V. 107
Root, nonbipartite matching 229
Rosenstiehl, P. 284 298
Rota, G.-C. 296
Roy, B. 58 180
Ryser, H.J. 12
Saaty, T.L. 12 177
Salkin, H.M. 12
Satisfiability problem 9
Scheduling problem, two processor 218
School busing problem 208
Secondary variables, linear programming 41
Semimatching problem 265 278
Separating set 31
Sequencing problem 265 278
Sequencing problem, generalized 360
Set 16
Set, maximal 17
Set, minimal 17
Shannon switching game 324—326
| Shannon, C.E. 177 354
Shapley, L.S. 211 212 216
Shortest path algorithm, acyclic 68 72
Shortest path algorithm, Bellman — Ford 74
Shortest path algorithm, Dijkstra 71
Shortest path algorithm, Floyd — Warshall 86—90
Shortest path algorithm, relaxation 79
Shortest path algorithm, Yen 76
Shortest path problem 2 143
Shortest path problem, all pairs 82—85
Shortest path problem, reduction to assignment problem 186
Shortest path problem, undirected 220
Shortest path tree 66
Simonnard, M. 58
Simple border graph 309
Simplex method 43—47
Sink node 109
Skies and skiers problem 208
source node 109
Span, matroid 269
Spanning tree 2 27
Spanning tree, radially symmetric 360
Spira, P. 73 106
Stairs, S.W. 104
Statistical sampling methods 10 12
Steiner network, problem 8 290—296
Stem, nonbipartite matching 229
Stepanets, G.F. 298
Strassen, V. 105
Strong component 28
Strong duality theorem 56
Symmetric bipartite matching problem 219
Symmetric difference 16
System of distinct representatives 183
Takamori, H. 200 216
Takata, M. 179
Tarjan, R.E. 299 354 355
Terminal nodes, 35
Thrall, R.M. 58
Threshold method 198—199
Tomijawa, N. 354
Total unimodularity 160—165
Tramp steamer problem 62
Transhipment problem 169—172
Transit times, arc 92—94
Transportation problem 169—172
Transversal 183
Transversal matroid 272
Traveling salesman problem 9 63 304
Tree, defined 27
Tree, shortest path 66
Truemper, K. 179
Turner, J. 298
Tutte, W.T. 241 263 296 297 353
Twenty questions problem 2
Unimodular matrix 160
Urquhart, R.J. 263
Valkenburg, M.E. 179
Veinott, A.F. 161 180
Vieducts, G.E. 298
Vilenkin, N.Ya. 12
von Randow, R. 297
Wagner, H.W. 181
Wagner, R.A. 294 299
Walker, M.R. 180
Warshall, S. 106
Weak duality theorem 55
Weighted augmenting sequences 326
Weighted matching algorithm, nonbipartite, 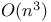 256 256
Weighted matching algorithm, nonbipartite,  251 251
Weighted matching algorithm, nonbipartite, summary 246
Weighted matching problem, bipartite 183
Weighted matching problem, linear programming formulation 242
Weinberg, L. 325 354
Wells, M.B. 12
Welsh, D.J.A. 297 353
White, L.J. 263
Whitney, H. 264 274 275 296
Wilson, R.J. 58
Witzgall, C. 262
Work assignment problem 135
Yakovleva, M.A. 180
Yamada, H. 106
Yao, A.C.-C. 299
Yen, J.Y. 76 105 108
Zadeh, N. 119 177
Zahn, C.T., Jr. 262
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте