|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Berry D.A., Fristedt B. — Bandit problems |
|
|
 |
| Предметный указатель |
 -metric 24 -metric 24
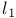 -norm 24 -norm 24
Abdel Hamid, A.R. 207
Adaptive reinvestment 236
Admissible strategy see “Strategy admissible”
Advantage of an arm 70 151 152
Anscombe, F.J. 208 211 219 221 222 223 233 241 243
Antle, C.E. 3 8 210 227 242 255
ARM 1
Arm, advantage of 70
Arm, definition of 9
Arm, infinitely many 242
Arm, optimal 2 4 17 27 70 227
Arm, risky 61 214
Armitage, P. 208
Asano, C. 221 231
Asymptotic optimality 208—211 221 222 227 229 232 234 238 241—243 247—249 251 254—258 260
Backwards induction see “Dynamic programming”
Bandit 1 11 17 62 223
Bandit with a goal 213 214
Bandit, arm-acquiring 224 250 255
Bandit, continuous-time 7 131 166 179
Bandit, discrete-time 192
Bandit, finite-memory 3 7 207 222 223 231 241 242 248 249 251 256 257
Bandit, finite-state 202 231 257
Bandit, quasi- 139
Barnett, B.N. 3 7 63 64
Bather, J.A. viii 178 189 197 201 206 209 210 211 213 220 221 228 229 230 242 243 245 247 250 252 254 259
Bayesian approach 2 4 191 208 210
Beckmann, M.J. 211 225 230 231
Begg, C. 8 211 219 221 241 246
Bellman, R. 2 7 86 88 134 210 212 213 227 228 229 240 251 257 259
Benzig, H. 212 231 232 239 240
Berger, J. 0 135
Bernoulli arm 211—224 28 30 34 35 36 37 38 65 82 107 129 134 142 150 192 209—219 223—226 228—240 243—245 247—249 251—256 259 260
Bernoulli arm, moments of 72
Berry, D.A. 50 64 73 82 88 90 92 99 107 125 128 129 131 134 150 165 210 212 213 214 215 217 218 220 221 223 224 225 228 233 234 235 236 238 239 240 245 248 252 253 254 255 256 259 260
Beta distribution 3 74 126 153 158 161 213 228 229 234 235 240 244 245 247 250 255
Blackwell, D. 236
Borel field 13—15
Borel subset 10 13 16 53 169
Boundary function 175
Bradt, R.N. 2 3 7 28 49 86 88 92 114 134 155 165 207 210 212 213 215 220 223 225 235 237 239 240 248 257 259
Brand, H. 215 216 217 244 259
Break-even observation 128
Break-even value of a known arm 39 86 100 107 123 127 133 172 210 212 227—229 238 250 255 256
Break-even value, calculation of 39 107 113 114 129 219 238
Break-even value, continuity of 101
Break-even value, effect of failure on 104
Break-even value, effect of success on see “Staying with a winner”
Break-even value, existence of 86 100 123 133
Break-even value, formula for 101
Break-even value, graph of 109 110
Break-even value, lower bounds for 110 240
Break-even value, monotonicity of 87 102
Break-even value, upper bound for 114 240
Breakwell, J. 175 178 189 211 216 220
Brownian arm 167 175 182 184 185 201 210 218 220
Brownian motion 167 168 170—175 182 202 210 218
Bush, R.R. 216 217 232 233 244 251
Buyukkoc, C. 228 230 249 253 255 256
Cane, V.R. 217 251
Canner, P.L. 208 217 221 238 244 260
Cardiac arrhythmias 260
Chandrasekaran, B. 222 241 249
Chernoff, H. 167 175 178 179 189 211 216 217 218 219 220 221 227 246
Chow, Y.S. 20 49 258
Christensen, R. 134
Chung, F. 220
Classical statistical tests 208 221 233
Clayton, M.K. viii 63 125 128 131 134 220
Clinical trial 1 5 51 59 63 208 211 213 214 218—221 223 225 226 229 231 232 240 241 244—246 253 259
Colton, T. 207 208 209 211 215 218 219 220 221 222 223 226 227 231 232 238 241 242 243 244 245 246 249 253 254 255 260 261
complete 14 15
Computational technique, numerical 47 114
Computer program 114
Concomitant variable 258
Conjecture of Berry 164 165 235 236
Conjecture of Chernoff 218 227
Conjecture of Clayton and Berry 131
Conserving selection 45
Continuity of  101 101
Continuity of V 40 42 66 83
Continuity of W 45
Continuous time 7 59 218 246 247 253
Continuous-time approximation 83 219 220 242 246
Convergence in distribution 13 14 15 19 53
Cornfield, J. 208 221 222 260
Cost of switching 167 239
Counter example to continuity of V 42 56
Counter example to monotonicity of  36 36
Counter example to monotonicity of  in in 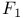 80 80
Counter example to monotonicity of  in in  87 87
Counter example to optimality of myopic strategy 4 30 34 215
Counter example to optimality of staying with a known arm 89 90
Counter example to optimality of staying with a winner 28
Counter example to optimality of staying with the known arm 89 90
Counter example to transitivity of preference among arms 137
Cover, T.M. 222 249
Cox, T.F. 230
Day, N.E. 221 223
DeGroot, M.H. 11 12 49 80 82 223 225 238 250 260
Delayed information 225 241 250
Dellacherie, C. 181 190
Dempster, M.A.H. 228
Dependent arms 28 65 81 212 222 224 232 238 240 243 247 248 250 251 255
Diffusion 174 177 210 238
Dirichlet measure 85 125 220
discount factor 1 225
Discount factor, nonobservable 53
Discount factor, observable 55
Discount function 60 131 180
Discount function, exponential 60 131 134 167 185 202 210 238
Discount function, regular 132
Discount function, shifted 132
Discount function, uniform 60 134 175 218—220
Discount sequence, condition for regularity 90
Discount sequence, definition of 9
Discount sequence, finite horizon 4
Discount sequence, geometric 2 5 6 47 50 51 54 91 107 108 113 115 117 120 136 197 212 215 218 223—225 227—231 235—241 244 250 251 253 255—259
Discount sequence, mixture of 51
Discount sequence, mixture of geometrics 54
Discount sequence, monotone 76 85
Discount sequence, nonmonotone 63
Discount sequence, norm of 24
Discount sequence, random 6 50 213 253 256
Discount sequence, random equivalent to nonrandom 54
Discount sequence, regular 90 99 111 120
Discount sequence, role of 50
Discount sequence, space of 24
Discount sequence, superregular 90 214
Discount sequence, topology for 24
Discount sequence, topology for random 53
Discount sequence, truncated geometric 235 239 250
Discount sequence, uniform 2—4 9 50 54 91 108 113 119 126 136 150 175 199 209 212—15 217—219 221 223—27 232—45 247—50 252—55 259
Discount sequence, unknown 50
Discrete-time approximation 61 134 175 219
Dose response 260
Drift process, deterministic 167 175
Drift process, random 167 175 220
Dubins, L.E. 19 45 49 223 225
Dynamic allocation index see “Break-even value of a known arm”
Dynamic programming 4 6 9 25 36 46 114 212 219 224 233 235 248 252
Dynamic programming, advantages 106
Dynamic programming, disadvantages 106
Dynamic programming, fundamental equation of 27
Eick, S.G. viii 20 36 49
Electronic device 216 243
Emrich, L.J. 224
Equal allocation 208 211 223 226 238 243—245 254 260
| Estes, W.K. 216 217 224 233 244
Excessivity 223
Experimental phase 208 211 217 219 221—223 226 231 241 244 245 254—256 260
Exponential arm 225 227 229 232
Fabius, J. 81 82 210 211 224 225 231 238 242 250 254 260
Fahrenholtz, S.K. 224
Feldman, D. 2 4 7 80 81 82 210 214 215 219 222 223 224 225 238 240 243 245 248 250 254 255 259 260
Feller, W. 198 206
Ferguson, T.S. viii 85 125 126 135
Finite horizon 2 9 24
Fischer, J. 225 230 231 240
Fisk, G. 243
Flehinger, B.J. 221 225 226 242 249
Fox, B.L. 209 210 221 226 227 245 249 250 253 255
Free boundary problem 178 217 220
Freedman, D. 19 49
Fristedt, B. 88 90 92 99 107 134 171 190 202 206 210 212 213 214 215 220 223 228 234 235 237 240 253 254 259
Fu, K.S. 222
Furukawa, N. 227
Gait, P.A. 227
Gambling, fundamental theorem, of 225
Game-theoretic approach 191
Gani, J. 7 135 149 228
Generator 174
Gittins index see “Break-even value of a known arm”
Gittins — Jones theorem 6 139 227 228 230 238 244 249 250 253 255 256
Gittins — Jones theorem, converse to 145
Gittins, J.C. vi viii 6 7 85 86 135 136 137 138 145 149 210 211 212 213 214 218 224 227 228 229 230 235 238 239 244 249 250 251 253 254 255 256 259
Glazebrook, K.D. 210 225 228 229 230 240 249 255 256
Goto, M. 221 231
Gray, K.B.Jr. 231 248
Greenhouse, S.W. 208 221 222 260
Gupta, S. 135
Halperin, M. 208 221 222 260
Hamada, T. 231
Heath, D.C. viii 182 190
Hellman, M.E. 222 249
Hengartner, W. 63 212 240
Herkenrath, U. 63 210 213 228 230 231 232 235 243 257
Hill, C. 232
Hinderer, K. 212 231 232 240
History of observations 1 4 10 16 62
Horizon 2 9 50 208
Horizon, definition of 24
Horizon, equals two 152
Horowitz, A.D. 216 217 233 244
Improper prior 13 156
Independent arms 65 136 150
Independent increments 179
Infinite horizon 9
Infinitely divisible 179
information 2 5 7 10 11 15 63 154 179 225 241 250
Inter-arrival time 60
Iosifescu, M. 233
Isbell, J.R. 3 7 233 249 251 252
Isoptin 260
Ito's formula 173
Ito, K. 247
Jain, N.C. viii 49
Job seleCtion 253
Johnson, N.L. 213 252
Johnson, S.M. 2 3 7 28 49 86 88 92 114 134 155 165 207 210 212 213 215 220 223 225 235 237 239 240 244 249 250 251 253 255 256 259
Jones, D.M. vi viii 6 7 85 86 135 136 137 138 145 149 211 212 213 225 227 228 229 230 234 235 238 239
Jones, P.W. 234 235 237 245
Joshi, V.M. 164 165 235 236
Kadane, J.B. 81 82
Kakigi, R. 212 236
Kalaba, R.E. 236 252
Kalin, D. 63 210 212 213 228 230 231 235 236 237 240 243 257
Kandeel, H.A. 234 235 237 245
Karatzas, I. 174 185 90 211 238
Karlin, S. 2 3 7 28 49 86 88 92 114 134 155 165 207 210 212 213 215 220 223 225 235 237 239 240 248 257 259
Keener, R.W. 238 248 250
Kelley, T.A. 81 82 218 221 223 225 238 239 247 250 260
Kelly, F.P. 210 238 258
Kemperman, J.H.B. 248
Klimko, L.A. 3 8 210 227 242 255
Known arm 4 6 9 38 83 168 186 209 210 212—215 218 220 223 225 227 230 231 234 235 237 239 240 242 245 253 256—259
Known arm, staying with see “Stopping problem”
Kolonko, M. 212 231 232 239 240
Kono, K. 240
Kotz, S. 213 252
Kumar, P.R. 240
Ladder epochs of random walks 238
Lai, T.L. 208 221 240 241
Lakshmanan, K.B. 241 249
Lakshmivarahan, S. 242 249
Langenberg, P. 221 249
Learning models 224 232 242 251 259
Learning models, linear 217 233
Learning models, nonlinear 233
Least-failures rule 239
Lee, R.D. 208 221 253
Lellouch, J. 221 244 245
Lenstra, J.K. 228
Levin, B. 221 240 241
Levy arm 179 184 186
Levy measure 186—188
Levy process 7 167 168 179—181 183 184 186 189
Likelihood ratio test 226 249
Lindley, D.V. 63 64
Lipster, A.S. 174 190
Locally compact 14 15
Louis, T.A. 221 225 226 242 249
m-Decreasing, definition of 76
m-Decreasing, strictly 76
m-Greater than 73 159
m-Increasing, definition of 76
m-Increasing, strictly 76
Mallows, C.I. 242
Market pricing problem 232 251
Markov environment 257
Markov process 177 228 254
Markov property 173
Maximin strategy 193 199 202 206
Maximizing length of success run 214 215
Maximum principle of Pontryagin 246
McCulloch, R.E. viii
Medical ethics 208 219 233 244 245
Medical trials see “Clinical trials”
Meeter, D.A. 221 242 255
Mehta, C.R. 211 219 221 241 246
Metrizable 14 15
Meybodi, M.R. 242 249
Meyer, P.-A. 181 190
Minimax approach 3 7 191 254
Minimax risk 210 211
Minimax strategy 193 196 202 206 210—211 217 224 251 253 254
Minimizing selections on an inferior arm 225 226 245 249 260
Mixed strategy 192 196 207 209 210 224 229 232 233 241 243 247 248 251—253
Monotonicity of A 86
Monotonicity of V 66 69 75 83
Monotonicity, of  36 98 36 98
Monotonicity, of  76 86 76 86
Monotonicity, of  10 129 10 129
Monte Carlo 226 252
Morrison, D.F. 243
Mosteller, F. 216 217 223 232 233 244 251
Multi-phase design 222 243 256
Murray, F.S. 216 217 243
Myopic strategy 4 34 213—215 223—225 233—235 238 243—245 248 250 252 255 258 259 260
Nakajima, N. 244
Nash, P. 229 244 256
Ney, P. 190 206
Nonparametric arm 125 220
Nordbrock, E. 79 82
Normal arm 10 15 23 221 223 224 242 243 249 258
Normal distribution 10 24 129 175 179 220 224 258
Noshi, T. 244
Number of immediate failures tolerated 218
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -metric
-metric 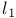 -norm
-norm 

 in
in